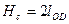Расчет производиться с целью определить основные размеры кривошипно-шатунного механизма, определить момент инерции маховых масс обеспечивающий заданную неравномерность хода. Используется метод моделирования системы одномассной моделью. В качестве звена приведения принимается коленчатый вал двигателя (кривошип 1).
Определение основных размеров механизма.
Для того чтоб сделать возможным дальнейший кинематический расчет необходимо определить основные размеры механизма по заданным параметрам (средняя скорость поршня на холостом ходу и количество оборотов коленчатого вала на холостом ходу).
Определяется время одного оборота Т.
|
Ход поршня равняется удвоенной длине кривошипа.
|
Используя определение средней скорости производиться определение длины кривошипа.
|
По заданной относительной длине определяется длина шатуна.
|
Аналогично получаем  и
и 
Определение площадей поршней.
Находим площадь поршней Sпоршня = π*d2поршня/4 =0,005 м2.
Построение индикаторных диаграмм.
.
Индикаторные диаграммы строим по данным таб. 1.1 значений давлений в цилиндрах двигателя. mp=8 мм/105 Па, mF=8 мм/К
Таблица 1.1
| Путь поршня (в долях от Н) | SB/H | 0,05 | 0,1 | 0,2 | 0,3 | |
| Всасывание | 0,02 | -0,02 | -0,02 | -0,02 | -0,02 | |
| Сжатие | p/(pmax)xx | 0,57 | 0,41 | 0,30 | 0,18 | 0,12 |
| Расширение | 0,57 | 0,85 | 0,66 | 0,43 | 0,31 | |
| Выхлоп | 0,02 | 0,02 | 0,02 | 0,02 | 0,02 |
| Путь поршня (в долях от Н) | SB/H | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| Всасывание | -0,2 | -0,2 | -0,2 | -0,2 | -0,2 | -0,2 | -0,2 | |
| Сжатие | p/(pmax)xx | 0,083 | 0,053 | 0,028 | 0,008 | -0,01 | -0,019 | -0,02 |
| Расширение | 0,23 | 0,14 | 0,115 | 0,095 | 0,066 | 0,03 | ||
| Выхлоп | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,2 | 0,3 |
Построение графиков аналогов скоростей и передаточных функций.
Из программы AR2 получаем данные (таблица 1.2),по которым строим графики передаточных функций и аналогов скоростей.
Таблица 1.2
| F˚i0 | Vq3 | U q2 | J сум | J 3 | J 2 | J2 вр | J 2 пос |
| -0,00000 | -0,26316 | 0,000405 | 0,000000 | 0,000405 | 0,000139 | 0,000267 | |
| -0,01299 | -0,25478 | 0,000482 | 0,000061 | 0,000421 | 0,000130 | 0,000291 | |
| -0,02459 | -0,22990 | 0,000679 | 0,00218 | 0,000461 | 0,000106 | 0,000355 | |
| -0,03364 | -0,18939 | 0,000916 | 0,000407 | 0,000509 | 0,000072 | 0,000437 | |
| -0,03932 | -0,13513 | 0,001102 | 0,000557 | 0,000545 | 0,000037 | 0,000508 | |
| -0,04136 | -0,07042 | 0,001173 | 0,000616 | 0,000557 | 0,000010 | 0,000547 | |
| -0,04000 | 0,00000 | 0,001120 | 0,000576 | 0,000544 | 0,000000 | 0,000544 | |
| -0,03591 | 0,07042 | 0,000979 | 0,000464 | 0,000514 | 0,000010 | 0,000504 | |
| -0,02996 | 0,13513 | 0,000802 | 0,000323 | 0,000479 | 0,000037 | 0,000442 | |
| -0,02293 | 0,18939 | 0,000636 | 0,000189 | 0,000447 | 0,000072 | 0,000375 | |
| -0,01540 | 0,22990 | 0,000509 | 0,000085 | 0,000424 | 0,000106 | 0,000318 | |
| -0,00771 | 0,25478 | 0,000431 | 0,000021 | 0,000410 | 0,000130 | 0,000280 | |
| -0,00000 | 0,26316 | 0,000405 | 0,000000 | 0,000405 | 0,000139 | 0,000267 | |
| 0,00771 | 0,25478 | 0,000431 | 0,000021 | 0,000410 | 0,000130 | 0,000280 | |
| 0,01540 | 0,22990 | 0,000509 | 0,000085 | 0,000424 | 0,000106 | 0,000318 | |
| 0,02293 | 0,18939 | 0,000636 | 0,000189 | 0,000447 | 0,000072 | 0,000375 | |
| 0,02996 | 0,13513 | 0,000802 | 0,000323 | 0,000479 | 0,000037 | 0,000442 | |
| 0,03591 | 0,07042 | 0,000979 | 0,000464 | 0,000514 | 0,000010 | 0,000504 | |
| 0,04000 | 0,00000 | 0,001120 | 0,000576 | 0,000544 | 0,000000 | 0,000544 | |
| 0,04136 | -0,07042 | 0,001173 | 0,000616 | 0,000557 | 0,000010 | 0,000547 | |
| 0,03932 | -0,13513 | 0,001102 | 0,000557 | 0,000545 | 0,000037 | 0,000508 | |
| 0,03364 | -0,18939 | 0,000916 | 0,000407 | 0,000509 | 0,000072 | 0,000437 | |
| 0,02459 | -0,22990 | 0,000679 | 0,00218 | 0,000461 | 0,000106 | 0,000355 | |
| 0,01299 | -0,25478 | 0,000482 | 0,000061 | 0,000421 | 0,000130 | 0,000291 |
Построение графиков приведенного момента инерции II группы звеньев.
Воспользовались методом приведения масс.
В основу метода приведения масс положено условие равенства кинетической энергии всех звеньев механизма и звена динамической модели. В этом случае закон движения последнего будет таким же, как и закон движения начального звена реального механизма.
Для определения приведенного момента инерции 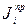 каждого звена механизма составили равенство кинетических энергий рассматриваемого звена и звена модели.
каждого звена механизма составили равенство кинетических энергий рассматриваемого звена и звена модели.
В зависимости от характера движения звена существуют следующие варианты равенстве кинетических энергий:
При поступательном движении i-го звена механизма
 ,
,
откуда
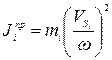
При вращательном движении звена вокруг неподвижной оси
 ,
,
откуда

При плоскопараллельном движении звена
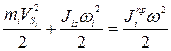
откуда

где  ,
,  - передаточные функции.
- передаточные функции.
Суммарный приведенный момент инерции всего механизма равен сумме приведенных моментов инерции всех его звеньев и зависит от положения механизма:

 зависит от отношения скоростей и может определяться без учета действительного закона движения звеньев.
зависит от отношения скоростей и может определяться без учета действительного закона движения звеньев.
Расчеты, полученные из программы AR 2,приведены в таблице 1.2
Масштаб графиков mJ=200000 мм/кг*м2.