1. Понятие и способы задания функций одной действительной переменной. Сложная и элементарная функции. Функции, заданные неявно, параметрически, кусочно, степенно-показательная. Примеры. Примеры основных элементарных функций.
2. Основные свойства функции: четность, ограниченность функции периодичность. Определения, примеры. Обзор свойств основных элементарных функций.
3. Графическое понятие предела функции в точке. Теорема о пределе элементарной функции. Основные свойства конечных пределов функции в точке. Примеры применения свойств.
4. Определение и свойства бесконечно малой функции в точке. Примеры применения свойств. Раскрытие неопределенности 
для дробно-рациональных функций. Пример.
5. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Доказательство какого-либо соотношения эквивалентности для двух функций.
6. Графическое понятие и свойства бесконечно большой функции в точке. Обзор бесконечно больших в точке основных элементарных функций. Примеры применения свойств для отыскания предела в точке.
7. Графическое понятие и свойства предела функции на бесконечности. Обзор пределов основных элементарных функций на бесконечности. Примеры применения свойств для отыскания предела на бесконечности.
8. Графическое понятие и свойства бесконечно большой функции на бесконечности. Раскрытие неопределенности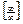 
для многочленов и 
.
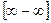9. Замечательные пределы. Примеры применения замечательных пределов при раскрытии неопределенностей и 
с использованием замены переменной.
10. Определение непрерывной функции в точке. Классификация точек разрыва. Графические иллюстрации. Примеры функций с точками разрывов первого и второго рода.
11. Определение непрерывной функции на множестве. Непрерывность элементарной функции. Пример исследования на непрерывность кусочно заданной функции. Обзор нарушений непрерывности основных элементарных функций.
12. Теоремы о непрерывных на отрезке функциях (о промежуточных значениях, Больцано-Коши, Вейерштрасса). Графические иллюстрации выполнения и невыполнения условий теорем.
13. Понятие асимптоты графика функции. Теоремы об условиях наличия вертикальной, горизонтальной и наклонной асимптот. Обзор наличия асимптот у основных элементарных функций.
14. Определение производной функции в точке. Доказательство формулы из таблицы производной по определению (на выбор: для синуса, косинуса, тангенса, показательной функции).
15. Правила дифференцирования. Производная сложной функции, пример. Производные для функций, заданных кусочно, неявно, параметрически (примеры).
16. Логарифмическое дифференцирование. Применение к степенно-показательной функции в общем виде. Пример дифференцирования дробно-иррациональной функции.
17. Непрерывность и дифференцируемость функции. Примеры функций, которые обладают одним свойством без другого. Правило Лопиталя. Примеры применения правила к раскрытию неопределенностей 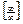для дробно-рациональных функций с бесконечным, конечным и нулевым пределами.
18. Определение дифференциала функции. Дифференциал и приращение аргумента. Инвариантность формы дифференциала. Внесение постоянных под знак дифференциала.
Приближенные вычисления с помощью дифференциала. Вывод формулы.
19. Геометрический смысл производной и дифференциала. Графические иллюстрации.
20. Производные и дифференциалы высших порядков. Выражение дифференциала высшего порядка через производную. Вывод формулы для дифференциала второго порядка.
21. Понятие монотонной на промежутке функции, точки экстремума и экстремумы. Исследование функции на монотонность и экстремумы: критические точки, теоремы о производной в точках экстремумов, о знаках производной и монотонности.
22. Выпуклая и вогнутая функция на промежутке. Точка перегиба графика функции. Исследование функции на выпуклость и наличие точек перегиба: критические точки второго рода, теоремы о второй производной в точках перегиба, о знаках второй производной и выпуклости.
23. Наибольшее и наименьшее значения функции на отрезке и интервале. Графические иллюстрации. Пример решения задачи с практическим содержанием.
24. Первообразная функция и неопределенный интеграл. Свойства неопределенного интеграла (вывод формул). Инвариантность формы неопределенного интеграла. Пример интегрирования путем внесения постоянных под знак дифференциала.
25. Интегрирование по частям в неопределенном интеграле. Вывод формулы. Рекомендации по выбору частей для специальных случаев.
26. Использование подстановки в неопределенном интеграле для сложной, тригонометрической, иррациональной функции. Примеры применения.
27. Интегрирование простейших рациональных дробей.
28. Определение и условия существования определенного интеграла. Свойства и вычисление определенного интеграла: формула Ньютона-Лейбница, особенности замены переменной, интегрирования по частям.
29. Геометрический смысл и приложения определенного интеграла. Использование полярных координат.
30. Интеграл с переменным верхним (нижним) пределом. Несобственный интеграл первого рода, его сходимость и геометрический смысл.
31. Функция нескольких переменных, ее область определения и способы задания. График функции двух переменных и его изображение.
32. Частные приращения функции двух переменных. Частные производные функции двух переменных. Производные высших порядков функции двух переменных.
33. Полное приращение и полный дифференциал функции двух переменных. Дифференциалы высших порядков. Выражение дифференциала второго порядка через производные (вывод формулы).
34. Производная по направлению и ее смысл.
35. Исследование функции двух переменных на экстремумы: критические точки, теоремы о производной в точках экстремумов, достаточное условие экстремума.
36. Интегральная сумма для функции двух переменных в области. Двойной интеграл, условия его существования и свойства.
37. Вычисление двойного интеграла путем сведения к повторному интегрированию: формулы для простых областей. Переход к полярным координатам.
38. Геометрические и физические приложения двойного интеграла.
На экзамене разрешается пользоваться: вопросами к экзамену, классификатором основных элементарных функций. При себе иметь чистую бумагу для подготовки к ответу.