Задание № 2
«Текстовые задачи»
При решении текстовых задач следует придерживаться следующих шагов:
1) читаем задачу,
2) неизвестные величины обозначаем буквами,
3) снова читаем задачу по частям и составляем, следуя условиям задачи, уравнения (либо неравенства) или их системы,
4) решаем полученные уравнения (либо неравенства) или их системы (лишние буквы при этом сократятся, их не надо бояться).
Задачи на проценты
(1% от числа x) =  ; (r % от числа x) =
; (r % от числа x) = 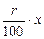 ;
;
Обозначим  . Число
. Число  называется долей или удельным процентом. Доля
называется долей или удельным процентом. Доля  от числа
от числа  равна
равна 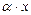 . Откуда
. Откуда 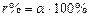 .
.
1. Если число  увеличить на
увеличить на  , т.е. на долю
, т.е. на долю  , то получится новое число
, то получится новое число  . Т.о., число
. Т.о., число  увеличилось в
увеличилось в  раз. Если новое число
раз. Если новое число  еще раз увеличить на долю
еще раз увеличить на долю  , то получится число
, то получится число  .
.
Если  , то
, то  .
.
Если процесс увеличения все новой накопленной суммы совершается  раз на одну и ту же долю
раз на одну и ту же долю  , то получим
, то получим
формулу сложных процентов:  .
.
Мы видим, что в формуле сложных процентов последовательность растет как геометрическая прогрессия со знаменателем 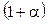 .
.
Например, так происходит начисление банковских процентов, когда проценты капитализируются, т.е. один и тот же процент начисляется, к примеру, ежегодно на накопленную сумму. Тогда положив сумму  , мы через
, мы через  лет получим сумму
лет получим сумму  .
.
2. Простой процент начисляется только на исходное число, т.е.  получим
получим
формулу простых процентов:  .
.
Мы видим, что в формуле простых процентов последовательность растет как арифметическая прогрессия с разностью 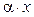 .
.
3. Если число  уменьшается на
уменьшается на  , т.е. на долю
, т.е. на долю  , то получается новое число
, то получается новое число  . Т.о., число
. Т.о., число  умножилось на
умножилось на  . Если новое число
. Если новое число  еще раз уменьшить на долю
еще раз уменьшить на долю  , то получим число
, то получим число  . Если
. Если  , то
, то  . Если процесс уменьшения совершается
. Если процесс уменьшения совершается  раз на одну и ту же долю
раз на одну и ту же долю  , то получим формулу:
, то получим формулу:  .
.
Например, так происходят амортизационные отчисления на капитальные вложения в оборудование, когда ежегодно списывается доля  от остаточной стоимости. Тогда если исходная стоимость была равна
от остаточной стоимости. Тогда если исходная стоимость была равна  д.е., то через
д.е., то через  лет она станет равной
лет она станет равной  .
.
Задача. Имеется  (л) раствора кислоты концентрации
(л) раствора кислоты концентрации  (в долях). Проделаем
(в долях). Проделаем  раз следующую процедуру: отольем
раз следующую процедуру: отольем  (л) раствора (т.е. долю
(л) раствора (т.е. долю  ) и дольем чистой воды до объема
) и дольем чистой воды до объема  . Требуется определить концентрацию получившегося в результате раствора.
. Требуется определить концентрацию получившегося в результате раствора.
Решение: Количество чистой кислоты в растворе равно  (л). После одного отливания останется
(л). После одного отливания останется  (л) чистой кислоты. Тогда концентрация нового раствора после добавления
(л) чистой кислоты. Тогда концентрация нового раствора после добавления  (л) воды станет равной
(л) воды станет равной  . Аналогично, после
. Аналогично, после  таких же переливаний получим концентрацию
таких же переливаний получим концентрацию  .
.
Пример 1. (ЕГЭ-2010) Клиент взял в банке кредит 12000 рублей на год под 16 %. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько он должен вносить в банк ежемесячно?
Решение: общая сумма, которую должен выплатить клиент за год, равна  рублей. Поэтому, согласно договору между клиентом и банком, ежемесячная выплата должна быть равна
рублей. Поэтому, согласно договору между клиентом и банком, ежемесячная выплата должна быть равна  рублям. Ответ: 1160 рублей.
рублям. Ответ: 1160 рублей.
Пример 2. Магазин повысил цену на товар вначале на 10%, а затем еще на 20%. На сколько всего процентов выросла цена?
Решение: Пустьпервоначальная цена была равна  . После первого повышения цена станет равной
. После первого повышения цена станет равной 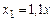 , а после второго -
, а после второго -  . Таким образом, цена повысилась на 32%.
. Таким образом, цена повысилась на 32%.
Ответ: 32%.
Пример 3. Магазин снизил цену на товар вначале на 10%, а затем еще на 20%. На сколько всего процентов оказалась снижена цена?
Решение: Пустьпервоначальная цена была равна  . После первого понижения цена станет равной
. После первого понижения цена станет равной  , а после второго -
, а после второго -  . Таким образом, цена понизилась на 28%.
. Таким образом, цена понизилась на 28%.
Ответ: 28%.
Пример 4. Магазин снизил цену на стиральную машину на 10%, при этом в результате продажи получает прибыль 8%. Какую прибыль получал магазин до снижения цены?
Решение: обозначим за х себестоимость стиральной машины для магазина, то есть цену, по которой магазин приобретал стиральную машину. Пусть в результате продажи стиральной машины магазин получал прибыль  процентов. Это означает, что магазин продавал стиральную машину с наценкой
процентов. Это означает, что магазин продавал стиральную машину с наценкой  процентов, то есть по цене
процентов, то есть по цене 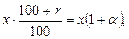
 . После снижения продажной цены на 10% она составила
. После снижения продажной цены на 10% она составила  , и, по условию задачи, равна
, и, по условию задачи, равна  . Из уравнения
. Из уравнения  находим, что
находим, что  = 0,2
= 0,2 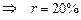 .
.
Ответ: 20%.
Пример 5. Дыня дороже арбуза на 150%. На сколько процентов арбуз дешевле дыни?
Решение: за  следует обозначить цену арбуза. Тогда мы можем найти цену дыни. Она составит
следует обозначить цену арбуза. Тогда мы можем найти цену дыни. Она составит  . Значит, дыня дороже арбуза в 2,5 раза (тогда и арбуз дешевле дыни в 2,5 раза). Теперь нам надо найти, на сколько процентов арбуз дешевле дыни. Для этого разницу в цене (
. Значит, дыня дороже арбуза в 2,5 раза (тогда и арбуз дешевле дыни в 2,5 раза). Теперь нам надо найти, на сколько процентов арбуз дешевле дыни. Для этого разницу в цене (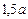 ) нужно поделить на цену дыни. Получим
) нужно поделить на цену дыни. Получим  . Т.о., арбуз дешевле дыни на 60%. Ответ: на 60%.
. Т.о., арбуз дешевле дыни на 60%. Ответ: на 60%.
Пример 6. За некоторый период времени количество акций у гражданина Кириллова увеличилось на 28%. На сколько процентов увеличилась цена каждой акции гражданина Кириллова, если общая стоимость его акций увеличилась на 156%?
Решение: пусть первоначально у гражданина Кириллова было n акций по цене 1 (условная единица) за акцию. Пусть цена каждой акции гражданина Кириллова увеличилась на х %. Тогда общая стоимость акций составила уже  , и, согласно условию задачи, стала составлять 256% от прежней общей стоимости акций. Из уравнения
, и, согласно условию задачи, стала составлять 256% от прежней общей стоимости акций. Из уравнения  находим, что х = 100. Ответ: 100
находим, что х = 100. Ответ: 100
Пример 7. Автомобиль проехал по шоссе, а затем по грунтовой дороге. Путь по шоссе был на 80% больше, чем путь по грунтовой дороге. Время движения по грунтовой дороге было на 20% меньше, чем по шоссе. На сколько процентов средняя скорость движения автомобиля по шоссе больше скорости движения по грунтовой дороге?
Решение: обозначим за S – путь по грунтовой дороге, а за t – время движения по шоссе. Тогда средняя скорость автомобиля по шоссе составила  , а по грунтовой дороге –
, а по грунтовой дороге –  . Поэтому средняя скорость по шоссе составила
. Поэтому средняя скорость по шоссе составила 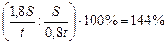 процента от средней скорости по грунтовке. Ответ: на 44%.
процента от средней скорости по грунтовке. Ответ: на 44%.
Пример 8. Хлебопекарня увеличила выпуск продукции на 50%. На сколько процентов изменилась прибыль пекарни и в какую сторону, если отпускная цена её продукции возросла на 10%, а себестоимость продукции, которая до этого составляла 3/4 отпускной цены, увеличилась на 20%?
Решение: Пусть масса продукции первоначально равнялась х кг, а отпускная цена у руб. Используя условие задачи, составим уравнение: Первоначальная прибыль: 
Прибыль после изменений: 


Отношение новой прибыли к старой равно: 
Ответ: прибыль пекарни увеличилась на 20%
Пример 9. Вклад, находящийся в банке с начала года, возрастает к концу года на определённый процент, свой для каждого банка. В начале года Андрей положил 60% некоторой суммы денег в 1-й банк, а оставшуюся часть суммы – во 2-й банк. К концу года сумма этих вкладов стала равна 885000 рублей, а к концу следующего года 1051500 рублей. Если бы Андрей первоначально положил 60% своей суммы во 2-й банк, а оставшуюся часть – в 1-й банк, то по истечении одного года сумма вкладов стала бы равной 915000 рублей. Какова была бы сумма вкладов в этом случае к концу второго года?
Ответ: 
Решение: Пусть S – сумма денег Андрея, 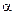 - доля прироста денег в первом банке, а
- доля прироста денег в первом банке, а  - во втором банке. Положим
- во втором банке. Положим 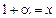 ,
,  .Тогда условия задачи приводят крешению системы уравнений
.Тогда условия задачи приводят крешению системы уравнений
 ,
,
где d нужно найти.
Поделив 3-е уравнение на 1-е, находим, что 

 Поделив 4-е уравнение на 2-е, аналогично находим, что
Поделив 4-е уравнение на 2-е, аналогично находим, что 
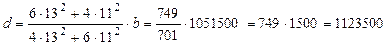 .
.
Пример 10. Алексей приобрёл ценную бумагу за 7000 рублей. Цена бумаги каждый год возрастает на 2000 рублей. В любой момент Алексей может продать бумагу и положить деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение какого года Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте оказалась наибольшей?
Ответ: в течение восьмого года
Решение: Пока бумага лежит дома ее стоимость растет в арифметической прогрессии с разностью 2000, а в банке она будет расти в геометрической прогрессии со знаменателем 1,1. Алексей должен продать ценную бумагу, когда лишний год держать ее дома становится невыгодно. Пусть Алексей держит бумагу дома n лет, а на оставшиеся 30- n лет кладет их в банк. Тогда через 30 лет у него будет сумма  . Нужно найти такое n, чтобы если держать ценную бумагу дома (n +1) год, то сумма через 30 лет будет меньше. Т.о., исходная задача сводится к решению неравенства в натуральных числах.
. Нужно найти такое n, чтобы если держать ценную бумагу дома (n +1) год, то сумма через 30 лет будет меньше. Т.о., исходная задача сводится к решению неравенства в натуральных числах. 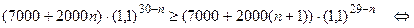
 .
.
Следовательно, дома нужно держать бумагу 7 лет, а продать и положить деньги в банк нужно в течение восьмого года.
Более подробно с авторскими решениями заданий 19 этого и других типов можно ознакомиться по ссылке https://goo.gl/ttk8ag.
Кредиты.
Рассмотрим общую ситуацию.
Пусть S – сумма, взятая клиентом в кредит на n лет (или месяцев) под r % в год (или в месяц). В долях это будет – под долю  , причем процент начисляется на оставшуюся сумму долга.
, причем процент начисляется на оставшуюся сумму долга.
Пусть 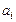 - выплата долга в
- выплата долга в  -ый год (или месяц), а
-ый год (или месяц), а  - суммарные выплаты по кредиту.
- суммарные выплаты по кредиту.
Обозначим через  - оставшийся долг после
- оставшийся долг после  -ой выплаты. Тогда
-ой выплаты. Тогда




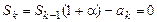
……………………
 .
.
Сложив все уравнения, получим
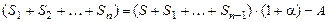 .
.
Добавив к обеим частям S и учитывая, что 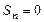 , получим
, получим
 , отсюда можно найти переплату
, отсюда можно найти переплату
 .
.
1). В конкретной задаче последовательность  может образовывать убывающую арифметическую прогрессию с разностью d, т.е.
может образовывать убывающую арифметическую прогрессию с разностью d, т.е. 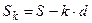 , тогда и последовательность выплат
, тогда и последовательность выплат  образует убывающую арифметическую прогрессию. Найдем разность и этой арифметической прогрессии. Из равенства
образует убывающую арифметическую прогрессию. Найдем разность и этой арифметической прогрессии. Из равенства  найдем
найдем  .
.
Тогда 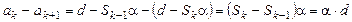
или 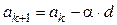 , т.е. все выплаты тоже образует убывающую арифметическую прогрессию с разностью
, т.е. все выплаты тоже образует убывающую арифметическую прогрессию с разностью 
Тогда
 , откуда формула переплаты примет вид:
, откуда формула переплаты примет вид:  ,
,
а из равенства  получим
получим  .
.
Можно найти и сумму выплат за k лет (или месяцев):

Пример 11. 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Какую сумму следует взять в кредит, чтобы общая сумма выплат после полного его погашения равнялась 1 млн. рублей?
Решение. Пусть S – сумма, взятая клиентом в кредит на 24 месяца под 2% в месяц. По условию задачи  .
.
Применяя формулу переплаты 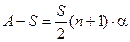 , где А=1 млн., получим
, где А=1 млн., получим  .
.
Ответ: 800000 рублей.
В 2018 году условие задачи немного изменили и резко снизилась доля решивших задачу.
Пример 12. 15-го января планируется взять кредит в банке сумме S тыс.рублей на n месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца в течение первых (n -1) месяцев.
Какую сумму составит последний платеж, чтобы общая сумма выплат после полного его погашения равнялась А тыс. рублей?
(Цифры А, S, r и n были известны).
Решение. Пусть S – сумма, взятая клиентом в кредит на n месяцев под r % в месяц.
Применяя формулу переплаты  и учитывая, что
и учитывая, что  , а
, а  образуют убывающую арифметическую прогрессию, получим
образуют убывающую арифметическую прогрессию, получим  .
.
Из этого равенства найдем 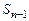
 .
.
Из последнего равенства 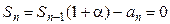 найдем
найдем  . Получим
. Получим  .
.
Из 5 неизвестных в последнем равенстве могли быть известны любые 4, пятая находится из этого равенства.
Пример 13. Клиент банкавзял в кредит 360 тысяч рублей на 36 месяцев под 4% в месяц на условиях равномерного помесячного уменьшения долга. На сколько тысяч рублей меньше переплатил бы в сумме клиент, если бы он взял кредит на 24 месяца под те же 4% в месяц на условиях равномерного помесячного уменьшения долга?
Ответ: на 86,4 тыс. руб.
Решение. Пусть S=360 тыс. руб. – сумма, взятая клиентом в кредит на 36 месяцев под 4% в месяц. По условию задачи  .
.
Применяя формулу переплаты 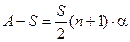 , где S=360, n =36, получим
, где S=360, n =36, получим 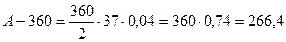
Пусть S=360 тыс. руб. – сумма, взятая клиентом в кредит на 24 месяца под 4% в месяц. По условию задачи  .
.
Применяя формулу переплаты 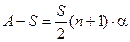 , где S=360, n =24, получим
, где S=360, n =24, получим  . Т.о., во втором случае клиент переплатил бы меньше на 86,4 тыс. руб.
. Т.о., во втором случае клиент переплатил бы меньше на 86,4 тыс. руб.
Пример 14. Клиент взял кредит в банке на три года под 20% годовых, начисляемых в конце каждого года на текущую сумму долга. Ежегодные выплаты производятся в начале следующего года и образуют убывающую арифметическую прогрессию. Найдите величину первого платежа, если взятая в кредит сумма равна 510000 рублей, а общая сумма выплат по кредиту составила 714000 рублей. Ответ: 272 000 рублей
Решение. Пусть S=510 тыс. руб. – сумма, взятая клиентом в кредит на 3 года под 20% в месяц. По условию задачи  ,
,
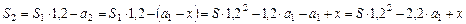
 .
.
Общая сумма выплат равна 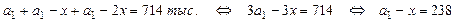 .
.
Получили систему: 

Пример 15. В июле планируется взять кредит в банке на сумму 4,5 млн рублей на срок 9 лет. Условия его возврата таковы:
— каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший — не менее 0,6 млн рублей. Ответ: 20%
Решение. Пусть S = 4,5 млн. руб. – сумма, взятая клиентом в кредит на 9 лет под r % годовых ( ). Поскольку долг после начисления процентов и очередной выплаты образует убывающую арифметическую прогрессию с разностью
). Поскольку долг после начисления процентов и очередной выплаты образует убывающую арифметическую прогрессию с разностью  , то и выплаты образуют убывающую арифметическую прогрессию с разностью
, то и выплаты образуют убывающую арифметическую прогрессию с разностью 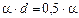 . Поэтому наибольший платеж – первый, а наименьший – последний. При этом,
. Поэтому наибольший платеж – первый, а наименьший – последний. При этом,  . Тогда
. Тогда  . Получаем систему неравенств:
. Получаем систему неравенств:
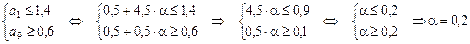
Т.о.,  .
.
2). В конкретной задаче также могут быть равные выплаты по кредиту. В этом случае для последовательности долгов  можно получить формулу. Обозначим
можно получить формулу. Обозначим  .
.
 ;
;  ;
;
 и т.д.
и т.д.
 .
. 
Пример 16. В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r. Ответ: 10%.
Решение. Пусть S – сумма, взятая клиентом в кредит на n лет под r % годовых ( ). Если в первом случае ежегодные равные выплаты равны
). Если в первом случае ежегодные равные выплаты равны  , то
, то 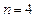 , а если они равны
, а если они равны  , то
, то  . По формуле
. По формуле 
 . Отсюда
. Отсюда
 .
.
Поделив первое уравнение на второе, получим 
 Отсюда
Отсюда 
Пример 17. Клиент банкавзял в кредит 400 тысяч рублей на три года под 20% годовых на условиях помесячной выплаты равными долями. Через год клиент договорился с банком о досрочном (за два года вместо трёх лет) погашении кредита. На сколько тысяч рублей больше будет выплачивать ежемесячно клиент во второй год, чем в первый?
Ответ: на 9,6 тыс. руб.
Решение. Пусть S = 400 тыс. руб. – сумма, взятая клиентом в кредит на 3 года под 20% годовых ( ). Ежемесячная выплата в первый год составит
). Ежемесячная выплата в первый год составит  . За 12 месяцев он выплатит сумму, равную
. За 12 месяцев он выплатит сумму, равную  . По новому договору через 2 года его долг будет равен
. По новому договору через 2 года его долг будет равен 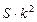 , а значит ему останется выплатить сумму
, а значит ему останется выплатить сумму  . И каждый месяц придется выплачивать
. И каждый месяц придется выплачивать  . Разница составит 9,6 тыс. руб.
. Разница составит 9,6 тыс. руб.
Пример 18. В середине января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения:
| Дата | 15.01 | 15.02 | 15.03 | 15.04 | 15.05 | 15.06 | 15.07 |
| Долг (в процентах от кредита) | 100% | 90% | 80% | 70% | 60% | 50% | 0% |
В конце каждого месяца, начиная с января, текущий долг увеличивается на 5%, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат больше суммы самого кредита? Ответ: на 22,5%
Решение. Пусть S – сумма, взятая клиентом в кредит на 6 месяцев под 5% годовых (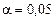 ). Тогда
). Тогда
 ;
;
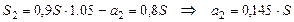 ;
;
 ;
;
 ;
;
 ;
;
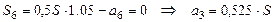 .
.
Найдем общую сумму выплат:  . Она превышает сумму кредита на
. Она превышает сумму кредита на  , т.е. на 22,5%.
, т.е. на 22,5%.
3) Совершенно аналогично выглядит модель решения задач, когда клиент кладет деньги в банк под долю 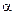 , и каждый год (или месяц) добавляет (или снимает) некоторую сумму денег.
, и каждый год (или месяц) добавляет (или снимает) некоторую сумму денег.
Пример 19. Клиент хочет положить деньги в банк под 15% годовых так, чтобы в конце первого года (после начисления процентов) снять 120 тысяч рублей, в конце второго года (после начисления процентов на оставшуюся сумму) снова снять 120 тысяч рублей, а в конце третьего года (после начисления процентов на оставшуюся сумму) снять не менее миллиона рублей. Какое минимальное целое число тысяч рублей должен положить в банк клиент, чтобы указанные условия могли быть выполнены?
Ответ: 
Решение. Пусть S – сумма, которую клиент хочет положить в банк 15% годовых ( ). Тогда
). Тогда
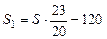 ;
;
 ;
;
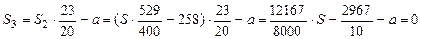 .
.
Отсюда 
 . Следовательно, наименьшее целое S = 853 тысячи.
. Следовательно, наименьшее целое S = 853 тысячи.
Пример 20. Клиент взял кредит в банке на три года под 20% годовых, начисляемых в конце каждого года на текущую сумму долга. Ежегодные выплаты производятся в начале следующего года и образуют возрастающую арифметическую прогрессию. Найдите величину последнего платежа, если взятая в кредит сумма равна 300000 рублей, а общая сумма выплат по кредиту составила 436500 рублей.
Ответ: 171000.
Решение: Пусть а - величина первого платежа, а d – разность прогрессии, тогда величина последнего платежа а + 2 d находится из уравнений  и
и 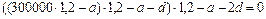 , решая которые найдем a и d, а затем и а + 2 d.
, решая которые найдем a и d, а затем и а + 2 d.
Задачи на смеси и сплавы
| Основной принцип при решении задач на смеси и сплавы, на растворы и т.п.: «Приравниваем чистое вещество» |
Пример 21. Свежие грибы содержат 90% воды, а сухие - 12% воды. Сколько получится сухих грибов из 22 кг свежих грибов?
Решение: в 22 кг свежих грибов содержится 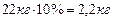 «абсолютно сухого грибного вещества». Пусть
«абсолютно сухого грибного вещества». Пусть 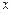 кг - масса сухих грибов. В сухих грибах эти 2,2 кг составляют 88% веса. Приравнивая сухое вещество, получим
кг - масса сухих грибов. В сухих грибах эти 2,2 кг составляют 88% веса. Приравнивая сухое вещество, получим 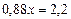 . Поэтому вес сухих грибов будет равен
. Поэтому вес сухих грибов будет равен  . Ответ: 2,5 кг
. Ответ: 2,5 кг
Пример 22. Имеются три сплава. Первый сплав содержит 70% олова и 30% свинца, второй – 80% олова и 20% цинка, третий – 50% олова, 10% свинца и 40% цинка. Из них необходимо приготовить новый сплав, содержащий 15% свинца. Какое наименьшее и какое наибольшее процентное содержание олова может быть в этом новом сплаве?
Решение: обозначим за 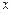 – массу нового сплава, за
– массу нового сплава, за 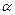 - долю олова в новом сплаве, за а – массу, взятую от первого сплава, за b – массу, взятую от второго сплава. Условия задачи запишем в виде следующей таблицы:
- долю олова в новом сплаве, за а – массу, взятую от первого сплава, за b – массу, взятую от второго сплава. Условия задачи запишем в виде следующей таблицы:
| олово | свинец | цинк | масса | |
| 1-й сплав | 0,7 
| 0,3 
| - | a |
| 2-й сплав | 0,8 
| - | 0,2 
| b |
| 3-й сплав | 0,5(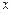 - -  - -  ) )
| 0,1(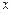 - -  - -  ) )
| 0,4( - -  - -  ) )
|  – a – b – a – b
|
| новый сплав | 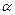 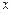
| 0,15 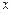
| (0,85 – 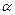 ) x ) x
| 
|
Приравниваем массу свинца из всех кусков к массе свинца в новом сплаве:  .Отсюда находим
.Отсюда находим 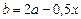 .
.
Из условия приравниваем массу олова из всех кусков к массе олова в новом сплаве: 
Раскрывая скобки, получим уравнение 
Отсюда находим, что  . Полагая
. Полагая  , получим:
, получим:  . Таким образом, процент
. Таким образом, процент 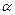 олова в новом сплаве является линейной возрастающей функцией от k. Область возможных значений k определится системой условий
олова в новом сплаве является линейной возрастающей функцией от k. Область возможных значений k определится системой условий  , откуда
, откуда  . Тогда
. Тогда  , а
, а  . Ответ: 55% и 75%
. Ответ: 55% и 75%
Пример 23. (экономический факультет МГУ) Банк планирует вложить на один год 40% имеющихся у него средств клиентов в проект Х а остальные 60% – в проект Y. В зависимости от обстоятельств проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y – прибыль в размере от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определите наименьший и наибольший возможный уровень процентной ставки по вкладам, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.
Решение: минимальный планируемый годовой доход банка равен  . Поэтому наименьший возможный уровень процентной ставки по вкладам будет равен 25% – 15% = 10%. Аналогично, максимальный планируемый годовой доход банка равен
. Поэтому наименьший возможный уровень процентной ставки по вкладам будет равен 25% – 15% = 10%. Аналогично, максимальный планируемый годовой доход банка равен  . Поэтому наименьший возможный уровень процентной ставки по вкладам будет равен 30% – 10% = 20%.
. Поэтому наименьший возможный уровень процентной ставки по вкладам будет равен 30% – 10% = 20%.
Ответ: 10% и 20%.
Пример 24. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5% в месяц, затем  потом
потом 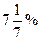 и, наконец, 12% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на 180%. Определить срок хранения вклада.
и, наконец, 12% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на 180%. Определить срок хранения вклада.
Решение: пусть x – исходная сумма. Ежемесячные проценты в долях составляют 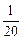 ,
,  ,
,  и
и  . Пусть n месяцев начислялась доля
. Пусть n месяцев начислялась доля 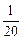 ,
,
m месяцев – доля  , k месяцев – доля
, k месяцев – доля  и p месяцев – доля
и p месяцев – доля  . Тогда по истечении n+m+k+p месяцев сумма вклада станет равной
. Тогда по истечении n+m+k+p месяцев сумма вклада станет равной  . Получим уравнение:
. Получим уравнение:  или
или  . Разложив все числа на простые множители, получим:
. Разложив все числа на простые множители, получим:  или
или 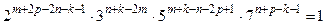 . Равенство возможно только в том случае, когда все показатели степеней равны нулю, т.е.
. Равенство возможно только в том случае, когда все показатели степеней равны нулю, т.е.
 . Сложив первые 3 уравнения, а затем третье и четвертое, получим
. Сложив первые 3 уравнения, а затем третье и четвертое, получим 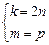 . Подставляя эти выражения в первые три уравнения, дополнительно получим
. Подставляя эти выражения в первые три уравнения, дополнительно получим  . Отсюда следует, что
. Отсюда следует, что  . Таким образом, срок хранения вклада составил n+m+k+p = 12 месяцев.
. Таким образом, срок хранения вклада составил n+m+k+p = 12 месяцев.
Ответ: 12 месяцев.