При решении этой задачи мы использовали неравенство Коши

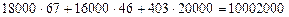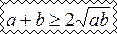
между средним арифметическим и средним геометрическим двух положительных чисел a и b. Отметим, что равенство достигается тогда и только тогда, когда a = b.

Если оба слагаемых положительны, то Причем минимальное значение выражения достигается, когда

В нашем примере:

Пример 39. Точки 1 и 2 движутся по осям 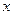и 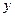к началу координат. В момент 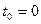точка 1 находится на расстоянии 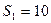см, а точка 2 – на расстоянии 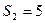см от начала координат. Первая точка движется со скоростью 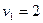см/с, а вторая – со скоростью 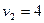см/с. Каково наименьшее расстояние между ними?

Решение. В момент расстояние (в см.) между точками равно

(рис. 1):

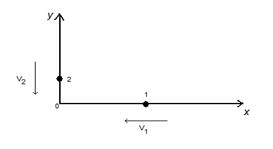
рис. 1

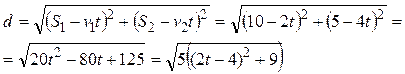
Минимум выражения, стоящего под знаком радикала, как и самого расстояния 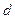будет достигаться при , откуда (см). Ответ: см.

Пример 40. (МГУ, 1996) (Задачи такого типа встречаются в заданиях ЕГЭ под № 17) В контейнер упакованы изделия двух типов. Стоимость и вес одного изделия составляют 400 тыс. руб. и 12 кг для первого типа и 600 тыс. руб. и 15 кг для второго типа. Общий вес изделий равен 321 кг. Определите минимальную и максимальную возможную суммарную стоимость находящихся на контейнере изделий.

Решение. Пусть 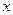и 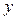- число изделий первого и второго типа соответственно. Тогда общий вес изделий равен , а их суммарная стоимость равна .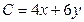

Теперь переформулируем задачу: найти наименьшее и наибольшее значения функции при условии, что 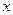и 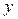- натуральные числа, удовлетворяющие соотношению .

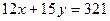Решим это уравнение: ,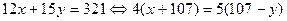

где 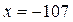, частное решение уравнения.

Так как числа 4 и 5 – взаимно простые, общее решение этого уравнения в целых числах имеет вид: , .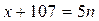

Общее решение уравнения в целых числах имеет вид:

, .

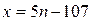Нас интересует решение в натуральных числах. Это означает, что 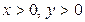, т.е.

Отсюда . Итак, натуральным решениям соответствуют значения параметра .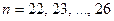

Используя полученные результаты, мы можем переформулировать исходную задачу следующим образом: найти наименьшее и наибольшее значения функции 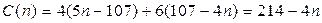при условии, что параметр .

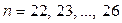Поскольку зависимость - линейная с отрицательным коэффициентом, наименьшее значение достигается при 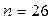, а наибольшее – при .

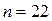Ответ. 11 000 тыс. руб. и 12 600 тыс. руб.

Разные задачи

Пример 41. (ЕГЭ-2010) Зависимость температуры (в градусах Кельвина) от времени (в минутах) для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур задаётся выражением , где , , 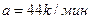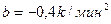. Известно, что при температурах нагревателя свыше 1000 k прибор может испортиться, поэтому его нужно отключать. Определите (в минутах) через какое наибольшее время после начала работы нужно отключать прибор.

Решение: задача сводится к решению неравенства , или .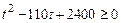

Множество решений этого неравенства имеет вид .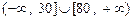

С учётом здравого смысла заключаем, что наибольшее время работы прибора составляет 30 минут. Ответ: 30 минут.

Пример 42. (экономический факультет МГУ) В первый день у Васи было на 30 рублей больше, чем у Пети. Вася внес на покупку книг 1/n часть своих денег, Петя - ½ часть своих денег, при этом Петя внёс на 20 руб. больше Васи. На второй день мальчики пошли за тетрадями. На этот раз у Васи было на 60 рублей больше, чем у Пети. На покупку тетрадей Вася снова внёс 1/n часть своих денег, а Петя - ¼ часть своих. При этом Вася внёс на 40 рублей больше. Найти количество денег у Васи и у Пети в 1-ый день, если известно, что все суммы целочисленные.

Решение: пусть m – количество рублей у Васи в первый день, а k – количество рублей у Пети во второй день. Тогда получаем следующую систему уравнений 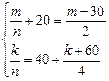, в которой все слагаемые являются целыми числами. Обозначив натуральные числа 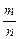и как p и q соответственно, перепишем эту систему в виде , откуда . Так как n, p и q – натуральные числа, то возможен только случай n = 3, так что p = 70 и q = 220. Тогда m = 210 рублей было у Васи в первый день, и m – 30 = 180 рублей было у Пети в первый день.

Ответ: 210 и 180.

Пример 43. В шахматном турнире участвовало более 9, но менее 25 шахматистов – гроссмейстеров и мастеров. По окончании турнира выяснилось, что каждый участник набрал против гроссмейстеров половину своих очков. Сколько человек участвовало в турнире? Сколько среди них было мастеров?

Решение: пусть в турнире участвовали m гроссмейстеров и n мастеров. Тогда гроссмейстеры во встречах между собой набрали 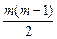очков, мастера во встречах между собой набрали 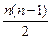очков, а во встречах между гроссмейстерами и мастерами было набрано очков. Из условий задачи получаем последовательно: 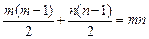, , 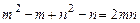. Отсюда заключаем, что или 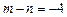. Так как гроссмейстеры в целом играют сильнее мастеров, то во встречах между гроссмейстерами и мастерами большую часть из всех набранных очков набрали гроссмейстеры. А тогда и , так что . Поэтому возможен только случай . 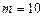А так как , то и .

Ответ: 16 и 6.

Пример 44. Для того, чтобы купить в харчевне полпорции жареных пескарей, коту Базилио не хватает 3 сольдо, а лисе Алисе – 10 сольдо. Они закопали свои деньги на поле Чудес, и на следующий день их совместный капитал утроился. Смогут ли теперь кот Базилио и лиса Алиса купить порцию жареных пескарей на двоих?

Решение: пусть х сольдо стоят полпорции жареных пескарей. Тогда у кота имеется (х – 3) сольдо, а у лисы – (х – 10) сольдо, так что х >10. После того, как совместный капитал утроился, у кота и лисы на двоих стало сольдо. Это больше, чем 2 х – стоимость порции жареных пескарей, так как .

Ответ: да, смогут.

Пример 45. Гриб называется «плохим», если в нём больше 11 червяков. Червяк называется «тощим», если он съел не более 1/5 гриба, в котором живёт. Четверть всех грибов в лесу – «плохие». Докажите, что не менее трети всех червяков в лесу – «тощие».

Доказательство: обозначим за n число «плохих» грибов. Тогда 3 n – число «хороших» грибов. В каждом «плохом» грибе не менее 12 червяков, причём из них не более 4 «толстых», и, значит, не менее 8 «тощих». В каждом «хорошем» грибе не более 11 червяков, причём из них тоже не более 4 «толстых». Поэтому в лесу не менее 8 n «тощих» червяков и не более 16 n «толстых» червяков. Поэтому не менее трети всех червяков в лесу – «тощие».

Пример 46. (НГУ) В пяти диктантах школьник ошибся 31 раз, причем в каждом следующем диктанте он делал ошибок меньше, чем в предыдущем. В последнем диктанте школьник ошибся в три раза меньше, чем в первом. Сколько ошибок допустил школьник во втором диктанте?

Решение: пусть n – количество ошибок в пятом диктанте, тогда3 n – количество ошибок в первом диктанте. Пусть m, k и l – количество ошибок соответственно во втором, в третьем и в четвёртом диктантах. Тогда 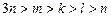и 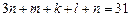. Так как , то 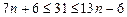. Последнее двойное неравенство может выполняться только при 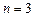. Отсюда получаем, что 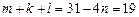. Так как 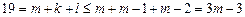, а, с другой стороны, , то 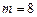. Ответ: 8.

Пример 47. (мех-мат НГУ) Предприниматель купил акции компании First по цене 12 у.е. за акцию и компании Sekond по 9 у.е. за акцию, причём количество акций первой компании более чем на 5 превосходило количество акций второй компании, а общая стоимость была менее 390 у.е. Через некоторое время стоимость акции компании First возросла до 18 у.е за, а акции компании Sekond – до 21 у.е., и предприниматель продал акции более чем за 692 у.е. Определите количество акций каждой компании.

Решение: пусть m – количество акций первой компании, а n – количество акций второй компании. Тогда условия задачи приводят к следующей системе неравенств в натуральных числах:

.

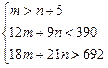Решая каждое из неравенств относительно n, получаем: .

Составляя из полученных относительно m неравенств все возможные цепочки неравенств и опуская m, получим систему

, то есть .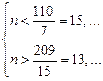

Поэтому n равно 14 или 15. Если n равно 14, то для нахождения получаем следующую систему неравенств в натуральных числах: 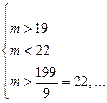. Эта система не имеет решений. Если же n равно 15, то для нахождения получаем следующую систему неравенств в натуральных числах: . Эта система имеет единственное решение m = 21.

Ответ: 21 акция First и 15 акций Sekond.

Пример 48. (C6 ЕГЭ) Про натуральные числа a, b, c известно, что числа 3 a + 2 b + c и 2 a + b + 2 c оканчиваются в

десятичной записи на цифру 0. На какую цифру может оканчиваться

число c, если число b оканчивается на цифру 2?

Решение: так как числа 3 a + 2 b + c и 2 a + b + 2 c оканчиваются на цифру 0, то и число также оканчивается на цифру 0. А так как число b оканчивается на цифру 2, то и число 4 с также оканчивается на цифру 2. Поэтому число с может оканчиваться только на 3 или на 8. Ответ: на 3 или на 8.

Пример 49. Цена одной продаваемой автомашины – 20000 у.е. Из 516 машин каждая 7-ая продаётся со скидкой 10%, а каждая 11-ая – 20%. Если на машину распространяются обе скидки, то берётся бóльшая. Найти выручку с продажи.

Ответ: 10002000.

Решение: Пусть k машин продается со скидкой 10%, т.е. по 18000 руб. Т.к. 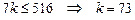. Пусть n машин продается со скидкой 20%, т.е. по 16000 руб. Т.к. . Количество машин с двумя скидками находим из неравенства 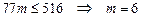. Итак, продали 67 машин по 18000 руб., 46 машин по 16000 руб., 46 и оставшиеся 403 машины по 20000 руб.

Поэтому выручка составила