ЛЕКЦИЯ 8. Нормализация БД. Часть1
Понятие функциональной зависимости[2]
Создание баз данных преследует две основные цели [4, 14, 24]:
§ понизить избыточность хранимых данных;
§ повысить их надежность.
Любое априорное знание о различные рода ограничениях, накладываемых на совокупности данных, может принести большую пользу для достижения указанных целей.
Один из способов формализации этих знаний – установление зависимостей между элементами данных. Известно два основных типа таких зависимостей:
1) функциональные зависимости;
2) многозначные зависимости.
Функциональная зависимость является обобщением понятия ключа.
В табл. 8.1 представлено отношение
График (ПИЛОТ, РЕЙС, ДАТА, ВРЕМЯ-ВЫЛЕТА).
Это отношение показывает, какой пилот участвует в данном рейсе в данный день и каково время вылета самолета. Не любое сочетание значений атрибутов ПИЛОТ, РЕЙС, ДАТА и ВРЕМЯ-ВЫЛЕТА допустимо в таком расписании. На табл. 8.1 накладываются следующие ограничения.
1. Для каждого рейса назначается только одно время вылета.
2. Для данного пилота, даты и времени вылета возможен только один рейс.
3. Для данного рейса и даты назначается только один пилот.
Эти ограничения являются примерами F-зависимостей (F-зависимость – функциональная зависимость между данными).
F-зависимость имеет место тогда, когда значения кортежа на одном множестве атрибутов единственным образом определяют эти значения на другом множестве атрибутов.
Таблица 8.1
| График | ПИЛОТ | РЕЙС | ДАТА | ВРЕМЯ-ВЫЛЕТА |
| Мовчан | 9 августа | 10:15 | ||
| Мовчан | 10 августа | 13:25 | ||
| Синицын | 8 августа | 05:50 | ||
| Синицын | 12 августа | 18:35 | ||
| Синицын | 11 августа | 10:15 | ||
| Федотов | 13 августа | 10:15 | ||
| Федотов | 12 августа | 13:25 | ||
| Вишневский | 9 августа | 05:50 | ||
| Вишневский | 13 августа | 05:50 | ||
| Вишневский | 15 августа | 13:25 |
Указанные выше ограничения можно сформулировать следующим образом.
1. ВРЕМЯ функционально зависит от РЕЙСА.
2. РЕЙС функционально зависит от {ПИЛОТ, ДАТА, ВРЕМЯ}.
3. ПИЛОТ функционально зависит от {РЕЙС, ДАТА}.
Порядок в этих последовательностях могут менять и говорить, что РЕЙС, ДАТА функционально определяют ПИЛОТ, или символически:
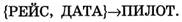
Пусть r – отношение со схемой R, X и Y – подмножества R. Отношение r удовлетворяет функциональной зависимости X → Y, если
 (8.1)
(8.1)
В F-зависимости Х → Y подмножество X называется левой частью, а Y – правой частью.
Аксиомы вывода функциональных зависимостей
Для отношения r(R) в любой момент существует некоторое семейство F-зависимостей, которым это отношение удовлетворяет. Здесь может возникнуть та же проблема, что и с ключами: одно состояние отношения может удовлетворять F-зависимости, а другое – нет.
Требуется выявить семейство F-зависимостей F, которому удовлетворяют все допустимые состояния r. Чтобы найти F, необходимы семантические знания об отношении r. Поэтому можно считать семейство F-зависимостей заданным в схеме отношения R, в этом случае любое отношение r (F) должно удовлетворять всем F-зависимостям из F. Не всегда ясно, что является первичным: множество допустимых состояний отношения, которое определяет F-зависимости, или F-зависимости накладывают ограничения на схему отношения [14].
Множество функциональных зависимостей, применимых к отношению r(R), конечно, так как существует только конечное число подмножеств множества R. Таким образом, всегда можно найти все F-зависимости, которым удовлетворяет r. Однако этот подход требует большого количества шагов и, соответственно, много времени.
Если известны некоторые F-зависимости из F, то часто можно вывести остальные.
Множество F-зависимостей F влечет за собой зависимость X → Y, если каждое отношение, удовлетворяющее всем зависимостям в F, удовлетворяет также зависимости X → Y.
Аксиома вывода - это правило, устанавливающее, что если отношение удовлетворяет определенным F-зависимостям, то оно должно удовлетворять и некоторым другим F-зависимостям.
Сформулировано шесть аксиом вывода F-зависимостей [14]. В этих формулировках используется обозначение r для отношения на R и W, X, Y и Z – для подмножеств R.
F1. Рефлексивность. Х → Х.
F2. Пополнение. Х → Y влечет за собой XZ → Y.
F3. Аддитивность. X → У и X → Z влечет за собой X → YZ.
F4. Проективность. X → YZ влечет за собой X → Y.
F5. Транзитивность. Х → Y и Y → Z влечет за собой X → Z.
F6. Псевдотранзитивность. X → Y и YZ → W влечет за собой XZ → W.
Некоторые аксиомы вывода могут быть получены из других. Например, транзитивность F5 является частным случаем псевдотранзитивности F6 при Z = Æ.
Приведенная система аксиом F1-F6 является полной. Это означает, что каждая F-зависимость, которая следует из множества F, может быть выведена путем одно- или многократного применения к F этих аксиом.
Из аксиом F1, F2 и F6 можно вывести остальные, а значит, они образуют полное подмножество для F1-F6. Аксиомы F1, F2 и F6 являются также независимыми: ни одна из этих аксиом не может быть получена из двух других. Иногда эти три аксиомы называются аксиомами Армстронга.
Пусть F – множество F-зависимостей для отношения r(R). Замыкание F, обозначаемое F+, – это наименьшее содержащее F множество, такое, что при применении к нему аксиом Армстронга нельзя получить ни одной F-зависимости, не принадлежащей F. Так как F+ должно быть конечно, то можно вычислить его, начиная с F путем применения F1, F2 и F6 и добавления полученных F-зависимостей к F до тех пор, пока не перестанут получаться новые зависимости. Замыкание F зависит от схемы R.
Из множества F можно вывести F-зависимость X → Y, если X → Y принадлежит F+. Так как аксиомы вывода порождают только функциональные зависимости, то F влечет за собой X → Y, если X → Y выводится из F.
Пример 1. Пусть F = {AB → C, С → В} - множество F-зависимостей на r (АВС).
Тогда:

В свете новых знаний об F-зависимостях, следует уточнить понятия ключа и суперключа.
Для данной схемы отношения R ключ - это подмножество К Í R, такое, что для любого допустимого отношения r(R) не существует двух различных кортежей t 1 и t 2 в r, таких, что r 1 К) = t 2 (К), и никакое собственное подмножество K' Ì K не обладает этим свойством.
Для некоторых допустимых отношений со схемой R подмножество К' может быть ключом, но рассматриваются все допустимые отношения со схемой R.
Суперключ – это любая совокупность атрибутов, содержащая ключ.
Нормализация - формальный метод анализа отношений на основе их первичного ключа (или потенциальных ключей) и существующих функциональных зависимостей [4, 10, 14].
Цель нормализации – получение такого проекта базы данных, в котором каждый факт хранится в одном месте, т.е. исключена избыточность информации. Это делается не столько с целью экономии памяти, сколько для исключения возможной противоречивости хранимых данных из-за их избыточности. Нормальная форма представляет собой ограничение на схему базы данных (отношения), которое избавляет базу данных от некоторых нежелательных свойств.
Нормализация чаще всего выполняется в несколько последовательных этапов, результатом каждого из которых является некоторая нормальная форма с известными свойствами. В теории реляционных баз данных разработано несколько нормальных форм (НФ), которые подчиняются правилу вложенности (рис. 8.1).

Рис. 8.1. Вложенность нормальных форм
Смысл вложенности нормальных форм в следующем: каждая нормальная форма является в некотором смысле более ограниченной, но и более желательной, чем предшествующая [24]. Это связано с тем, что (N + 1)-я нормальная форма не обладает некоторыми недостатками, свойственным N -йнормальной форме. Общий смысл дополнительного условия, налагаемого на (N + 1)- ю нормальную форму по отношению к N- йнормальной форме, состоит в исключении этих недостатков.
При реализации реляционной БД важно понимать, что только удовлетворение требований первой нормальной формы (1НФ) обязательно для создания отношений приемлемого качества. Все остальные формы могут использоваться по желанию проектировщика. Однако чтобы избежать аномалий обновления, описываемых ниже, нормализацию рекомендуется проводить как минимум до ЗНФ.
Первая нормальная форма
Схема отношения R находится в первой нормальной форме (1НФ), если значения в домене D(A) являются атомарными для каждого атрибута А в JR. Другими словами, значения в домене не являются ни списками, ни множествами простых или сложных значений [14].
Схема базы данных R находится в первой нормальной форме, если каждая схема отношения в R находится в 1НФ.
Определить понятие атомарности трудно: значение атомарное в одном приложении, может быть неатомарным в другом. Можно руководствоваться общим принципом, что значение неатомарною, если в приложении оно используется по частям.
Пример 2. Имеется отношение Сотрудники:
| Сотрудники | НОМЕР | ФИО |
| Вербов Александр Владимирович | ||
| Фисенко Александр Сергеевич | ||
| Фатхи Дмитрий Владимирович |
Если понадобится указать только фамилии сотрудников, то указанное отношение не находится в 1НФ, так как требуемые значения являются частью атрибута ФИО. Чтобы отношение в таких условиях находилось в 1НФ, атрибут ФИО должен быть разбит на части, как показано ниже.
| Сотрудники | НОМЕР | ФАМИЛИЯ | ИМЯ | ОТЧЕСТВО |
| Вербов | Александр | Владимирович | ||
| Фисенко | Александр | Сергеевич | ||
| Фатхи | Дмитрий | Владимирович |
Пример 3. Отношение Род, представленное ниже, не находится в первой нормальной форме потому, что оно включает величины, являющиеся совокупностью атомарных значений.
| Род | ИМЯ | ПОЛ |
| Иван, Александр, Сергей | мужской | |
| Мария, Ирина | женский |
Чтобы отношение Род находилось в 1НФ, оно должно быть представлено следующим образом.
| Род | ИМЯ | ПОЛ |
| Иван | мужской | |
| Александр | мужской | |
| Сергей | мужской | |
| Мария | женский | |
| Ирина | женский |
В чем преимущество применения 1НФ? В том, что 1НФ позволяет выражать F-зависимости с той степенью детализации, с какой требует приложение, что невозможно без 1НФ.
Но и 1НФ обладает рядом существенных недостатков [4, 10, 14]. На первых этапах проектирования базы данных, после анализа предметной области и определения состава информации для хранения в БД обычно формируется так называемое универсальное отношение.
Универсальное отношение – одна таблица, находящаяся в 1НФ, в которой может храниться вся информация об интересующей предметной области. Другими словами схему этого отношения образует весь перечень интересующих атрибутов предметной области [8].
При использовании универсального отношения возникают следующие проблемы [8, 14].
1. Избыточность. Данные многих столбцов многократно повторяются. Повторяются и некоторые наборы данных.
2. Аномалии обновления:
а) аномалии добавления;
б) аномалии изменения;
в) аномалии удаления.
Аномалии обновления являются нежелательным побочным эффектом, обусловленным избыточностью хранимых данных при внесении изменений в отношение.
Рассмотрим отношение График.
| График | РЕЙС | ДАТА | ПИЛОТ | ГАЛЕРЕЯ |
| 6 июня | Иванов | |||
| 7 июня | Петров | |||
| 9 июня | Иванов |
Атрибуты РЕЙС ДАТА являются ключом отношения График, и это отношение должно также удовлетворять F-зависимости РЕЙС→ГАЛЕРЕЯ. Пусть требуется обновить отношение, указав значение ключа и задавая значения всем остальным атрибутам. Однако если выполнить операцию
ИЗМЕНИТЬ (График; 112, 6 июня, ПИЛОТ=Иванов, ГАЛЕРЕЯ=8),
то отношение перестанет удовлетворять F-зависимости РЕЙС→ГАЛЕРЕЯ. Чтобы избежать нарушения F-зависимости, необходимо после каждого выполнения операции обновления просмотреть полученное отношение и везде (во всех кортежах), где появляется указанный в операторе номер рейса, изменить номер галереи на указанный в операторе. А требовалось всего лишь изменить один кортеж. Кроме того, информация о связи между номером рейса и номером галереи дублируется с рассмотренном отношении, что ведет к избыточности информации.
С точки зрения, как обновления, так и устранения избыточности лучше представить ту же информацию в виде базы данных из двух отношений Пилот-График и Галерея-График.
| Пилот-График | РЕЙС | ДАТА | ПИЛОТ |
| 6 июня | Иванов | ||
| 7 июня | Петров | ||
| 9 июня | Иванов |
| Галерея-График | РЕЙС | ГАЛЕРЕЯ |
При этом сохраняется возможность восстановить первоначальное отношение График из двух новых отношений. Указанной аномалии обновления больше не существует, так как нужно изменить только один кортеж, чтобы поменять назначение галереи. При этом устраняется и некоторая избыточность данных, так как каждая пара (номер рейса, номер галереи) записывается только однажды.
Вторая нормальная форма
Для данной схемы отношения R, атрибута А в Л и множества функциональных зависимостей F на R атрибут А называется первичным в R относительно F, если А содержится в каком-нибудь ключе схемы R. В противном случае А называется не первичным в R.
Ключи в этом определении не следует путать с выделенными ключами для R, так как последние могут быть на самом деле суперключами. Кроме того, могут существовать ключи для R, не являющиеся выделенными.
Пример 4. Пусть Д(РЕЙС, ДАТА, ПИЛОТ, ГАЛЕРЕЯ) и множество F ={РЕЙСДАТА → ПИЛОТ ГАЛЕРЕЯ, РЕЙС → ГАЛЕРЕЯ}.
Атрибуты РЕЙС и ДАТА являются первичными, ПИЛОТ и ГАЛЕРЕЯ - не первичными. (Допустимо, чтобы один пилот имел два рейса в день, так что ПИЛОТ ДАТА ключом не является.)
Схема отношения R находится во второй нормальной форме (2НФ) относительно множества функциональных зависимостей F, если она находится в первой нормальной форме (1НФ) и каждый непервичный атрибут полностью зависит от каждого ключа для R [14].
Схема базы данных R имеет вторую нормальную форму относительно F, если каждая схема отношения R из R находится в 2НФ относительно F.
Пример 5. Пусть R (РЕЙС, ДАТА, ПИЛОТ, ГАЛЕРЕЯ) и множество F ={РЕЙС ДАТА → ПИЛОТ ГАЛЕРЕЯ, РЕЙС → ГАЛЕРЕЯ}, R ={R}.
Схема не находится в 2НФ, так как ГАЛЕРЕЯ частично зависит от РЕЙС ДАТА. Если положить R ={(PEHC, ДАТА, ПИЛОТ); (РЕЙС, ГАЛЕРЕЯ)}, тогда схема будет находиться во второй нормальной форме. РЕЙС теперь является ключом для схемы отношения (РЕЙС, ГАЛЕРЕЯ).
Третья нормальная форма
Рассмотрим другое отношение График, представленное ниже. Предположим, что это отношение имеет ключ РЕЙС ДЕНЬ и к тому же удовлетворяет функциональным зависимостям КОД-ПИЛОТА → ИМЯ и ИМЯ → КОД-ПИЛОТА.
Если выполнить операцию обновления
ИЗМЕНИТЬ (График; 112, б июня,
КОД-ПИЛОТА=31039, ИМЯ=Иванов),
то изменяется функциональная зависимость ИМЯ → КОД-ПИЛОТА. Кроме того, имеется избыточная информация в виде пар КОД-ПИЛОТА, ИМЯ.
Проблема здесь не из-за частичной зависимости непервичного атрибута, хотя решение получается то же самое.
Это отношение можно представить в виде базы данных следующим образом.
| Пилот-График | РЕЙС | ДАТА | КОД-ПИЛОТА |
| 6 июня | |||
| 7 июня | |||
| 9 июня |
| Код | КОД-ПИЛОТА | ИМЯ |
| Иванов | ||
| Петров |
Возможность восстановления первоначального отношения сохраняется.
Перед определением третьей нормальной формы характеризуется транзитивная зависимость атрибутов.
Для данной схемы отношения R, подмножества X множества R, атрибута А в R и множества функциональных зависимостей F атрибут А называется транзитивно зависимым от X в R, если существует подмножество Y Í R, такое, что X → Y, Y не определяет функционально X, Y → А относительно F и А Ï ХY [14].
Пример 6. Пусть R (РЕЙС, ДАТА, КОД-ПИЛОТА, ИМЯ) и множество F ={PEHC ДАТА → КОД-ПИЛОТА ИМЯ, КОД-ПИЛОТА → ИМЯ, ИМЯ → КОД-ПИЛОТА}.
Атрибут ИМЯ является транзитивно зависимым от РЕЙС ДАТА, так как РЕЙС ДАТА® КОД-ПИЛОТА, КОД-ПИЛОТА не определяет функционально РЕЙС ДАТА и КОД-ПИЛОТА®ИМЯ.
Схема отношения R находится в третьей нормальной форме (ЗНФ) относительно множества функциональных зависимостей F, если она находится в 1НФ и ни один из непервичных атрибутов в R не является транзитивно зависимым от ключа для R [14].
Схема базы данных R находится в третьей нормальной форме относительно F, если каждая схема отношения R в R находится в ЗНФ относительно F.
Пример 7. Пусть R и множество F те же, что и в примере 2.10, R =(R).
Схема базы данных R не находится в ЗНФ относительно F, потому что ИМЯ является транзитивно зависимым от РЕЙС ДАТА.
Если R ={(PEHC, ДАТА, КОД-ПИЛОТА); (КОД-ПИЛОТА, ИМЯ)}, то R находится в ЗНФ относительно F.
Следует заметить, что любая схема отношения, находящаяся в ЗНФ относительно F, находится в 2НФ относительно F [14].