Определение теоретической и полной длины стрелочного перевода

L_T- теоретическая длина стрелочного перевода:

 

 

L_T =548780(0,019696-0,011031)+409090(0,071247-0,019696)+6827·0,997458=32653_мм

 

где k- прямая вставка перед математическим центром крестовины; α- угол крестовины.

 

Полной (практической) длиной L_П - называется расстояние от перед­него стыка рамных рельсов до конца крестовины и определяется по фор­муле

=32653+3611+3492=39756_мм

 

где т₁ - передний вылет рамного рельса по отношению к остряку остряка; p -хвостовой вылет крестовины.

 

Расчет осевых размеров стрелочного перевода

Имея значения марки стрелочного перевода, теоретической и полной длины, находят осевые размеры стрелочного перевода, необходимые для разбивки его на месте укладки (рис. 5.1).

 

Рис 5.1. Расчетная схема для определения осевых размеров стрелочного перевода

 

К осевым размерам стрелочного перевода относятся размеры:

5.2.1 Расстояние а - от начала рамного рельса до центра стрелочного
перевода -Ц

=39756-24772=14984_мм

5.2.2 Расстояние b - от центра стрелочного перевода - Ц до хвосто­вого стыка крестовины:

=21280+3492=24772_мм

 

 

5.2.3 Расстояние а₀ - от центра стрелочного перевода до начала остряка:

=32653-21280=11373_мм

 

 

5.2.4 Расстояние от центра стрелочного перевода до математиче­ского центра крестовины:

=1520·14=21280_мм

 

 

Определение координат для разбивки переводной кривой

Для точной постановки переводной кривой в плане рассчитывают коор­динаты переводной кривой. Координаты для разбивки переводной кривой определяются наиболее распространенным способом при котором абсциссы х прямоугольной системы координат принимают заранее равным последовательно 2,4,6,8,10,12 и т.д., а окончательную абсциссу х_к опре­деляют расчетом. За центр системы координат принимают точку на рабо­чей грани рамного рельса против корневого стыка остряка (рис.5.2). Орди­ната переводной кривой этой точке равна проекции криволинейного остряка на вертикальную ось.

 

y₀ =139.8

y₀ =548780(0.999939-0.999807)+409090(0.999807-0.999644)=139.12

 

Абсцисса конца переводной кривой равна:

 

x_k =409090 (0.071247-0.026680)=18223

x_k =32653-548780(0.019645-0.011031)-409090(0.026680-0.019645)-6827·0.997458=18238

 

α - угол крестовины; β - полный угол стрелочного перевода.

 

 

 

Рис 5.2 Расчетная схема для определения координат переводной кривой

 

Текущие координаты определятся по следующим формулам:

 

 

 

где углы находятся через по выражению:

 

Проверку конечной координаты у_к можно проверить по следующему выражению:

=1520-6827·0.071247=1033.596731

 

Расчет ведется в табличной форме.

 

 

Расчет координат для разбивки переводной кривой Таблица 1

	0.004888	0.031568	1˚48’32”	0.999501	0.000143	197.61987
	0.009777	0.036457	2˚05’21”	0.999335	0.000309	265.52881
	0.014666	0.041346	2˚22’10”	0.999144	0.0005	343.665
	0.019555	0.046235	2˚39’00”	0.998930	0.000714	431.21026
	0.024444	0.051124	2˚55’49”	0.998692	0.000952	528.57368
	0.029333	0.056013	3˚12’39”	0.998430	0.001214	635.75526
	0.034222	0.060902	3˚29’29”	0.998143	0.001501	753.16409
	0.039111	0.065791	3˚46’20”	0.997833	0.001811	879.98199
	0.044581	0.071261	4˚05’11”	0.997457	0.002187	1033.7998

 

Определение длин рельсов входящих в состав стрелочного перевода

Длины рельсов укладываемых в стрелочный перевод, определяются из элементарных геометрических расчетов. В настоящее время рамные рельсы обоих направлений стремятся делать из рельсов стандартной длины, обеспечивая при этом минимальную длину переднего вылета рам­ного рельса.

 

 

Рис 5.3. Расчетная схема для определения длин рельсов в стрелочном переводе.

 

Длины рельсов принимают стандартной длины 12,5 или 25м.

 

l₁ =39756-12123-12500-2·8+(1520+72.8/2)0.035668=15173_мм

l₄ =(409090+36,4)·(4,085616-1,528887)·3,14/180+(6827-1431)-12500-2·8=11127_мм

l₆ =32653-12500-7595-2·8-1431=11111_мм

l₇ =(409090-1520-36,4)·(4,085616-1,653944)·0,017444+6827+3492+(1520+36,4)·

· 0,035668-12500-16=15145_мм

 

где S_R - ширина колеи в середине переводной кривой. При ра­диусе переводной кривой менее 300000мм можно при­нять S_R —1524мм, а во всех остальных случаях S_R = 1520мм.

- угол соответствующий заднему стыку рамного рельса, град, опре­деляется по формуле

 

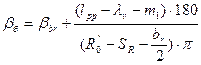
β_δ=1,125701+((12123-4756-3611)·180)/(409090-1520-72,8/2)·3,14=1,653944

ЧАСТЬ