Уравнения переноса вещества через мембрану в обратном осмосе

Как и в любом массообменном процессе, в обратном осмосе расход переходящего вещества пропорционален движущей силе и обратно пропорционален сопротивлению.

Для незаряженных мембран с достаточно высокой селективностью уравнения переноса можно записать в следующем виде:

, кг/м²с, (26)

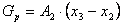, кг/м²с, (27)

Здесь G_в, G_р – соответственно удельная производительность мембраны по воде и растворенному веществу, А₁, А₂ – константы, зависящие от вида мембраны и в некоторой степени от условий проведения процесса, µ_п – вязкость пермеата, с_в – доля свободной воды в разделяемом растворе у поверхности мембраны, x₃, x₂ – соответственно концентрация растворенного вещества у поверхности мембраны со стороны разделяемого раствора и в пермеате, π₃, π₂ – соответственно осмотическое давление разделяемого раствора у поверхности мембраны и пермеата, P – разность гидростатического давления над раствором и пермеатом.

Следует заметить, что для малоселективных мембран и для мембран с большим диапазоном распределения пор по размерам, включающим неселективные и малоселективные поры, уравнения переноса изменятся, и будут включать дополнительные члены, учитывающие перенос через неселективные и малоселективные поры.

Рассмотрим величины, входящие в уравнения. В квадратных скобках заключена движущая сила для перехода воды. Об этом мы уже говорили в разделе 1 (см. уравнение 1).

Движущей силой для перехода растворенного вещества является заключенная в круглые скобки разность концентраций (x₃ – x₂).

Рассмотрим, как определяется доля свободной воды с_в. Эта величина введена в уравнение автором данного пособия исходя из предположения, что в процессе обратного осмоса через мембрану переходит только свободная вода, т.е. вода, не связанная прочно с ионами или молекулами растворенных веществ. Это предположение было экспериментально подтверждено на ацетатцеллюлозных и других типах мембран. Значение с_в находится по соотношению:

, (28)

где n - число молекул воды, прочно связанных с одной молекулой растворенного вещества или ионами, на которые молекула диссоциирует, моль воды/моль растворенного вещества, n_в = 55,56 – число молей воды в 1 литре воды, моль воды/литр воды, m₃ – концентрация растворенного вещества у поверхности мембраны, моль растворенного вещества/литр воды.

Обычно вода прочно связана в первичных гидратных оболочках ионов, но некоторые ионы, например SO₄^2-, способны удерживать воду и во вторичной оболочке.

В знаменатель дроби уравнения (23) входит также вязкость пермеата µ_п. Поток через поры может рассматриваться как Пуазейлевский, поэтому, на первый взгляд, представляется очевидным, что удельная производительность по воде обратно пропорциональна вязкости пермеата. Однако следует иметь в виду, что из-за действия поверхностных сил вязкость воды в порах обратноосмотических мембран в несколько раз больше вязкости воды в объеме. Поскольку справедливость включения µ_п в знаменатель уравнения (26) подтверждена экспериментально, остается предположить, что соблюдается пропорциональность между вязкостью воды в объеме и в порах мембраны. То есть изменение вязкости воды, связанное, например, с изменением температуры, вызывает пропорциональное изменение вязкости пермеата. При этом коэффициент пропорциональности входит в величину константы А₁.

Рассмотрим, что вообще представляют из себя константы А₁ и А₂. Само их название константами весьма условно, поскольку как мы далее увидим, они сохраняют постоянство лишь на определенных интервалах изменения переменных. Кроме того, эти константы представляют собой комплексы, включающие как те составляющие, которые способствуют переходу вещества через мембрану, так и те, которые препятствуют такому переходу.

Величина константы А₁, в первую очередь, определяется природой материала мембраны, ее пористой структурой, а также толщиной селективного слоя. А₁ тем больше, чем больше пористость мембраны, размер пор и чем меньше толщина.

Величина константы А₂ также зависит от материала мембраны, ее пористой структуры и толщины, но еще и от природы растворенного вещества. От природы мембраны, ее пористой структуры и от природы растворенного вещества зависит коэффициент распределения растворенного вещества между мембраной и прилегающим к ней раствором и коэффициент эффективной диффузии молекул либо ионов растворенного вещества в мембране. От толщины активного слоя мембраны зависит длина пути эффективной диффузии (под эффективной диффузией мы понимаем все возможные способы перехода растворенного вещества через мембрану, которые осуществляются по различным механизмам).

Константы А₁ и А₂ сохраняют постоянство в узком диапазоне изменения переменных, особенно для уплотняющихся мембран. Это связано с деформацией полимерных мембран при высоких давлениях, изменением набухаемости при изменении температуры и т.п.

Для ацетатцеллюлозных мембран можно считать, что константы постоянны при изменении концентрации электролитов от ~2·10^-4 до ~2·10^-1 моль/литр, увеличении рабочего давления до 3-5 МПа, изменении температуры от 0 до 40˚С.

Анализируя в целом уравнения переноса, можно прийти к выводу, что вода переходит через мембрану по механизму вязкого течения. Растворенные вещества переходят по механизму, близкому к диффузионному, поскольку движущей силой является разность концентраций по обе стороны мембраны. Но в целом их механизм перехода очень сложен. Он включает в себя вхождение молекул либо ионов в мембрану с некоторым коэффициентом распределения относительно концентрации у поверхности мембраны, диффузию по различным механизмам и перенос вместе с потоком пермеата. Поэтому использование уравнения (27) при количественных расчетах часто сопряжено со значительной погрешностью.

Уравнение (26) адекватно соответствует экспериментальным данным на ацетатцеллюлозных и стеклянных мембранах, однако на композитных мембранах имеет ограниченное применение, поскольку рост удельной производительности с повышением температуры более существенен, чем вытекает из уравнения (26).