Закон парности касательных напряжений

Тело находится в равновесии, если главный вектор и главный момент всех сил, приложенных к телу равны нулю:

, .

Первое условие равновесия приводит нас к уравнениям равновесия. Рассмотрим второе условие равновесия тела . Из математики известно, что момент произвольной силы – это векторное произведение плеча на силу:

,

где 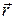- радиус-вектор точки.

Для определенности рассмотрим ДСК. Применяем ко второму интегралу теорему Остроградского-Гаусса:

.

С учетом последнего преобразования

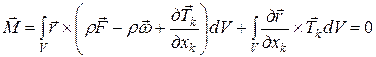. (1)

=0, из уравнения движения тела.

Учитывая, что = 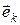, соотношение (1) преобразуется к виду:

.

Так как объем - произволен, то последнее соотношение возможно, если

=0

или

. (2)

Распишем (2) в развернутом виде. При этом учтем, что :

. (3)

Слагаемые вида тождественно равны нулю.

В силу линейной независимости векторов из соотношения (3) получаем:

закон парности касательных напряжений.

Главные деформации

Тензор деформации Коши-Грина 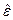- симметричный тензор второго ранга, обладает, как и тензор напряжений, определенными свойствами:

· Имеет главные значения и соответствующие им главные направления;

· Имеет инварианты;

· Тензор деформаций можно разложить на шаровую часть и девиатор.

Главное направление тензора деформаций 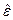- направление, вдоль которого происходит только растяжение или сжатие, а сдвиговые деформации равны нулю.

По аналогии с тензором напряжений для нахождения главных направлений необходимо решить систему

, (4)

где - скалярная величина, указывает величину относительного растяжения или сжатия, - координаты нормали, идущей вдоль искомого главного направления.

СЛАУ (4) имеет нетривиальное решение, если

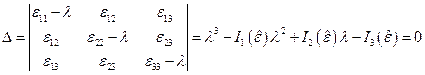, (5)

где - первый, второй и третий инварианты тензора деформаций Коши-Грина, которые пределяются следующим образом:

,

,

.

Соотношение (5) – характеристическое уравнение для тензора деформаций, имеет три действительных корня , называемых главными значениями тензора деформаций или главными деформациями. Принято обозначать эти значения , причем .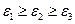

Каждой главной деформации соответствует свое главное направление. Таким образом в каждой точке тела имеется три главных направления. Таким же образом, как и для тензора напряжений, можно показать, что три главных направления взаимоортогональны в каждой точке тела.

Фиксируя в СЛАУ (4) величину и заменяя одно из уравнений (в силу их линейной зависимости) условием, накладываемым на направляющие косинусы , находим главные направления .

Инварианты тензора деформаций могут быть выражены через главные деформации следующим образом:

,

,

.

Первый инвариант в случае малых деформаций имеет определенный физический смысл. Рассмотрим элементарный прямоугольный параллелепипед в ДСК. Пусть оси СК совпадают с главными направлениями. Ребра параллелепипеда направлены вдоль осей СК. Длины ребер до деформирования равны . Так как в главных осях тензор деформаций имеет диагональную форму , параллелепипед останется прямоугольным (ребра растянутся или сожмутся, но не изменят ориентации), и после деформирования длины ребер станут равными .

Рассмотрим относительное изменение объема параллелепипеда в процессе деформирования:

В случае малых деформаций , поэтому относительное изменение объема, называемое объемной деформацией , можно записать следующим образом

.

Таким образом, объемная деформация в случае малых деформаций равна первому инварианту тензора деформаций.