Требуется определить аналитическую зависимость между численными значениями СКЗ виброскорости (V скз) и значениями вейвлет-преобразования (W) в точках максимума, то есть определить функцию:
 . (2.7)
. (2.7)
Здесь для оценки СКЗ виброскорости используется ее дискретное представление:
 (2.8)
(2.8)
где N – число отсчетов значений виброскорости в заданном промежутке времени; Vr – значение виброскорости в r -ой точке измерения [17].
Учитывая, что скейлограммы вейвлет-преобразования сигналов вибрации содержат большое количество исходных данных, а информация о виде функциональной зависимости (2.30) отсутствует, воспользуемся методикой аппроксимации указанной зависимости соответствующими линейными многообразиями в пространстве параметров V скз и W. При этом под аппроксимацией мы будем понимать восстановление функциональной зависимости по экспериментальным данным при отсутствии предположений о законах, которым подчиняется анализируемый процесс (Data-Driven).
В качестве исходных данных рассмотрим конечное множество векторов 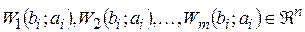 , описывающих локальные максимумы вейвлет-преобразования с координатами
, описывающих локальные максимумы вейвлет-преобразования с координатами  , для m СКЗ виброскорости.
, для m СКЗ виброскорости.
Отметим, что наиболее характерными частотами для погружного электрооборудования являются частота вращения ротора (50 Гц) и ее кратные гармоники: 25 Гц, 100 Гц, 150 Гц, 200 Гц. Скейлограмма вибросигнала с частотой 50 Гц приведена на рисунке 2.9, а векторы локальных максимумов вейвлет-преобразования для трех СКЗ виброскорости (m =3) сведены в таблицу 2.10.

Рисунок 2.8 - Скейлограмма вибросигнала с частотой 50 Гц
Таблица 2.3 - Значения вейвлет преобразования при синусоидальном сигнале с частотой 50 Гц
| № | Масштаб | Сдвиг | Значение Vскз 1,05 мм/сек | Значение Vскз 2,11 мм/сек | Значение Vскз 3,51 мм/сек |
| 1. | 11,9644 | 23,9289 | 39,8814 | ||
| 2. | 16,3379 | 32,6758 | 54,4597 | ||
| 3. | 16,7893 | 33,5785 | 55,9642 | ||
| 4. | 16,1547 | 32,3095 | 53,8492 | ||
| 5. | 16,0582 | 32,1164 | 53,5274 | ||
| 6. | 16,4654 | 32,9307 | 54,8846 | ||
| 7. | 15,8359 | 31,6718 | 52,7864 | ||
| 8. | 11,7816 | 23,5632 | 39,2719 |
В свою очередь скейлограмма вибросигнала с частотой 100 Гц приведена на рисунке 2.10, а таблица 2.11 содержит векторы локальных максимумов вейвлет-преобразования этого вибросигнала. Следует обратить внимание, что в первом случае число локальных максимумов равно 8, а во втором - 16. Аналогичные таблицы могут быть составлены и для других характерных частот.
Таблица 2.4 - Значения вейвлет-преобразования при сигнале 100 Гц
| № | Масштаб | Сдвиг | Значение Vскз 1,5 мм/сек | Значение Vскз 3 мм/сек | Значение Vскз 5 мм/сек |
| 1. | 11,92 | 23,95 | 39,9 | ||
| 2. | 16,35 | 32,69 | 54,46 | ||
| 3. | 16,84 | 33,68 | 56,11 | ||
| 4. | 16,29 | 32,58 | 54,28 | ||
| 5. | 16,06 | 32,13 | 53,52 | ||
| 6. | 16,05 | 32,11 | 53,49 | ||
| 7. | 16,07 | 32,13 | 53,53 | ||
| 8. | 16,07 | 32,13 | 53,53 | ||
| 9. | 16,07 | 32,13 | 53,53 | ||
| 10. | 16,07 | 32,13 | 53,52 | ||
| 11. | 16,04 | 32,07 | 53,43 | ||
| 12. | 15,95 | 31,9 | 53,14 | ||
| 13. | 16,07 | 32,14 | 53,54 | ||
| 14. | 16,05 | 32,99 | 54,97 | ||
| 15. | 15,86 | 31,72 | 52,84 | ||
| 16. | 11,79 | 23,59 | 39,29 |

Рисунок 2.9 - Скейлограмма вибросигнала с частотой 100 Гц.
Среди всех линейных многообразий в  найдем такое
найдем такое  , где
, где  - ортонормированные вектора, что сумма квадратов уклонений
- ортонормированные вектора, что сумма квадратов уклонений  от
от  минимальна:
минимальна:
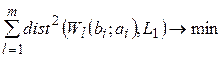 (2.9)
(2.9)
где 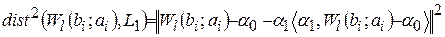 - евклидово расстояние от точки до линейного многообразия; при этом
- евклидово расстояние от точки до линейного многообразия; при этом  -евклидова норма,
-евклидова норма,  - евклидово скалярное произведение, или в координатной форме:
- евклидово скалярное произведение, или в координатной форме:

Решение задачи аппроксимации для k = 0,1 включает построение вложенных линейных многообразий  . Эти линейные многообразия определяются ортонормированным набором векторов
. Эти линейные многообразия определяются ортонормированным набором векторов  . Вектор
. Вектор  ищется, как решение задачи минимизации для
ищется, как решение задачи минимизации для  :
:
 (2.10)
(2.10)
или, что то же самое:
 . (2.11)
. (2.11)
В результате получаем, что  является выборочным средним исходных векторов
является выборочным средним исходных векторов  ,
, 
 (2.12)
(2.12)
Чтобы найти ортонормированный вектор  . централизуем вначале вектора исходных данных
. централизуем вначале вектора исходных данных  , в результате чего получаем:
, в результате чего получаем: 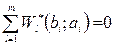 . Далее, решаем следующую задачу оптимизации:
. Далее, решаем следующую задачу оптимизации:
 . (2.137)
. (2.137)
Используя описанную методику, определим аналитическую зависимость изменения значений вейвлет-преобразования от СКЗ виброскорости для вибросигнала с частотой 50 Гц. Результаты расчетов сведены в таблицу 2.12.
На рисунке 2.11 приведены графики полученных зависимостей. Анализируя данные таблицы 2.12 и приведенные графики, можно сделать вывод о том, что все линии тренда можно разбить на 2 общие группы:
· линии тренда для масштабов 120, 122, 125, 133 и 136;
· линии тренда для масштабов 109 и 140.
Эти группы имеют близкое расположение на координатной плоскости и, следовательно, близкие аналитические описания. Разброс же в значениях между этими группами объясняется спецификой вейвлет-преобразования, а именно формой материнской функции. Такое положение вещей наблюдается при каждом вейвлет-преобразовании любого гармонического сигнала: локальные максимумы с наибольшим и наименьшим временным сдвигом резко отличаются от прочих максимумов анализируемого сигнала. Поэтому для количественной оценки степени развития дефекта погружного электрооборудования данные максимумы (вторая группа) допускается не учитывать.
Таким образом, полученные функциональные зависимости могут использоваться для выявления возможных противоречий в экспериментально полученных данных.
Таблица 2.5 - Аналитические выражения для линий тренда на частоте 50 Гц
| № | Масштаб | Сдвиг | Аналитическая зависимость |
| 1. | b 1 = 140 | а 1 = 39 |  = 11,351 VСКЗ + 0,0217 = 11,351 VСКЗ + 0,0217
|
| 2. | b 2 = 136 | а 2 = 121 | 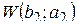 = 15,500 VСКЗ + 0,0295 = 15,500 VСКЗ + 0,0295
|
| 3. | b 3 = 133 | а 3 = 202 | 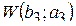 = 15,928 VСКЗ + 0,0304 = 15,928 VСКЗ + 0,0304
|
| 4. | b 4 = 125 | а 4 = 283 | 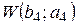 = 15,326 VСКЗ + 0,0292 = 15,326 VСКЗ + 0,0292
|
| 5. | b 5 = 122 | а 5 = 363 |  = 15,235 VСКЗ + 0,0290 = 15,235 VСКЗ + 0,0290
|
| 6. | b 6 = 122 | а 6 = 443 |  = 15,621 VСКЗ + 0,0298 = 15,621 VСКЗ + 0,0298
|
| 7. | b 7 = 120 | а 7 = 523 |  = 15,024 VСКЗ + 0,0286 = 15,024 VСКЗ + 0,0286
|
| 8. | b 8 = 109 | а 8 = 598 |  = 11,177 VСКЗ + 0,0214 = 11,177 VСКЗ + 0,0214
|
Найдем аналогичную аналитическую зависимость изменения значений вейвлет-преобразования от СКЗ виброскорости для вибросигнала с частотой 100 Гц. Результаты расчетов занесены в таблицу 2.13.
Воспользуемся полученными соотношениями, а также аналитическими зависимостями для оставшихся частот - 25 Гц, 150 Гц, 200 Гц, для оценки эффективности предложенной методики построения аналитической модели для количественного определения степени развития дефекта.

Рисунок 2.10 - Зависимости значений вейвлет преобразования от СКЗ виброскорости для вибросигнала с частотой 50 Гц.
Таблица 2.6 - Аналитические выражения для линий тренда на частоте 100 Гц
| № | Масштаб | Сдвиг | Аналитическая зависимость |
| 1. | b 1 = 70 | а 1 = 20 |  = 7,9932 VСКЗ - 0,0553 = 7,9932 VСКЗ - 0,0553
|
| 2. | b 2 = 68 | а 2 = 61 | 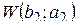 = 10,888 VСКЗ + 0,0201 = 10,888 VСКЗ + 0,0201
|
| 3. | b 3 = 66 | а 3 = 102 | 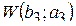 = 10,854 VСКЗ + 0,0122 = 10,854 VСКЗ + 0,0122
|
| 4. | b 4 = 63 | а 4 = 142 |  = 10,854 VСКЗ + 0,0122 = 10,854 VСКЗ + 0,0122
|
| 5. | b 5 = 63 | а 5 = 182 |  = 10,702 VСКЗ + 0,0123 = 10,702 VСКЗ + 0,0123
|
| 6. | b 6 = 63 | а 6 = 222 |  = 10,697 VСКЗ + 0,0103 = 10,697 VСКЗ + 0,0103
|
| 7. | b 7 = 63 | а 7 = 262 |  = 10,703 VСКЗ + 0,0181 = 10,703 VСКЗ + 0,0181
|
| 8. | b 8 = 63 | а 8 = 302 |  = 10,703 VСКЗ + 0,0181 = 10,703 VСКЗ + 0,0181
|
| 9. | b 9 = 63 | а 9 = 342 |  = 10,703 VСКЗ + 0,0181 = 10,703 VСКЗ + 0,0181
|
| 10. | b 10 = 63 | а 10 = 382 |  = 10,700 VСКЗ + 0,0242 = 10,700 VСКЗ + 0,0242
|
| 11. | b 11 = 63 | а 11 = 422 | 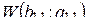 = 10,683 VСКЗ + 0,0181 = 10,683 VСКЗ + 0,0181
|
| 12. | b 12 = 63 | а 12 = 462 |  = 10,625 VСКЗ + 0,0162 = 10,625 VСКЗ + 0,0162
|
| 13. | b 13 = 61 | а 13 = 502 |  = 10,705 VСКЗ + 0,0162 = 10,705 VСКЗ + 0,0162
|
| 14. | b 14 = 61 | а 14 = 542 |  = 11,113 VСКЗ - 0,5211 = 11,113 VСКЗ - 0,5211
|
| 15. | b 15 = 60 | а 15 = 582 |  = 10,565 VСКЗ + 0,0162 = 10,565 VСКЗ + 0,0162
|
| 16. | b 16 = 54 | а 16 = 620 |  = 7,8568 VСКЗ + 0,0103 = 7,8568 VСКЗ + 0,0103
|