Задания для самостоятельной работы. ã МИЭТ, 2009

Попенко Н.И., Железнякова А.В.

Кристаллография. Методические указания по решению задач. - М.: МИЭТ, 2009. - 68 с.: ил.

Методические указания включают четыре раздела: симметрия кристаллов, определение кристаллографических индексов плоскостей и направлений в кубических и гексагональных кристаллах, кристаллохимический анализ типичных структур металлов и полупроводников, прогнозирование формы ямок травления в кристаллах. В каждом разделе изложены теоретические основы, приведены варианты контрольных работ с решениями, предложены задания для самостоятельной работы.

Предназначены для студентов факультетов ЭТМО, ЭКТ и колледжа «Электроника и информатика».

 

ã МИЭТ, 2009

Введение

Кристаллография - наука о кристаллах и кристаллическом состоянии материи. Современная техника немыслима без самого широкого использования кристаллов. В электронике находят применение проводниковые, полупроводниковые и диэлектрические кристаллы.

Кристаллография наших дней изучает законы образования, форму и структуру кристаллов, классификацию кристаллов по структурным признакам, физические свойства кристаллов. Обычно кристаллографию делят на три больших раздела:

- геометрическая кристаллография;

- химическая (кристаллохимия);

- физическая (кристаллофизика).

Реальная кристаллическая структура содержит различные дефекты, определяющие многие важные физические свойства (электрические, механические, оптические), поэтому структурные дефекты также являются предметом исследования кристаллографической науки.

Изучение традиционных разделов кристаллографии в настоящее время дополняется изучением кристаллоподобных анизотропных материалов, таких как жидкие кристаллы, текстуры, полимерные материалы, тонкие пленки, нитевидные кристаллы, а также доменной структуры сегнетоэлектриков и ферромагнетиков.

Современная кристаллография из описательной, которой она была на протяжении длительного времени, превратилась в точную науку со своим математическим аппаратом. Аналитическая геометрия кристаллического пространства, метод теории групп симметрии и метод плотнейших упаковок геометрических тел в пространстве - основные методы, используемые кристаллографией.

Несомненна практическая важность кристаллографии при решении материаловедческих и технологических задач микроэлектроники. Известные в настоящее время кристаллохимические закономерности позволяют успешно оценивать свойства материалов и целенаправленно изменять их. Поиски веществ со специальными физическими свойствами всецело базируются на кристаллохимических закономерностях.

Для решения научных и практических задач необходимо оперировать различными приемами описания симметрии и структуры кристаллов.

В данном издании рассматриваются разделы кристаллографии, связанные с симметрией, индексацией плоскостей и направлений в кубических и гексагональных кристаллах, кристаллической структурой проводниковых и полупроводниковых материалов, определением дефектности полупроводников.

Практическому освоению курса «Кристаллография» помогает теоретический материал, содержащийся в каждом разделе, и подробный разбор решений различных вариантов тестовых заданий.

Для самостоятельной работы предлагаются типовые упражнения и задачи, большинство из которых являются оригинальными.

1. Симметрические преобразования
в кристаллах

Симметрией называется особое свойство тел или геометрических фигур, при наличии которого их отдельные части могут быть условно совмещены друг с другом с помощью некоторых симметрических операций.

Симметрия характеризуется с помощью элементов и операций симметрии.

Операцией симметрии называется операция совмещения точки (или части фигуры) с другой точкой (или частью фигуры). Обе совмещаемые части фигуры симметричны.

Элементом симметрии называется воображаемый геометрический образ (точка, прямая линия, плоскость), с помощью которого осуществляется операция симметрии.

Рис.1.1. Отражение в плоскости симметрии

Различают элементы симметрии первого и второго рода. К элементам первого рода относятся плоскость симметрии, поворотные оси симметрии и центр инверсии (симметрии); к элементам второго рода - сложные элементы: инверсионные и зеркально-поворотные оси.

Плоскостью симметрии Р называется плоскость, которая делит фигуру на две зеркальные части, расположенные друг относительно друга как предмет и его зеркальное отражение (рис.1.1). Плоскость симметрии делит пополам все перпендикулярные ей прямые, соединяющие симметричные (симметрично равные) точки (части фигуры).

Поворотной осьюсимметрии
n-го порядкаL_n называется прямая линия, при повороте вокруг которой на некоторый определенный угол α = 360°/ n, именуемый элементарным углом, происходит совмещение симметричных (совместимо равных) точек (рис.1.2).

Рис.1.2. Поворотные оси симметрии

Порядок оси определяет, сколько раз произойдет совмещение симметричной фигуры с самой собой при повороте вокруг оси на 360°:

,

где a - минимальный угол поворота. Если:

a = 180°, то n = 2;

a = 120°, то n = 3;

a = 90°, то n = 4;

a = 60°, то n = 6.

Если речь идет не о кристалле, а о произвольной фигуре, порядок поворотной оси может быть любым. Так, шар имеет бесконечно большое количество поворотных осей, в том числе и бесконечного порядка L _¥ (т.е. приходит в совмещение с исходным положением при повороте на любой, в том числе и бесконечно малый угол). Правильные многоугольники с количеством сторон n имеют оси того же порядка, что и количество сторон; очевидно, что всякая прямая в любой фигуре является поворотной осью первого порядка.

В кристаллах порядок возможных поворотных осей строго ограничен. В решетчатых системах, следовательно, и в кристаллах невозможны оси пятого порядка и оси порядка выше шестого.

Центром симметрии С (центром инверсии, центром обратного равенства) называется особая точка внутри фигуры, характеризующаяся тем, что любая проведенная через нее прямая по обе стороны от нее и на равных расстояниях встречает одинаковые (соответственные) точки фигуры.

Рис.1.3. Действие центра симметрии

Операция инверсии совершается относительно точки О (рис.1.3) и представляет собой преобразование, при котором всякий вектор r, исходящий из точки О, превращается в противоположный вектор – r. Точка А ₁ может рассматриваться как зеркальное отражение точки А, полученное посредством отображения в центре симметрии С.

Из вышеизложенного вытекает следующее практически важное правило: при наличии центра инверсии каждой грани отвечает другая грань, равная и параллельная (обратно параллельная) первой.

Инверсионной осьюL_in называется прямая линия, при повороте вокруг которой на некоторый

Рис.1.4. Тригональная призма

определенный угол с последующим (или предварительным) отражением в центральной точке фигуры как в центре инверсии, фигура совмещается сама с собой.

Подобный элемент симметрии представляет как бы совокупность простой оси симметрии и центра инверсии, действующих не порознь, а совместно. Участвуя лишь в качестве составной части инверсионной оси, центр инверсии может не проявляться в виде самостоятельного элемента симметрии. Инверсионной осью обладает, например, тригональная призма (рис.1.4), явно не имеющая центра симметрии.

Прямая LL на рис.1.4 отвечает тройной оси L ₃, одновременно являющейся и шестерной инверсионной осью симметрии L_{i 6.} Действительно, после поворота вокруг оси на 60° всех частей многогранника и последующего отражения их в центральной точке фигура совмещается сама с собой.

Для кристаллов доказана возможность существования следующих инверсионных осей: L_{i 1}, L_{i 2}, L_{i 3}, L_{i 4}, L_{i 6}.

Зеркально-поворотнойосью S_n называется прямая линия, при повороте вокруг которой на некоторый определенный угол с последующим (или предварительным) отражением в перпендикулярной к ней плоскости, проходящей через центр фигуры, фигура совмещается сама с собой.

Отражение происходит в действующей совместно и нераздельно вспомогательной плоскости, которая не обязательно является плоскостью симметрии фигуры. При этом:

S ₁ = P = L_{i 2};

S ₂ = C = L_{i 1};

S ₃ = L ₃ + ^ P = L_{i 6};

S ₄ = L_{i 4};

S ₆ = L ₃ + C = L_{i 3}.

Таким образом, зеркально-поворотные оси по конечному результату их действия могут быть полностью заменены соответствующими инверсионными, и наоборот (рис.1.5).

Рис.1.5. Совмещение фигуры, обозначенной цифрой 1, с фигурой, обозначенной цифрой 2, в результате действия инверсионных или зеркально-поворотных осей

Элементы симметрии сочетаются друг с другом. Существует ряд теорем о сложении элементов симметрии, позволяющих вывести возможные совокупности элементов симметрии. Доказано, чтодва элемента симметрии влекут за собой третий равнодействующий элемент, действие которого равно сумме действий первых двух.

Теорема 1. Линия пересечения двух плоскостей симметрии всегда является осью симметрии, действие которой равно сумме действий обеих плоскостей. Элементарный угол поворота данной оси вдвое больше угла между плоскостями.

Теорема 2. При наличии двух пересекающихся осей симметрии всегда следует искать третью равнодействующую ось, проходящую через точку пересечения первых двух (теорема Эйлера).

Теорема 3а. При наличии центра симметрии С, лежащего на четной оси L _{2 n} (L ₂, L ₄, L ₆), всегда существует плоскость симметрии, перпендикулярная к L _{2 n}.

Теорема 3б. При наличии центра симметрии С и проходящей через него плоскости симметрии Р всегда существует четная ось L _{2 n}, перпендикулярная к Р.

Теорема 3в. При наличии четной оси L _{2 n} и перпендикулярной к ней плоскости симметрии Р всегда существует центр симметрии С.

Следствие. При наличии центра симметрии С сумма четных осей равна сумме плоскостей симметрии.

Теорема 4. (следствие из теоремы 2).При наличии оси симметрии L_n и перпендикулярной к ней оси L ₂ всего будет n таких осей (nL ₂):

L_n nL ₂ (^ L ₂).

Теорема 5. (следствие из теоремы 1). При наличии оси симметрии порядка n (L_n) и плоскости симметрии Р, проходящей вдоль этой оси, имеем всего n таких плоскостей (nP):

L_n nP (çç L_n).

Вид симметрии (точечная группа) - совокупность всех элементов симметрии, которыми обладает данный кристалл. Запись элементов симметрии строгая: вначале записываются оси симметрии высшего порядка, затем более низкого, далее записываются плоскости симметрии и центр симметрии.

Вид симметрии многогранников, представленных на рис.1.6, одинаков: 3 L ₄4 L ₃6 L ₂9 PC. Рассмотрим элементы симметрии гексаэдра (рис.1.6, а).

Рис.1.6. Кристаллические многогранники: а - гексаэдр (куб); б - ромбододекаэдр

Рис.1.7. Оси симметрии гексаэдра

Гексаэдр относится к кубической сингонии и обладает несколькими осями выше второго порядка. Три оси четвертого порядка 3 L ₄ (рис.1.7, а) проходят через противоположные центры граней куба. Наличие четырех осей третьего порядка 4 L ₃ - обязательный признак кристалла кубической сингонии, они проходят через противоположные вершины по пространственным диагоналям куба (рис.1.7, б). Кроме того, присутствуют шесть осей второго порядка 6 L ₂ (рис.1.7, в), которые проходят через середины противоположных ребер куба.

Плоскостей симметрии в кубе девять 9 P (рис.1.8): три проходят через середины противоположных ребер куба, а шесть - через противоположные ребра куба, включая их в себя. Кроме того, куб обладает центром симметрии.

Рис.1.8. Плоскости симметрии куба

В результате вид симметрии куба записывается следующим образом:

3 L ₄4 L ₃6 L ₂9 PC.

В табл.1.1 представлены кристаллы, относящиеся к ромбической, тригональной, тетрагональной и гексагональной сингониям.

 

Таблица 1.1

Виды кристаллов

	Пирамида	Дипирамида	Призма
Ромбическая
Тригональная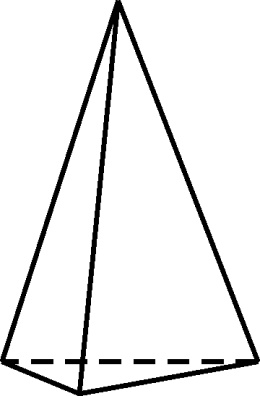

Окончание

	Пирамида	Дипирамида	Призма
Тетрагональная
Гексагональная

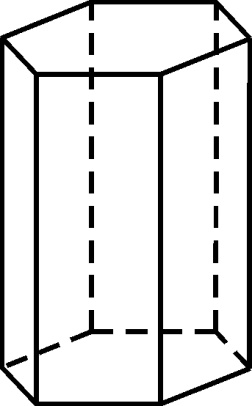
Пример решения варианта контрольной работы

1. Определить вид симметрии ромбической дипирамиды.

2. Продолжите: L_n ^ L ₂ ®

3. Как действует зеркально-поворотная ось?

4. Как располагается единичное направление в гексагональной дипирамиде?

5. Как проходят оси четвертого порядка L ₄ в кубическом кристалле?

Решение

Задание 1. При определении вида симметрии кристаллического многогранника необходимо:

1) держать кристалл в одном положении;

2) иметь в виду, что плоскости симметрии проходят через середины граней и ребер перпендикулярно им или же вдоль ребер, образуя равные углы с одинаковыми гранями и ребрами;

3) помнить о взаимодействии элементов симметрии (теоремы сложения).

Ромбическая дипирамида относится к ромбической сингонии, т.е. в ней нет осей симметрии порядка выше второго и все направления единичные.

Оси симметрии второго порядка проходят через противоположные вершины, так как при повороте на 180° кристалл самосовмещается:

 

 

.

 

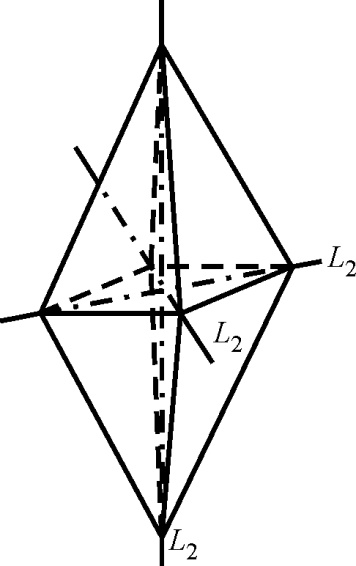
Таких осей в ромбической дипирамиде три (3 L ₂).

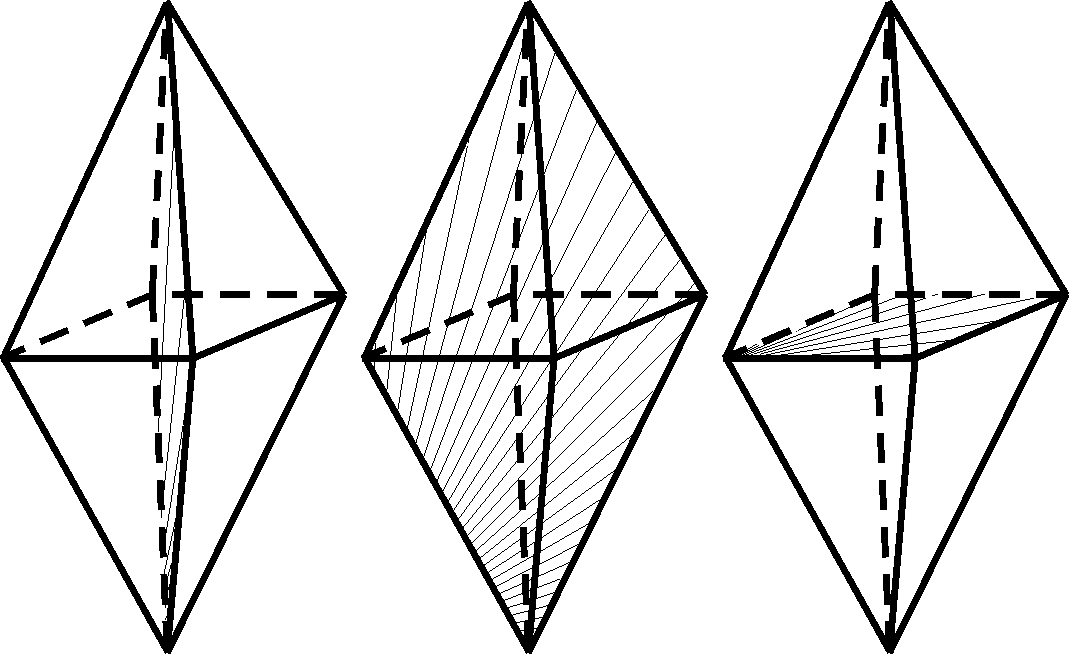
Три плоскости симметрии идут вдоль ребер (3 Р):

Есть центр симметрии С, так как по теореме L _{2 n} ^ P ® C.

Таким образом, вид симметрии ромбической дипирамиды:

3 L ₂3 PC.

Задание 2. В соответствии с теоремой 4 в присутствии оси симметрии порядка n (L_n) и перпендикулярной к ней оси L ₂ имеем всего n таких осей (nL ₂):

L_n ^ L ₂® nL ₂.

Задание 3. При действии зеркально-поворотной оси происходят отражение в плоскости симметрии и поворот на элементарный угол (180°, 120°, 90°, 60°). Следует иметь в виду, что порядок действий не имеет значения, т.е. отражение - вращение «вращение - отражение.

Задание 4. В гексагональной дипирамиде одно единичное направление, совпадающее с осью симметрии L ₆:

Задание 5. Оси четвертого порядка L ₄ в кубическом кристалле проходят через центры противоположных граней. Всего их три (3 L ₄):

Задания для самостоятельной работы

В табл.1.2 приведены исходные данные для выполнения самостоятельной работы, состоящей из трех заданий.

1. Указать плоскости симметрии кристалла.

2. Указать, как проходит поворотная ось в кристалле.

3. Определить вид симметрии кристалла.

Таблица 1.2

Исходные данные для выполнения самостоятельной работы
по теме «Симметрические преобразования в кристаллах»

Вариант	Задание 1	Задание 2	Задание 3
Ось симметрии	Вид кристалла
	Тетраэдр	L 3	Октаэдр	Гексагональная дипирамида
	Тригональная дипирамида	L 6	Гексагональная пирамида	Тетрагональная призма
	Гексагональная призма	L 4	Ромбододекаэдр	Тригональная пирамида
	Ромбическая пирамида	L 2	Ромбическая призма	Ромбододекаэдр
	Тетрагональная дипирамида	L 4	Тетрагональная пирамида	Тетраэдр
	Октаэдр	L 2	Гексагональная дипирамида	Ромбическая дипирамида
	Гексагональная дипирамида	L 3	Тетраэдр	Тригональная призма
	Тригональная пирамида	L 6	Гексагональная призма	Ромбододекаэдр
	Ромбическая призма	L 4	Октаэдр	Тетрагональная дипирамида
	Ромбододекаэдр	L 2	Тетраэдр	Тетрагональная пирамида
	Тетрагональная призма	L 2	Октаэдр	Ромбическая пирамида
	Гексагональная пирамида	L 4	Тетрагональная призма	Октаэдр

 

2. Кристаллографические индексы
плоскостей и направлений

Кристаллографические индексы плоскост ей (индексы Миллера) - это не имеющие общих множителей целые положительные или отрицательные числа, обратно пропорциональные выраженным в осевых единицах отрезкам, отсекаемым данной плоскостью на осях X, Y, Z соответственно.

Для обозначения кристаллографических плоскостей в кубических кристаллах пользуются тремя индексами (h k l). Индексы записываются и читаются поцифирно и без знаков препинания. Отрицательный знак индекса записывается над индексом (как черта сверху).

Порядок действий при определении индексов кристаллографической плоскости следующий:

1) произвести установку кристалла: определить узел расположения начала координат и направления соответствующих осей (рис.2.1). Положительными считаются концы осей:

OX - от начала координат к наблюдателю;

OY - от начала координат вправо;

OZ - от начала координат вверх.

Рис.2.1. Система координат для кубических кристаллов

При этом точка начала координат не должна принадлежать плоскости, индексы которой определяются;

2) определить в осевых единицах отрезки, отсекаемые плоскостью на координатных осях, приняв сторону элементарной ячейки за одну осевую единицу;

3) взять числа, обратные найденным отрезкам;

4) если обратные числа - целые, то сразу записать их в круглые скобки, если нет, то привести к общему знаменателю, знаменатель отбросить, а целые числа числитель записать в круглые скобки.

Нуль в символе показывает, что плоскость параллельна одной из осей, т.е. отсекает на ней бесконечно большой отрезок.

Все параллельные плоскости имеют один общий символ, так как при их параллельном перемещении пропорционально изменяются длины отрезков, отсеченных плоскостями на осях координат. Таким образом, запись (h k l) означает запись кристаллографических индексов семейства параллельных плоскостей.

Кроме параллельных плоскостей в кристаллах есть плоскости, эквивалентные кристаллографически и физически. Их индексы заключаются в фигурные скобки: { h k l }. Вся совокупность эквивалентных плоскостей может быть получена путем всевозможных перестановок положительных и отрицательных индексов.

Рис.2.2. Система координат для гексагональных кристаллов

Для обозначения кристаллографических плоскостей в гексагональных кристаллах пользуются четырьмя индексами (h k i l). Индекс i в символе плоскостей гексагональных кристаллов не является независимым, он полностью определяется остальными индексами:

i = – (h + k).

Обозначение осей в гексагональной системе показано на рис.2.2. Три оси OX, OY, OU лежат в одной (базисной) плоскости параллельно сторонам основания элементарной ячейки под углом 120° между положительными направлениями. Четвертая ось OZ перпендикулярна им и совпадает с осью шестого порядка. За единичные отрезки координатных осей OX, OY, OU принимается параметр решетки a (сторона правильного шестиугольника элементарной ячейки), оси OZ - параметр c (высота призматического ребра).

Кристаллографические индексы направлений(индексы Миллера) - это наименьшие положительные или отрицательные целые числа u, v, w, которые относятся между собой как проекции данного направления на оси OX, OY, OZ системы координат соответственно.

Индексы направления записываются в квадратные скобки [ u v w ] без знаков препинания.

Порядок действий при определении индексов направления следующий:

1) установить начало координат в узел, через который проходит интересующее направление. Если направление не выходит из узла и не входит в него, то оно переносится параллельно себе так, чтобы оно входило или выходило из узла;

2) найти проекции направления на координатной оси;

3) заключить в квадратные скобки полученные значения проекций, если они целые числа; если значения проекций - дробные, то привести их к наименьшим целым числам, после чего заключить в квадратные скобки [ u v w ].

Отрицательные значения проекций на любую координатную ось имеют отрицательный индекс и отмечаются чертой над соответствующим индексом.

Символ [ u v w ] обозначает семейство параллельных направлений. Все направления, параллельные данному, имеют те же индексы.

Совокупность эквивалентных направлений, которые могут совместиться друг с другом с помощью преобразований симметрии, свойственных данному классу симметрии, пишется в угловых скобках < u v w >.

При определении индексов направлений в гексагональных кристаллах используется система координат, приведенная на рис.2.2.

В символе направлений [ u v i w ] первые три индекса также взаимозависимы:

i = – (u + v).

Запись [ u v i w ] обозначает не только одно направление, но и все семейство параллельных направлений.

Для кристаллов кубической сингонии существует ряд формул, позволяющих рассчитывать геометрические соотношения между плоскостями и направлениями, зная их кристаллографические индексы:

1. Определение расстояния между плоскостями, входящими в одно семейство параллельных плоскостей (h k l):

,

где a - параметр решетки кристалла.

2. Вычисление угла j между кристаллографическими плоскостями (h ₁ k ₁ l ₁) и (h ₂ k ₂ l ₂) и направлениями [ u ₁ v ₁ w ₁] и [ u ₂ v ₂ w ₂]:

3. Определение принадлежности направления с индексами [ u v w ] плоскости (h k l). Если направление [ u v w ] принадлежит плоскости
(h k l), то справедливо следующее соотношение:

hu + kv + lw = 0.

4. Нахождение индексов линии пересечения двух плоскостей [ u v w ]:

u = k ₁ l ₂ – k ₂ l ₁.

v = l ₁ h ₂ – l ₂ h ₁.

w = h ₁ k ₂ – h ₂ k ₁.

Существует мнемоническое правило для запоминания порядка букв и индексов в указанных выше равенствах. Запишем два набора индексов Миллера следующим образом:

Проведем вертикальные линии, как показано на схеме, и зачеркнем крайние четыре индекса. Перемножим попарно оставшиеся индексы в соответствии со стрелками и возьмем произведения со знаком «плюс», если стрелка направлена слева направо, и со знаком «минус», если она направлена справа налево:

.

2.1. Обозначение плоскостей и направлений
в кубических кристаллах

Контрольные работы для различных групп и факультетов отличаются набором заданий. Приведенный первый вариант дается группам, наиболее подробно изучающим кристаллографию, и содержит все возможные задания по данной тематике. Два остальных варианта содержат выборочно задания, приведенные в первом варианте, поэтому примеры их решения не приводятся. Для самостоятельной подготовки к контрольной работе приводятся исходные данные и набор заданий.

Пример решения варианта контрольной работы

Вариант 1

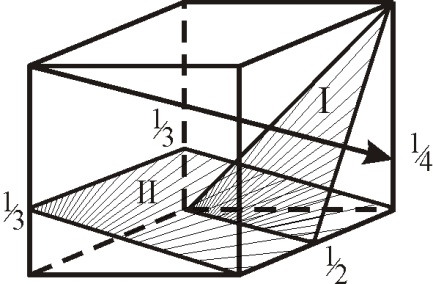
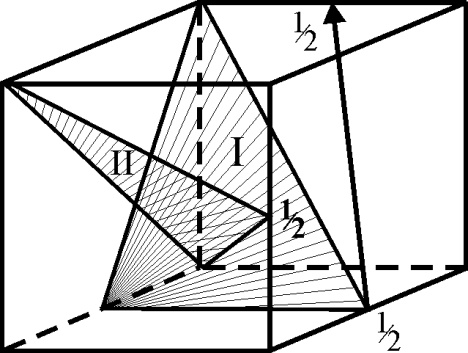
1. Определить кристаллографические индексы плоскости I.

2. Плоскость отсекает отрезки на осях: OX = –1/2, OY = –1/3, OZ = –1. Построить плоскость и определить кристаллографические индексы.

3. Определить расстояние между плоскостями семейства II.

4. Определить индексы плоскостей и число семейств плоскостей, входящих в совокупность {301}.

5. Определить кристаллографические индексы выделенного направления.

6. Проекции направления на координатные оси равны соответственно: OX = 1/2, OY = –1, OZ = 1. Построить направление и определить кристаллографические индексы.

7. Определить кристаллографические индексы направления линии пересечения плоскостей (110) и (112).

8. Определить индексы направлений и число семейств направлений, входящих в совокупность <121>.

9. Установить принадлежность направления [210] плоскости (001).

10. Определить угол между плоскостями (221) и (110).

Решение

Задание 1. Установим начало координат, определим отрезки, отсекаемые плоскостью на координатных осях, и возьмем числа, обратные данным отрезкам:

	X	Y	Z
	–1
	–1

Задание 2. Построим заданную плоскость в пределах элементарной ячейки и определим кристаллографические индексы:

 

	X	Y	Z
–	–	–1
–2	–3	–1

 

Задание 3. Установим начало координат, определим отрезки, отсекаемые плоскостью на координатных осях, и возьмем числа, обратные данным отрезкам:

 

	X	Y	Z	(013)
¥

Расстояние между плоскостями, входящими в одно семейство параллельных плоскостей, можно определить по формуле

следовательно,

.

Задание 4. Произведем все возможные перестановки индексов, придав им и отрицательные значения:

(301)	()	()	( ]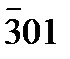
(103)	()	()	()
(013)	()	()	()
(031)	()	()	()
(130)	()	()	()
(310)	()	()	()

Число плоскостей, входящих в совокупность, равно 24, число семейств плоскостей в два раза меньше, так как плоскости попарно параллельны, - 12.

Задание 5. Установим начало координат в начало направления и определим проекции направления на координатные оси:

 

 

	X	Y	Z	[ ]
–1		–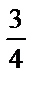
–4		–3

Задание 6. Построим заданное направление в пределах элементарной ячейки и определим кристаллографические индексы направления:

	X	Y	Z	[ ]
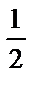
	–1
	–2

Задание 7. Такая задача может быть решена с помощью перекрестного умножения. Необходимо записать дважды индексы заданных плоскостей друг под другом, отбросить оба крайних столбца, перемножить попарно индексы по схеме:

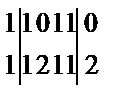
Индексы линии пересечения [ u v w ] - .

Поскольку кристаллографические индексы направления – это наименьшие целые числа, то правильная запись индексов направления .

Задание 8. Произведем все возможные перестановки индексов, придав им и отрицательные значения:

[121]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]
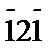[211]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]
[112]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]	[ ]

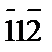Число направлений, входящих в совокупность, равно 24, число
семейств - 12.

Задание 9. Условие принадлежности направления данной плоскости имеет вид:

.

Исходя из этого, 0×2 + 0×1 + 1×0 = 0, т.е. направление принадлежит данной плоскости.

Задание 10. Угол между плоскостями (h ₁ k ₁ l ₁) и (h ₂ k ₂ l ₂) определяется по формуле

.

Угол между плоскостями (221) и (110):

.

 

Вариант 2

1. Определить кристаллографические индексы плоскости I и расстояние между плоскостями семейства I.

2. Определить кристаллографические индексы плоскости II и эквивалентные плоскости, входящие в совокупность плоскостей II.

3. Плоскость отсекает отрезки на осях: OX = 1/3, OY = ¥, OZ = –1. Построить плоскость и определить кристаллографические индексы

4. Определить кристаллографические индексы выделенного направления и принадлежность направления плоскости .

5. Определить кристаллографические индексы семейства направлений, параллельных линии пересечения плоскости I и (100), и угол между плоскостями I и .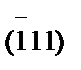

Вариант 3

1. Определить кристаллографические индексы плоскости I и расстояние между плоскостями семейства I.

2. Определить кристаллографические индексы плоскости II и число эквивалентных плоскостей, входящих в совокупность плоскостей II.

3. Определить кристаллографические индексы выделенного направления.

4. Определить кристаллографические индексы семейства направлений, параллельных линии пересечения плоскости I и .

5. Установить принадлежность направления [310] плоскости (001).