Кристаллохимические задачи

Задача 1. Определить расстояние между наиболее плотноупакованными плоскостями в решетке алюминия, если известны его атомная (26,98) и удельная (2,70 г/см³) массы.

Решение

Кристаллическая структура Al - ГЦК. В кубических кристаллах расстояние между плоскостями, входящими в одно семейство параллельных плоскостей, определяется из соотношения

,

где a - параметр решетки алюминия; (h k l) - индексы плоскости.

Для Al , так как {111} - совокупность наиболее плотноупакованных плоскостей.

Удельная масса определяется по формуле

,

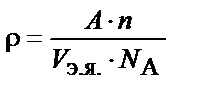где A - атомная масса; n - число атомов в элементарной ячейке;
V _э.я. - объем элементарной ячейки; N _A = 6,02·10²³ ат./см³ - число Авогадро.

Для алюминия n = 4, V _э.я. = a ³, тогда

.

Из данного выражения можно получить значение параметра кристаллической решетки Al:

.

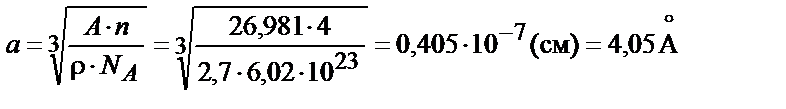Следовательно,

Ответ:

Задача 2. Определить объем элементарной ячейки меди, параметр ее решетки а и радиус атома R, если известно, что медь имеет ГЦК решетку, атомную массу А = 63,5 и удельную массу r = 8,88 г/см³.

Решение

V _э.я. - объем элементарной ячейки; N _A = 6,02·10²³ ат./см³- число Авогадро.

Отсюда

Для определения радиуса R атома меди рассматриваем наиболее плотноупакованное направление [110], вдоль которого происходит касание атомов: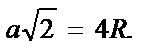

Определяем параметр решетки и радиус атома

Ответ: V _э.я. = 4,75·10^-23 см³, a = 3,62·10^-8 см и R = 1,28·10^-8 см.

Задача 3. Определить атомную массу α-Fe, имеющего ГЦК решетку, если известны его удельная масса (7,87 г/см³) и радиус атома (0,124 нм).

Задача 4. Определить удельную массу платины по известному параметру решетки (3,93 ) и атомной массе (195,09).

Задача 5. Определить объем элементарной ячейки решетки кадмия по известным удельной (8,65 г/см³) и атомной (112,40) массам.

Задача 6. Определить параметр решетки бария по известным удельной (3,65 г/см³) и атомной (137,34) массам.

Задача 7. Определить радиус атома молибдена по известным удельной (9,01 г/см³) и атомной (95,94) массам.

Задания для самостоятельной работы

1. Определить число атомов в элементарной ячейке.

2. Определить координационное число и радиус первой координационной сферы в структуре.

3. Построить плоскость в элементарной ячейке и определить ее ретикулярную плотность.

4. Построить направление в элементарной ячейке и определить его ретикулярную плотность.

5. Определить коэффициент заполнения пространства и долю объема, приходящуюся на тетраэдрические и октаэдрические пустоты в элементарной ячейке.

Исходные данные для выполнения заданий приведены в табл.3.1.

Таблица 3.1

Исходные данные для выполнения самостоятельной работы по теме «Кристаллохимический анализ типичных структур металлов»

Вариант	Задание
(h k l)	Me	[ u v w ]	Me
	Mg	W		α-Fe		Cu	Ti
	Al	Zn		Ag		Mo	Cu
	Mo	Pt		Al		Mg	Zn
	Au	α-Fe		Mo		α-Ti	Cr
	Zn	γ-Fe		Mg		Cd	Cd
	Cu	β-Po		Zn		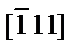Ba	Nb
	W	Be		Al		Cr	Mg
	Cr	Cd		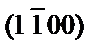Be		γ-Fe	Au
	Ti	Mo		W		Zn	W
	Ag	Mg		Au		Al	Be
	Cd	Ca		Pt		β-Po	Al
	Pt	Zn		γ-Fe		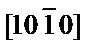Be	β-Po