1. Собрать схему по рис.29 без нулевого провода. Для симметричной нагрузки установить сопротивления R по 1кОм. Для исследования несимметричной нагрузки установить в фазе В сопротивление 470 Ом.
 |
2. Произвести измерения параметров и записать показания приборов в табл. 12.
3. Подключить нулевой провод и повторить измерения с сопротивлениями, приведенными в п.1.
4. Произвести необходимые вычисления и записать в табл.12.
5. Построить векторную диаграмму для режима, указанного преподавателем.
Контрольные вопросы
1. Какой ток больше в схеме «звезда» - линейный или фазный?
2. Какое напряжение больше - линейное или фазное в схеме «звезда» при симметричной нагрузке? Во сколько раз больше?
3. Изменяются ли напряжения на нагрузке при нарушении симметрии в схеме без нулевого провода?
4. Что нужно сделать для выравнивания напряжений при симметричной нагрузке в схеме без нулевого провода?
5. Изменяются ли напряжения на нагрузке при нарушении симметрии в схеме без нулевого провода?
6. Какая система (трёхпроводная или четырёхпроводная) используется в жилых помещениях?
7. Какие провода вводят в квартиру (два фазных или два нулевых или фазный и нулевой)?
8. В каком проводе следует устанавливать выключатель (фазном или нулевом)?
Таблица 12
| Параметры | Без нулевого провода | С нулевым проводом | ||||
| RB = ¥ | RB = R | RB = 1/2R | RB = ¥ | RB = R | RB = 1/2R | |
| Источник питания | ||||||
| UAB, В | ||||||
| UBС, В | ||||||
| UCA, В | ||||||
| UAN, В | ||||||
| UBN, В | ||||||
| UCN, В | ||||||
| Приемник | ||||||
| UA01, В | ||||||
| UB01, В | ||||||
| UC01, В | ||||||
| U001, В | ||||||
| IA, мА | ||||||
| IB, мА | ||||||
| IC, мА | ||||||
| I0, мА | ||||||
| Вычислить | ||||||
| ||||||
| ||||||
|
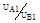
Работа № 7. Переходные процессы в цепи постоянного тока
Цель работы – исследование переходных процессов при коммутации цепей постоянного тока с элементами R, L и C.
Программа работы
1. Определение влияния элементов цепи на переходный процесс.
2. Расчёт тока и напряжения в цепи с индуктивность или ёмкостью по заданию преподавателя.
3. Экспериментальное исследование переходных характеристик тока и напряжения.
4. Определение времени процесса по опытным данным.
Общие положения
Переходные процессы - это процессы перехода от одного установившегося состояния к другому установившемуся состоянию. Изменения параметров элементов схемы или изменение режима работы самой схемы называются коммутациями.
В природе соблюдается принцип непрерывности во времени потокосцепления индуктивности и электрического заряда ёмкости.
; 
. 
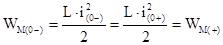Законы коммутации
1-й закон: Потокосцепление скачком измениться не может:
Следствие: В первый момент после коммутации ток в катушке индуктивности скачком измениться не может
.
2-й закон: Заряд ёмкости скачком измениться не может:
q(0+) = q(0-).
Следствие: В первый момент после коммутации напряжение на ёмкости скачком измениться не может
.
На основании законов коммутации определяется постоянная интегрирования свободной составляющей тока или напряжения при расчете переходных процессов. За начало отсчета переходного процесса принимается время равное нулю.
Анализ переходных процессов в линейных цепях с сосредоточенными параметрами сводится к решению линейных неоднородных дифференциальных уравнений, составленных на основе законов Кирхгофа для после коммутационного процесса.
При включении цепи R, L на постоянное напряжение (рис.30):
.
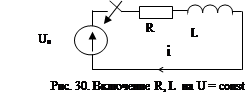
Общее решение такого уравнения может быть найдено методом наложения принуждённого и свободного режимов:
; 
,
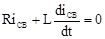где 
- ток принуждённого режима при 
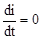или частное решение неоднородного уравнения. Принуждённый режим определяет новое состояние электрической цепи после окончания переходного процесса;
- ток свободного режима или общее решение однородного уравнения (с нулевой правой частью).
До коммутации (до включения) ток в цепи отсутствовал 
. На основании 1-го закона коммутации можно записать 
, т.е. ток в индуктивности в первый момент после коммутации равен току до коммутации. После коммутации переходный процесс описывается дифференциальным уравнением 
. Свободную составляющую определяем из уравнения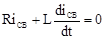 
. Решение этого уравнения 
;
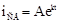k - корень характеристического уравнения 
;
где 
;
А - постоянная интегрирования, определяемая из начальных условий при t = 0 на основании Первого закона коммутации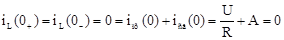 
,
, отсюда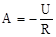 
.
Решение:
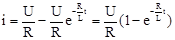
Напряжение на R: 
.
Напряжение на L: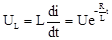 
.
Кривые тока и напряжения на индуктивности при включении R, L на U=const приведены на рис.31.
При включении цепочки R, C на постоянное напряжение (рис.32) уравнение переходного процесса примет вид:
, где 
.
 |
После подстановки получим выражение 
. Решим уравнение относительно UC:
; 
; 
.
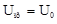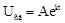Докоммутационный режим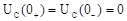 
. Характеристическое уравнение 
; 
.
А - постоянная интегрирования, определяемая из начальных условий при t = 0:
.
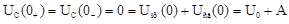Отсюда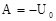 
.
Решение: 
и 
.
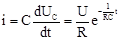Кривые тока и напряжения на конденсаторе при включении R, С на U=const приведены на рис. 33.