В основу теплового расчета положена методика, рассмотренная в [1] для установившегося теплового режима изоляции. Так как аксиальные размеры изолятора значительно больше радиальных, то при проведении теплового расчета принимают, что вся теплоотдача осуществляется только в радиальном направлении. Для проведения расчета задают ряд значений температуры стержня Тс (40, 60, 80, 100ºС) и максимальную температуру окружающей среды Т0 max. Для каждого значения температуры стержня порядок расчета следующий:
1. Расчет тепловых сопротивлений
- тепловое сопротивление масляной прослойки
,
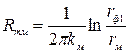где kм= 0,2 Вт/м·ºС – коэффициент теплопроводности масла; rф1=rм+(6..10 мм) – внутренний радиус фарфоровой покрышки; rм – радиус последней конденсаторной обкладки.
- тепловое сопротивление фарфоровой покрышки
,
где kф= 0,8 Вт/м·ºС – коэффициент теплопроводности фарфора; rф2=rф1+30 мм – внешний радиус фарфоровой покрышки.
- эквивалентное тепловое сопротивление, учитывающее теплоотдачу с поверхности фарфора в окружающую среду
,
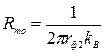где kв=20 Вт/м2·ºС – коэффициент теплоотдачи с поверхности фарфора в воздух.
2. Расчет потерь в токоведущем стержне
Активное сопротивление стержня на единицу его длины при температуре То
,
где ρ =0,0175 Ом·мм2/м– удельное объемное сопротивление материала стержня (медь); 
– сечение стержня.
Потери в токоведущем стержне
,
где α=0,0039 1/ºС – температурный коэффициент сопротивления материала (медь) стержня.
3. Расчет потерь в k-м слое изоляции
Емкость слоя
=С=const
Потери в k-м слое изоляции
,
,
где ΔUi2 – падение напряжения на i-ом слое при наибольшем рабочем напряжении; Сi´ - емкость i-го слоя на единицу его длины; tgδi – определяется по кривой tgδ=f(Т) (рисунок 2) для температуры i-го слоя (для первого слоя Т1≈Тс).
Рисунок 2 –Зависимость tg δ от температуры для бумажно-масляной изоляции
4. Тепловое сопротивление k-го слоя на единицу длины
где 
Вт/(м ·°С) коэффициент теплопроводности бумажно-масляной изоляции
Перепад температур в слоях изоляции
Температура слоя
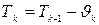
5. Температура внешней поверхности бумажно-масляной изоляции Ти равна температуре последнего слоя изоляции Тм
Полный тепловой поток, подходящий в единицу времени к внешней изоляции и проходящий через остальные элементы цилиндрической системы изолятора Qи равен тепловому потоку последнего слоя изоляции Qм
7. Расчет количества тепла, отводимого от наружной поверхности изоляции в окружающую среду
8. Таким образом, в результате первого этапа расчета для принятой температуры стержня (например, Тс =40 ºС) определены значения Qи , Qотв и Ти. Аналогичные расчеты проводятся для остальных температур стержня (60, 80, 100 ºС) и определяют соответствующие им значения Qи , Qотв и Ти.
9. Построение графика зависимости тепловыделений и теплоотдачи от температуры наружной поверхности изоляции и определение точки теплового равновесия.
По полученным данным (4 точки) Qи , Qотв и Ти строится зависимость Qи=f(Tи) и Qотв=f(Tи). Взаимное расположение кривых тепловыделения и теплоотдачи показано на рисунке 3.
Если кривая тепловыделения пересекает прямую теплоотдачи (пересечение обязательно в двух точках), то точкой устойчивого равновесия является нижняя точка пересечения А и устойчивое состояние возможно. Чем дальше отстоят обе точки
 |
Рисунок 3 – Диаграмма для расчета тепловой устойчивости изолятора конденсаторного типа
пресечения, тем надежнее работа изолятора, так как тем меньше будет возможность развития теплового пробоя вследствие некоторого ухудшения изоляции в процессе эксплуатации. Если прямая теплоотдачи пройдет ниже кривой тепловыделения, не пересекая последнюю, то тепловое равновесие невозможно и имеет место тепловой пробой изолятора.
При отсутствии устойчивого теплового равновесия необходимо произвести изменения в конструкции изолятора и затем повторно проверить его тепловую устойчивость.