Расчет внутренней изоляции

Расчет проводится для наиболее нагруженного слоя. Механическое напряжение в изоляции предполагается равным нулю.

 

1. Вероятность безотказной работы одного из слоев при равновероятном отказе любого из них

,

где Р(τ) – вероятность безотказной работы изолятора; Р_k(τ) – вероятность безотказной работы одного слоя; m – число слоев изоляции.

2. Функция распределения наибольших значений y

,

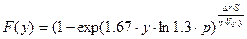где S- площадь наиболее нагруженного слоя

η – коэффициент неравномерности поля

i – номер слоя (первый или последний).

Остальные параметры, входящие в уравнение определяют по таблице 2

Таблица 2 – Параметры уравнения «кривой жизни»

 

, Дж	, Дж·м/В	,
5,5·10-19	4·10-27	0.001		0.15	2·10-7

 

 

3. Число рядом расположенных неоднородностей y. Задаваясь рядом значений y, определяют значения функции F(y), строят зависимость F(y) и по полученному графику определяют искомое y при F(y)= Р_k(τ) (рисунок 4)

 

 

Рисунок 4 – Подбор значения y

4. Коэффициент неоднородности электроизоляционного материала

g_*- относительная проводимость неоднородности (таблица 2).

 

5. В эксплуатационных условиях электрическая изоляция подвергается действию постоянных, переменных и случайных нагрузок. Если старение изоляции в эксплуатации не имеет особого значения, то для расчета времени до ее отказа несущественно, в каком порядке действует нагрузка.

Так как случайные нагрузки (в данном случае перенапряжения) являются непрерывными, то их необходимо заменить дискретными следующим образом:

5.1 Определяется нижняя граница диапазона нагрузок

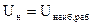
5.2 Определяется верхняя граница диапазона нагрузок

где k=1,2 – 1,3

5.3 Полученный диапазон разбивается на n=10 – 15 интервалов, определяются ширина

и границы U_i-1; U_i каждого интервала.

5.4 Определяется середина каждого интервала

5.5 Рассчитывается значение функции распределения вероятностей перенапряжений F(U^*_i) для нормального закона

где М(U) – математическое ожидание

- интеграл Лапласа.

Определяется приращение функции на интервале

Напряженность поля при действии перенапряжений

где = Е_rдоп - максимальная радиальная напряженность при расчетном напряжение U_р= U_{наиб.раб}

при действии рабочих напряжений

Е_i=Е_раб.

 

 

Относительное время действия перенапряжения

где N – число перенапряжений в год; 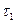- продолжительность одного перенапряжения, с; - продолжительность года, с.

Рассчитанные значения можно представить в виде таблицы 3.

Таблица 3 – Расчет случайной нагрузки

j

Ui-1, кВ

Uj,кВ

Ui*, кВ

F(Ui*)

∆F(Ui*)

ηEi

τi/τj

 

6. По заданному исполнению и категории размещения по таблице 3-1 [2] выбирается диапазон рабочих температур (верхнее Т_в и нижнее Т_н значения).

7. Полученный диапазон разбивается на n=10 – 15 интервалов, определяются ширина

и границы Т_i-1; Т_i каждого интервала.

8. Определяется середина каждого интервала

9. Строится годовой график температур (рисунок 5) и определяются продолжительности действия средних температур в году (в днях и секундах).

10. Для полученных средних температур окружающей среды определяем соответствующие температуры изоляции

,

где Q_отв – определяются по графику тепловой устойчивости для точки А.

При расчете учитываются только те , для которых можно выполнить следующие построения. На оси Т_и графика тепловой устойчивости откладывается и через эту точку проводится прямая параллельная Q_отв. Если данная прямая имеет пересечение с кривой Q_и, то средняя температура окружающей среды используется при расчете температуры изоляции Т_i.

Количество полученных температур m.

 

Рисунок 5 – Распределение годовой температуры по месяцам

 

11. Рассчитанные значения можно представить в виде таблицы 4.

Таблица 4

 

j

Диапазон измерения

Ср. темп

Время действия T, дни

Время действия Т, сек

Ti, К при 20С

 

12. Определяется вероятность разрыва связи в единицу времени при действии рабочих напряжений q_i и действии перенапряжений q_ij с учетом действия температур Т_i, К

где φ(х) - функция нагрузки, действующей на связь

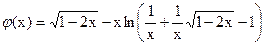
х - безразмерная характеристика нагрузки

 

13. Расчет времени до отказа

Расчет внешней изоляци

1. Вероятность пробоя изоляции при одном перенапряжении

где Q(U_пер) – функция распределения вероятностей амплитуд перенапряжений при напряжении перекрытия

Амплитудное значение напряжения перекрытия

Разбиваем промежуток () на n интервалов с шагом ΔU_пер=10кВ и для каждого значения рассчитываем Q(U_перi) и f(U_перi):

,

где М(U_пер) – математическое ожидание перекрытий

;

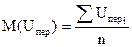σ-среднеквадратичное отклонение

f(U_пер) - функция плотности распределения вероятностей перекрытий

2. Вероятность отсутствия перекрытия за τ лет

 

3. Вероятность перехода перекрытия в дугу:

4. Вероятность разрушения изолятора дугой принимается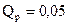

Тогда вероятность разрушения изолятора в результате перекрытия:

5. Вероятность безотказной работы фарфоровой покрышки:

Вероятность безотказной работы изолятора

 

Литература

1. Кучинский Г.С. Расчет проходных изоляторов конденсаторного типа. Учебное пособие.- Л.: изд. ЛПИ, 1983

2. Дмитриевский В.С. Расчет и конструирование электрической изоляции: Учебное пособие для вузов. – М.: Энергоиздат, 1981

 

ВАРИАНТЫЗАДАНИЙ

для курсового проекта по дисциплине«Эксплуатация, диагностика и ремонт электрооборудования ЭЭС» профиль подготовки 140400.68 – Электрические станции, системы и сети

№ варианта	Тип изоляции	Номинальное напряжение, кВ	Номинальный ток нагрузки, А	Исполнение, категория размещение	Вер-ть безотказной работы внутр. из-ии	Число перенапряжений в год	Продолжит. одного перенапр., с
	БМИ			ХЛ, 1	0,8		0,004
	БМИ			ТВ, 1	0,98		0,003
	БМИ			У, 1	0,99		0,005
	БМИ			ТС, 1	0,992		0,006
	БМИ			Т, 1	0,985		0,003
	БМИ			О, 1	0,97		0,004
	БМИ			Т, 1	0,99		0,005
	БМИ			В, 1	0,975		0,004
	БМИ			ХЛ, 1	0,98		0,003
	БМИ			У, 1	0,96		0,002
	БМИ			О, 1	0,995		0,006
	БМИ			В, 1	0,996		0,004
	БМИ			ТС, 1	0,95		0,003
	БМИ			В, 1	0,975		0,005
	БМИ			О, 1	0,99		0,003
	БМИ			ХЛ, 1	0,986		0,004
	БМИ			У, 1	0,964		0,004
	БМИ			У, 1	0,995		0,006
	БМИ			ТВ, 1	0,98		0,005

Вариант выбирается по сумме двух последних цифр номера зачетной книжки.