Количественный анализ кинетических закономерностей топохимических реакций, том числе реакций диссоциации, очень сложен. Однако, рассмотрев несколько идеализированных случаев диссоциации, можно выяснить влияние ряда факторов на кинетику рассматриваемого процесса. Для реакций твердого тела с газообразным реагентом получили распространение относительно простые выражения, отражающие те или иные особенности реакции на различных этапах ее протекания.
Одним из этих выражений является уравнение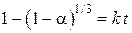 
, соответствующее модели сжимающегося (уменьшающегося) объема исходной фазы. В ней предполагается быстрое и сплошное зародышеобразование и последующее увеличение границы раздела и продвижение ее в объем старой фазы. Эта модель применяется также для описания кинетики реакции на заключительном этапе (после максимума скорости реакции) при отсутствии диффузионных торможений в слое твердых продуктов.
Кинетика процесса, протекающего в диффузионном режиме, может быть описана уравнением 
.
Нередко при анализе кинетики диссоциации применяют уравнение Ерофеева – Колмогорова в виде 
или чаще в логарифмической форме
.
Выводы указанных и некоторых других уравнений, а также обсуждение с их помощью некоторых экспериментальных данных по диссоциации соединений приведены в нижеследующих упражнениях и примерах.
Упражнение 3.1. На основе общих положений химической кинетики обратимых адсорбционно-химических реакций получить кинетическое уравнение для описания скорости процесса диссоциации карбоната в кинетическом режиме.
Решение. Если процесс не лимитируется сложной в кинетическом описании кристаллохимической стадией зарождения новой фазы, то обратимую реакцию диссоциации - образования карбоната можно представить схемой
Скорость ее равна:
,
где 
и 
– константы скорости прямой и обратной реакций.
Уравнение можно записать в виде:
.
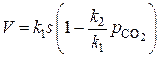Для равновесия 
и 
. Тогда из равенства
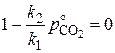
следует, что
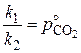и 
.
Приняв
,
получим
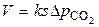. (3.1)
Полученное уравнение показывает, что скорость процесса определяется величиной реакционной поверхностью, температурой и степенью химического пересыщения 
.
Упражнение 3.2. Исходя из допущения о сферической форме частиц диссоциирующего соединения, получить кинетическое уравнение зависимости степени превращения от времени для процесса, протекающего в кинетическом режиме.
Решение. Если исходное соединение состоит из частиц сферической формы с начальным радиусом 
и имеет массу 
, то к моменту времени t произойдет изменение массы 
и радиуса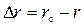 
, где m и r – масса материала и радиус частиц к моменту времени t. Тогда степень превращения 
исходного вещества 
. Для каждой из частиц 
, где 
– плотность вещества. Подставляя m и в выражение для , получаем
(3.2)
Скорость процесса V, выраженная через изменение количества (моль) исходного вещества в единицу времени
(3.3)
где M – молярная масса вещества.
Сравнивая полученное выражение с уравнением (3.1) для скорости процесса в кинетическом режиме и учитывая в последнем 
, получим
и 
.
При постоянных значениях температуры (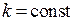
), давления 
и молярного объема 
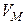скорость уменьшения размера непрореагировавшей части исходного соединения постоянна, то есть линейная скорость 
. После интегрирования этого уравнения от 0 до t и от r o до r получаем 
. Отсюда относительная толщина слоя продукта
.
Записав отношение размера непрореагировавшей части исходного соединения к начальному размеру через степень превращения, приходим к уравнению
.
Это уравнение, приведенное к форме
,
известно как закономерность модели сжимающегося объема или как уравнение Мак-Кевана. Оно предполагает быстрое образование границы раздела фаз с последующим линейным во времени продвижением реакционной зоны в объем разлагающегося кристалла.
Для полного завершения диссоциации (
) требуется время
(3.4)
Оно, как видно, уменьшается с уменьшением размера частиц материала, с ростом температуры (что соответствует увеличению константы скорости), с уменьшением фактического парциального давления газа в реакторе (что соответствует увеличению 
).
Упражнение 3.3. На основе общих положений диффузионной кинетики получить кинетическое уравнение для описания скорости процесса диссоциации карбоната в диффузионном режиме. Исходя из допущения о сферической форме частиц соединения, получить уравнение зависимости степени превращения от времени для процесса, протекающего в диффузионном режиме.
Решение. Если в процессе диссоциации продукт оказывается малопористым, плотным, то имеются значительные диффузионные торможения, и процесс может осуществляться в диффузионном режиме. Адсорбционно–кристаллохимические реакции идут быстро, и поэтому в порах на границе раздела фаз устанавливается давление, близкое к равновесному 
, и соответствующая ему концентрация газа 
. На наружной поверхности частично прореагировавшего зерна устанавливается концентрация 
, соответствующая давлению 
в объеме газа при отсутствии внешнедиффузионных торможений.
Скорость диффузии газа через слой оксида в соответствии с законом Фика
,
где D – коэффициент диффузии газа.
Для процесса со сферической формой частиц
(3.5)
где 
– радиус сферы в слое оксида, изменяющийся от r o до r за время t.
При решении этого уравнения возможны несколько различных допущений. В первом приближении для квазистационарного процесса градиент концентрации 
может быть заменен отношением приращений 
. Тогда
.
Введя в данное выражение скорость из выражения (3.3)
,
получим
(3.6)
Отсюда следует, что линейная скорость обратно пропорциональна толщине оксидного слоя. Разделим переменные и проинтегрируем
.
Тогда
,
то есть толщина слоя продукта изменяется во времени по параболическому закону 
. Введя 
из уравнения (3.2), получим выражение
,
которое известно как уравнение Яндера.
Оно является приближенным для частиц сферической формы, так как связь толщины слоя с радиусом непрореагировавшей части частицы малого размера оказывается более сложной.
Более строгий учет сферической симметрии может быть выполнен следующим образом. Уравнение (3.5) перепишем в виде 
. Интегрируя в приближении независимости скорости диффузионного потока от x
,
получаем
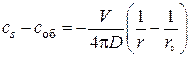или 
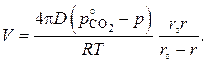(3.7)
Сопоставление уравнений (3.6) и (3.3) дает выражение для линейной скорости перемещения реакционной зоны
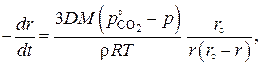(3.8)
которое указывает на более сложную, чем из (3.6), зависимость линейной скорости от размера r непрореагировавшей части карбоната. На начальном этапе, когда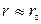 
и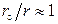 
сферическая симметрия частиц не проявляется, то есть линейная скорость, как и в предыдущем случае, обратно пропорциональна толщине оксидного слоя 
. Затем при 
с дальнейшим утолщением слоя продукта диссоциации (с уменьшением r) линейная скорость возрастает.
Интегрирование уравнения (3.8) и введение степени превращения 
через отношение (3.2) приводит к кинетическому уравнению
(3.9)
Приведенное к форме
оно известно как уравнение Кранка, Гистлинга и Браунштейна. Это уравнение оказывается более точным по сравнению с уравнением Яндера, так как было учтено изменение объема сферы по ходу реакции.
Из уравнения (3.9) время полного завершения диссоциации карбоната 
(3.10)
Сравнение с уравнением (3.4) для времени завершения процесса в кинетическом режиме приводит качественно к тем же выводам. Однако для процесса в диффузионном режиме следует отметить более сильное влияние размера зерен карбоната и менее сильное влияние температуры, так как к сильному уменьшению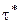 
за счет экспоненциального роста 
и 
с ростом температуры добавляется некоторое увеличение 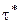с ростом величины T, находящейся в числителе уравнения (3.10).
Пример 3.1. В таблице представлены экспериментальные данные по кинетике разложения карбоната кальция:
| Время t, мин | |||||||
| P, атм | 1053 К | 0,025 | 0,034 | 0,044 | 0,055 | 0,065 | 0,073 |
| 1093 К | 0,025 | 0,058 | 0,083 | 0,114 | 0,136 | 0,164 | |
| 1123 К | 0,035 | 0,090 | 0,147 | 0,200 | 0,240 | 0,280 | |
| Время t, мин | |||||||
| P, атм | 1053 К | 0,080 | 0,085 | 0,088 | 0,092 | 0,094 | |
| 1093 К | 0,182 | 0,190 | |||||
| 1123 К | 0,310 | 0,340 | 0,355 |
Представить данные графически. Проанализировать. Вычислить константы скорости при температурах опыта и энергию активации процесса.
Решение. Приведенные в примере данные характеризуют опыты по разложению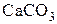 
в статических условиях в реакторе постоянного объема при постоянной температуре и нарастающим давлением (от вакуума до сравнительно небольших величин). Такие условия характерны для протекания процесса в кинетическом режиме. Представим данные опыта графически (рис. 3.2).
Видно, что в условиях опытов временная зависимость давления продукта имеет монотонный характер, и автокаталитический период отсутствует. Это может быть связано с наличием дисперсного карбоната и значительными для данного карбоната температурами.
Проверим применимость для описания кинетики процесса уравнения 
.
Скорость диссоциации можно оценить изменением давления образующегося газа в единицу времени и найти ее значения в различные моменты времени либо графическим дифференцированием, либо аналитически после выбора эмпирических формул, корректно описывающих кинетические кривые p – t.
На рис 3.2 кривые проведены с помощью одной из расчетно-графических программ ЭВМ и показаны уравнения линий и коэффициенты корреляции переменных. Эти уравнения позволяют найти производные 
и вычислить скорости разложения 
при температурах опытов. Например, из эмпирического уравнения временной зависимости
для 1053 К следует, что скорости разложения можно вычислять из уравнения
.
Результаты представлены графически в виде зависимостей скорости от времени и от 
(рис. 3.3 и 3.4). Значения равновесных давлений вычисляются из известного уравнения 
(см. пример 2.1). Они равны 0,117; 0,239 и 0,395 атм при температурах опытов 1053 К; 1093 К и 1123 К.
Линейное уменьшение скорости процесса со временем (см. рис. 3.3) соответствует допущению об отсутствии заметных диффузионных осложнений в ходе процесса.
Зависимости скорости от 
(см. рис. 3.4) являются линейными не во всем интервале давлений. При повышенных давлениях, а точнее, при малых отклонениях их от равновесных значений линейность не соблюдается. Можно также отметить, что представленные уравнения прямых рис. 3.4 в конечном счете не соответствуют кинетическому уравнению 
. Наблюдаемые зависимости отражают более сложные закономерности, в частности, зависимости скорости процесса от температуры.
|
|
| Рис. 3.4. Зависимость скорости разложения СaCO3от степени химического пересыщения при температурах опытов и уравнения линий опытов | Рис. 3.5. Зависимость скорости разложения СaCO3от температуры и уравнение прямой |
Действительно, влияние температуры должно проявляться не только в изменении константы 
, но и через величину 
, в которую входит упругость диссоциации карбоната, зависящая от температуры. Поэтому уравнение Аррениуса вида 
должно быть применено не к анализу температурной зависимости константы , но к анализу суммарной скорости процесса. Входящая в уравнение энергия активации E называется кажущейся. Для ее вычисления находим для температур опытов скорости, соответствующие определенному значению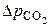 
, например, значению 0,1 атм, и строим график в координатах 
. Угловой коэффициент полученной линейной зависимости (рис. 3.5) соответствует кажущейся энергии активации 
.
Пример 3.2. В таблице представлены экспериментальные данные по кинетике разложения сульфида железа FeS2 (
– степень диссоциации сульфида). Представить данные графически. Проверить применимость к описанию кинетики данного процесса простых формально-кинетических уравнений связи степени превращения со временем. Сделать вывод о режиме протекания процесса. Вычислить энергию активации процесса.
| 873 К | t, мин | ||||||
 , %
| 21,1 | 31,6 | 42,8 | 49,6 | 69,0 | 86,3 | |
| 894 К | t, мин | ||||||
| , %
| 39,2 | 58,7 | 75,5 | 90,0 | 94,9 | ||
| 926 К | t, мин | ||||||
| , %
| 44,7 | 58,7 | 76,5 | 88,3 | 95,3 |
Решение. Графическое представление экспериментальных данных (рис. 3.6) не выявляет периода самоускорения процесса, и поэтому для анализа его возможно применение простых формально-кинетических уравнений, полученных для идеализированных условий протекания диссоциации в различных режимах. Проверим применимость кинетического уравнения Мак-Кевана 
и урав-нения Кранка, Гистлинга и Браунштейна
.
Введем обозначения функций этих уравнений:
; 
и вычислим их значения для указанных в опытах моментов времени. Результаты вычислений представим в табл. 3.1 и графически в координатах Y – t и Z – t (рис. 3.7 и 3.8).
Таблица 3.1
| 873 К | t, мин | ||||||
| Y | 0,076 | 0,119 | 0,17 | 0,204 | 0,323 | 0,485 | |
| Z | 0,0055 | 0,013 | 0,026 | 0,036 | 0,082 | 0,159 | |
| 894 К | t, мин | ||||||
| Y | 0,153 | 0,255 | 0,374 | 0,536 | 0,630 | ||
| Z | 0,021 | 0,054 | 0,105 | 0,185 | 0,230 | ||
| 926 К | t, мин | ||||||
| Y | 0,179 | 0,255 | 0,383 | 0,511 | 0,638 | ||
| Z | 0,028 | 0,054 | 0,109 | 0,172 | 0,234 |
| 
|
| Рис. 3.7. Кинетика разложения сульфида железа при различных температурах и уравнения линий | Рис. 3.8. Кинетика разложения сульфида железа при различных температурах (проверка линейности) |
Видно, что требуемая уравнениями линейность справедлива лишь для зависимостей Y – t. Следовательно, данные описываются уравнением Мак-Кевана.
На рис. 3.7 указаны уравнения прямых линий и коэффициенты корреляции переменных, мало отличающиеся от единицы. Так как уравнение Мак-Кевана соответствует протеканию процесса в кинетическом режиме, то следует сделать вывод, что диссоциация FeS2 протекает в условиях затрудненных химических превращений.
Для оценки влияния температуры на скорость процесса используем уравнение Аррениуса в виде . Для вычисления кажущейсяэнергии активации E строим график в координатах 
. Необходимые для этого данные представлены в табл. 3.2 и на рис. 3.9.
Угловой коэффициент полученной линейной зависимости (см. рис. 3.9) соответствует кажущейся энергии активации 
.
Рис. 3.9. Зависимость скорости разложения сульфида железа от температуры
| Таблица 3.2 | ||
| Константы уравнения Мак-Кевана | |||
| T, К | 1/ T | K | lg K |
| 0,001 15 | 0,001 67 | –2,777 | |
| 0,001 12 | 0,004 27 | –2,370 | |
| 0,001 08 | 0,008 61 | –2,065 | |