Кинетическая схема окисления металлов газами
Окисление металлов кислородсодержащими газами – процесс, обратный диссоциации оксидов. Термодинамические закономерности обоих процессов одни и те же. Наблюдается сходство и в кинетике данных процессов. Окисление металлов газами является процессом гетерогенным и, также как диссоциация, сопровождается превращением одних твердых фаз в другие. Продукт окисления выделяется в отдельную самостоятельную фазу, разделяющую металл и газ.
Процесс состоит из следующих стадий:
1. Внешняя диффузия газа-окислителя к наружной поверхности оксида.
2. Внутренняя реакционная диффузия реагентов в слое окалины.
3. Кристаллохимические превращения на границах раздела фаз.
Чаще всего наиболее медленной (лимитирующей) стадией является внутренняя диффузия. Поэтому скорость окисления металлов заметно зависит от сплошности, структуры и физико-химических свойств окалины. В общем случае окалина металлов переменной валентности состоит из нескольких оксидных слоев. Их расположение соответствует диаграммам состояния систем Me – O.
Сплошность окалины определяется соотношением мольных объемов оксида и металла. Если  , то образующийся оксидный слой пористый, и через него сравнительно легко идет диффузия окислителя к металлу. Окисление таких металлов (щелочных и щелочноземельных) идет до конца и с постоянной скоростью. Если
, то образующийся оксидный слой пористый, и через него сравнительно легко идет диффузия окислителя к металлу. Окисление таких металлов (щелочных и щелочноземельных) идет до конца и с постоянной скоростью. Если  , то образуется плотный слой окалины. Диффузия реагентов в оксидном слое затруднена, и при определенных условиях окалина может предохранять металл от дальнейшего окисления. Для таких металлов характерна двухсторонняя диффузия реагентов – кислорода и атомов (ионов) металла, причем для ряда металлов (Fe, Cu и др.) диффузия металла существенно выше диффузии кислорода. Структура, ее дефектность и свойства образующихся оксидов являются определяющими для механизма и кинетики реакционной диффузии при окислении этих металлов (Al, Cr, Ni, Mn, Fe и др.).
, то образуется плотный слой окалины. Диффузия реагентов в оксидном слое затруднена, и при определенных условиях окалина может предохранять металл от дальнейшего окисления. Для таких металлов характерна двухсторонняя диффузия реагентов – кислорода и атомов (ионов) металла, причем для ряда металлов (Fe, Cu и др.) диффузия металла существенно выше диффузии кислорода. Структура, ее дефектность и свойства образующихся оксидов являются определяющими для механизма и кинетики реакционной диффузии при окислении этих металлов (Al, Cr, Ni, Mn, Fe и др.).
Кинетические уравнения
Упражнение 4.1. На основе известных уравнений химической кинетики и стационарной диффузии получить выражение для скорости окисления металла. Проанализировать полученное кинетическое уравнение.
Принять следующие ограничения: а) процесс изобарно – изотермический; б) поверхность металла плоская; в) окалина состоит только из одного оксидного слоя; г) идет диффузия только кислорода; д) кристаллохимическое превращение соответствует реакции первого порядка; е) внешнедиффузионные торможения процесса отсутствуют.
Решение. Если скорости химической реакции и диффузии характеризовать изменением количеств веществ (моль) в единицу времени на единицу поверхности, то скорость реакции I порядка образования оксида на межфазной поверхности  .
.
 (моль
(моль  /м2∙с),
/м2∙с),
а скорость диффузии кислорода в соответствии с первым законом Фика
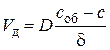 .
.
Здесь k –константа скорости кристаллохимического превращения (реакции); D – коэффициент диффузии кислорода в оксидном слое толщиной δ; с и с об – концентрации кислорода на межфазной поверхности  и на наружной поверхности оксида (в объеме газа).
и на наружной поверхности оксида (в объеме газа).
В стационарном состоянии указанные скорости равны. Это позволяет исключить неизвестную концентрацию с на межфазной поверхности.
 и
и 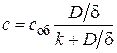 .
.
Тогда скорость окисления
 (4.1)
(4.1)
Анализ полученного выражения можно сделать, рассмотрев два крайних случая.
В случае тонкой пленки ( ) скорость диффузии кислорода велика,
) скорость диффузии кислорода велика, 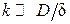 , и, пренебрегая значением К в знаменателе, получим выражение для скорости окисления в кинетическом режиме
, и, пренебрегая значением К в знаменателе, получим выражение для скорости окисления в кинетическом режиме  . Видно, что в тонких пленках (в начале процесса) скорость не зависит от толщины пленки.
. Видно, что в тонких пленках (в начале процесса) скорость не зависит от толщины пленки.
При больших значениях δив случае плотного слоя оксида  . Пренебрегая значением
. Пренебрегая значением  в знаменателе уравнения (4.1), получим выражение для скорости окисления в диффузионном режиме
в знаменателе уравнения (4.1), получим выражение для скорости окисления в диффузионном режиме  , из которого следует, что скорость окисления обратно пропорциональна толщине слоя.
, из которого следует, что скорость окисления обратно пропорциональна толщине слоя.
Таким образом, в зависимости от толщины пленки оксида (времени окисления) и свойств пленки возможен различный режим процесса и смена режима. Поэтому удобен временной анализ процесса по изменению толщины окалины или ее массы.
Упражнение 4.2. Изменив в упражнении 4.1 ограничение «г) идет диффузия только кислорода» на допущение «г) идет диффузия только металла», основанное на том, что диффузия частиц металла в оксидном слое идет намного быстрее диффузии кислорода, получить выражение для скорости окисления металла.
Решение. В данном случае рассматриваем гетерогенную реакцию окисления металла на внешней поверхности окалины (оксид–газ).
Скорость ее (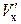 , моль
, моль  /м2∙с) равна
/м2∙с) равна
 ,
,
где  – константа скорости реакции;
– константа скорости реакции; 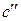 – концентрация металла на реакционной поверхности
– концентрация металла на реакционной поверхности  –газ.
–газ.
Скорость диффузии частиц металла к данной поверхности
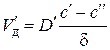 ,
,
где  – коэффициент диффузии металла в оксидном слое толщиной δ;
– коэффициент диффузии металла в оксидном слое толщиной δ; 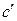 – концентрация металла на реакционной поверхности
– концентрация металла на реакционной поверхности  .
.
Из равенства скоростей 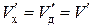 находим неизвестную концентрацию металла
находим неизвестную концентрацию металла 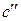 на реакционной поверхности
на реакционной поверхности  – газ
– газ

и скорость окисления
 (4.2)
(4.2)
Полученное выражение по форме совпадает с уравнением (4.1), хотя и содержит другие характеристики процесса. Поэтому анализ уравнения (4.2) аналогичен ранее выполненному для выражения (4.1).
Упражнение 4.3. Выразив скорость окисления металла через изменение толщины окалины, преобразовать кинетическое уравнение (4.1) и получить зависимость толщины окалины от времени. Проанализировать полученное выражение.
Решение. Связь молярной скорости V [моль  /(м2∙с)] с линейной
/(м2∙с)] с линейной  [м/(м2∙с)] может быть записана в виде
[м/(м2∙с)] может быть записана в виде
 (4.3)
(4.3)
Подставляя (4.3) в (4.1), получим дифференциальное уравнение для линейной скорости
 .
.
Здесь  – молярный объем оксида;
– молярный объем оксида;  и М – его плотность и молярная масса; s – площадь реакционной поверхности.
и М – его плотность и молярная масса; s – площадь реакционной поверхности.
После интегрирования зависимость толщины окалины от времени имеет вид
 .
.
Видно, что при малых значениях  , когда можно пренебречь первым слагаемым, выполняется линейная зависимость толщины слоя от времени
, когда можно пренебречь первым слагаемым, выполняется линейная зависимость толщины слоя от времени  , и процесс определяется константой скорости реакции (кинетический режим).
, и процесс определяется константой скорости реакции (кинетический режим).
Для толстых и плотных слоев, когда  и можно пренебречь вторым слагаемым, становится справедливой параболическая зависимость толщины слоя от времени
и можно пренебречь вторым слагаемым, становится справедливой параболическая зависимость толщины слоя от времени
 .
.
Можно отметить аналогичные зависимости толщины слоя от парциального давления кислорода в газовой фазе, так как  .
.
Упражнение 4.4. На основе уравнения (4.2) в упражнении 4.2, выразив скорость окисления металла через изменение массы окалины, получить зависимости массы окалины от времени и прироста массы окисляемого металла от времени для диффузионного режима коррозии.
Решение. Учитывая, что для диффузионного режима  , запишем уравнение (4.2) в виде
, запишем уравнение (4.2) в виде  . Выразим скорость через массу металла
. Выразим скорость через массу металла  , перешедшего в оксид
, перешедшего в оксид  , а концентрацию металла на реакционной поверхности
, а концентрацию металла на реакционной поверхности 
 через плотность металла
через плотность металла 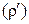
 ,
,  .
.
Тогда
 .
.
Толщину слоя окалины выразим через массу оксида 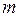 и его плотность ρ
и его плотность ρ
 ,
,
а массу оксида  через массу окисленного металла
через массу окисленного металла  . После преобразований данных выражений получим
. После преобразований данных выражений получим
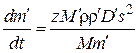 или
или  .
.
После интегрирования имеем
 (4.4)
(4.4)
Удобно характеризовать кинетику окисления металлов, измеряя прирост массы окисляющегося металла
 .
.
Отсюда  . Подставив последнее выражение в уравнение параболы (4.4), получим
. Подставив последнее выражение в уравнение параболы (4.4), получим
 , (4.5)
, (4.5)
где  представляет коэффициент природы и свойств металла и его оксида, включающий площадь внешней поверхности
представляет коэффициент природы и свойств металла и его оксида, включающий площадь внешней поверхности  .
.
Таким образом, увеличение со временем массы металла, окисляемого в диффузионном режиме при постоянной температуре, соответствует параболическому закону.
Пример 4.1. Установить математическую зависимость для кинетического закона окисления кальция на воздухе при 773 К на основе следующих экспериментальных данных по привесу образца металла ∆ m со временем t.
| t, ч | ||||||||
| ∆ m, г/м2 |
 Решение. По опытным данным с помощью ЭВМ строим график в координатах ∆ m – t. Он представляет линейную зависимость прироста массы от времени. Уравнение данной зависимости и коэффициент корреляции указаны в области построения графика. Полученное уравнение прямой с высокой степенью достоверности подтверждает постоянство скорости окисления кальция как представителя металлов, оксиды которых не образуют сплошных пленок на поверхности. Скорость окисления Са при 773 К равна
Решение. По опытным данным с помощью ЭВМ строим график в координатах ∆ m – t. Он представляет линейную зависимость прироста массы от времени. Уравнение данной зависимости и коэффициент корреляции указаны в области построения графика. Полученное уравнение прямой с высокой степенью достоверности подтверждает постоянство скорости окисления кальция как представителя металлов, оксиды которых не образуют сплошных пленок на поверхности. Скорость окисления Са при 773 К равна

 г/м2∙ч.
г/м2∙ч.
Пример 4.2. Установить математическую зависимость для кинетического закона окисления бериллия на воздухе при 673 К на основе следующих экспериментальных данных по привесу образца металла ∆ m со временем t.
| t, ч | |||||
| ∆ m, мг/cм2 | 12,78 | 40,18 | 100,45 | 126,02 |
Решение. По опытным данным с помощью ЭВМ строим график в координатах ∆ m – t (рис. 4.2). Он представляет нелинейную зависимость прироста массы от времени. Проверяем, подбирая в качестве аппроксимирующей зависимости степенную функцию, не является ли искомая зависимость параболической. Действительно, обработка данных с помощью ЭВМ приводит к уравнению квадратной параболы, представленному на рис. 4.2. Дополнительным подтверждением установленной зависимости является показанная на рис 4.3 линейность связи  и
и  . Линейность соответствует теоретическому уравнению
. Линейность соответствует теоретическому уравнению  (4.5), представленному в виде
(4.5), представленному в виде  . Угловой коэффициент (0,5) в данном уравнении согласуется с небольшим отклонением (с коэффициентом 0,502) в уравнении, приведенном на рис. 4.3.
. Угловой коэффициент (0,5) в данном уравнении согласуется с небольшим отклонением (с коэффициентом 0,502) в уравнении, приведенном на рис. 4.3.

| 
|
| Рис. 4.2. Кинетика окисления Ве при 673 К | Рис. 4.3. Подтверждение параболической зависимости |
Таким образом, окисление бериллия на воздухе при 673 К может быть описано кинетическим уравнением параболы 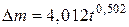 (мг/cм2), где t – время в час.
(мг/cм2), где t – время в час.
Пример 4.3. На основе опытных данных по кинетике окисления меди на воздухе установить закон роста оксидного слоя и температурную зависимость константы скорости или коэффициента диффузии процесса окисления. Найти энергию активации процесса. Площадь поверхности пластины меди  .
.
| 993 К |  , с , с
| |||||||||
 , мг , мг
| 2,5 | 7,5 | 8,5 | 9,5 | ||||||
| 1083 К |  , с , с
| |||||||||
 , мг , мг
| 2,5 | 3,5 | 4,5 | 5,5 | ||||||
| 1143 К |  , с , с
| |||||||||
 , мг , мг
|
Решение (вариант 1). По опытным данным с помощью ЭВМ строим график в координатах ∆ m – t (рис. 4.4). Он представляет нелинейную зависимость прироста массы от времени. В качестве аппроксимирующей зависимости выбираем степенную функцию. Как видно представленные на рис. 4.4 параболы с достаточной степенью достоверности  описывают опытные данные.
описывают опытные данные.
Подтверждением этому служит линейный характер зависимостей  от
от  , представленных на рис. 4.5 при температурах опытов серией параллельных прямых с угловым коэффициентом
, представленных на рис. 4.5 при температурах опытов серией параллельных прямых с угловым коэффициентом  . Таким образом, окисление меди на воздухе при всех температурах опытов может быть описано кинетическим уравнением параболы
. Таким образом, окисление меди на воздухе при всех температурах опытов может быть описано кинетическим уравнением параболы  , или
, или  . Это уравнение обращается в уравнение прямой в логарифмических координатах.
. Это уравнение обращается в уравнение прямой в логарифмических координатах.

| 
|
| Рис. 4.4. Кинетика окисления меди на воздухе: 1 –993 К; 2 –1083 К; 3 –1143 К | Рис. 4.5. Проверка параболической зависимости 1 –993 К; 2 –1083 К; 3 –1143 К |
В соответствии с полученными в упражнении 4.4 теоретическими уравнениями следует считать, что окисление меди проходило при условиях диффузионного режима, а коэффициент В в уравнении параболы равен:
 .
.
Подставляя в данное выражение справочные значения плотности  и
и  , равные
, равные  = 6,1 г/см3 и
= 6,1 г/см3 и  = 8,93 г/см3, а также молярных масс меди
= 8,93 г/см3, а также молярных масс меди  = 63,54 г/моль; оксида меди
= 63,54 г/моль; оксида меди 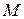 = 143,08 г/моль; стехиометрического коэффициента в формуле
= 143,08 г/моль; стехиометрического коэффициента в формуле 
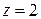 и площади поверхности пластин меди
и площади поверхности пластин меди 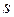 = 4,5 см2, получим
= 4,5 см2, получим 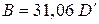 г2/см2 =
г2/см2 =  мг2/см2.
мг2/см2.
После логарифмирования уравнения параболы  получим выражение
получим выражение  . Принимая его идентичным (с небольшой погрешностью) с уравнениями, представленными на рис. 4.5, можно из сравнения свободных слагаемых в уравнениях прямых найти коэффициент диффузии меди в оксиде
. Принимая его идентичным (с небольшой погрешностью) с уравнениями, представленными на рис. 4.5, можно из сравнения свободных слагаемых в уравнениях прямых найти коэффициент диффузии меди в оксиде  при температурах опытов.
при температурах опытов.
 Например, из уравнения прямой
Например, из уравнения прямой  для опыта при 993 К следует
для опыта при 993 К следует 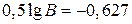 или
или  . Отсюда
. Отсюда  и
и 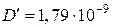 см2/с. Вычисления для опытов при других температурах дают следующие значения коэффициентов диффузии меди:
см2/с. Вычисления для опытов при других температурах дают следующие значения коэффициентов диффузии меди:  см2/с (810 °С) и
см2/с (810 °С) и  см2/с (1143 К).
см2/с (1143 К).
Полученные значения  позволяют определить энергию активации процесса диффузии меди в оксиде
позволяют определить энергию активации процесса диффузии меди в оксиде  (E) на основании известной зависимости
(E) на основании известной зависимости 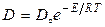 , где
, где 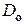 – предэкспоненциальный множитель. Для этого температурную зависимость коэффициента диффузии записываем в виде
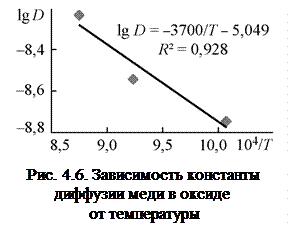
– предэкспоненциальный множитель. Для этого температурную зависимость коэффициента диффузии записываем в виде  и строим график в координатах
и строим график в координатах  и
и  (рис. 4.6). Из равенства
(рис. 4.6). Из равенства  находим
находим  кДж/моль.
кДж/моль.
 Решение (вариант 2). По опытным данным с помощью ЭВМ строим график в координатах
Решение (вариант 2). По опытным данным с помощью ЭВМ строим график в координатах  – t (рис. 4.7). Он представляет нелинейную зависимость прироста массы от времени. В соответствии с теоретическими положениями в качестве аппроксимирующей зависимости выбираем степенную функцию (квадратичную параболу). Для подтверждения ее применимости к описанию опытных данных строим график в координатах
– t (рис. 4.7). Он представляет нелинейную зависимость прироста массы от времени. В соответствии с теоретическими положениями в качестве аппроксимирующей зависимости выбираем степенную функцию (квадратичную параболу). Для подтверждения ее применимости к описанию опытных данных строим график в координатах  – t (рис. 4.8). Видно, что требуемая уравнением параболы
– t (рис. 4.8). Видно, что требуемая уравнением параболы  линейность в данных координатах выполняется.
линейность в данных координатах выполняется.
Приведенные на рис. 4.8 значения коэффициентов B (0,053; 0,090; 0,174) позволяют из выражения  найти константы диффузии меди
найти константы диффузии меди  в оксиде
в оксиде  при температурах опытов. Вычисленные коэффициенты диффузии равны:
при температурах опытов. Вычисленные коэффициенты диффузии равны:

| |||
 , см2/с , см2/с
| 1,71·10–9 | 2,90·10–9 | 5,60·10–9 |

| 
|
| Рис. 4.8. Проверка параболической зависимости при 1 –993 К; 2 –1083 К; 3 –1143 К | Рис. 4.9. Зависимость константы диффузии меди в оксиде от температуры |
С помощью известной зависимости  , находим энергию активации E процесса диффузии меди в оксиде
, находим энергию активации E процесса диффузии меди в оксиде 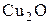 . Для этого температурную зависимость коэффициента диффузии записываем в виде
. Для этого температурную зависимость коэффициента диффузии записываем в виде 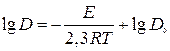 и строим график в координатах
и строим график в координатах  и
и  (рис. 4.9).
(рис. 4.9).
Из равенства  (см. рис. 4.9) вычисляем
(см. рис. 4.9) вычисляем  кДж.
кДж.
Вывод. Таким образом, обработка данных эксперимента показала, что процесс окисления меди на воздухе в интервале температур 983–1143 К протекает в диффузионном режиме. Установлен параболический закон окисления меди  . Найдена температурная зависимость коэффициента диффузии меди в оксиде
. Найдена температурная зависимость коэффициента диффузии меди в оксиде 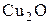 в виде
в виде  (cм2/с)
(cм2/с)  . Энергия активации коррозии меди равна 72,2 кДж.
. Энергия активации коррозии меди равна 72,2 кДж.