Равномерное и равнопеременное вращение.

Коллоквиум по физике.

№1
Система отсчета. Основные кинематические характеристики поступательного движения: радиус-вектор, перемещение, путь, скорость, ускорение. Кинематика поступательного движения: равномерное и равнопеременное движение.

Ответ:

Механика — часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движе­ние — это изменение с течением времени взаимного расположения тел или их частей. Механика делится на три раздела: I) кинематику; 2) динамику; 3) статику.

Кинематика изучает движение тел, не рассматривая причины, которые это движение обусловливают.

Поступательное движение — это движение, при кото­ром любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение — это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Система отсчета — совокупность системы координат и часов, связанных с телом от­счета. В декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y и z или радиусом-вектором r, проведенным из начала системы координат в данную точку.

При движении материальной точки ее координаты с течением времени изменяются. В общем случае ее движение определяется скалярными уравнениями

x = x(t), у = y(t), z = z(t) эквивалентными векторному уравнению r = r (t). Эти уравнения называются кинематическими уравнениями дви­жения материальной точки.
Перемещение - вектор D r = r — r ₀, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиуса-вектора точки за рассматриваемый промежуток времени.

Радиус - вектор (для произвольной точки в пространстве) — это вектор, идущий из начала координат в эту точку.

Скорость

Скорость – векторная величина которой определяется как быстрота движения, так и его направ­ление в данный момент времени.
Мгновенная скорость – при неог­раниченном уменьшении D t средняя скорость стремится к предельному значению. которое называется мгновенной скоростью v:

Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пре­деле совпадает с касательной, то вектор скорости v направлен по касательной к траек­тории в сторону движения (рис. 3). По мере уменьшения D t путь D s все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости: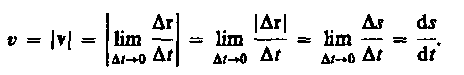
При неравномерном движении — модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной á v ñ — средней скоро­стью неравномерного движения: 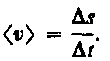(формула 2.2)

Вектором средней скорости <v> называется отношение приращения Dr радиу­са-вектора точки к промежутку времени D t: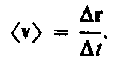

Путь — длина участка траектории материальной точки, пройденного точкой за определенное время.
Длина пути - длина участка траектории АВ, пройденного материальной точкой с момента начала отсчета времени D s и является скалярной функцией времени: D s = D s(t). (рис.2)

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |D r | равен пройденному пути D s.

Если выражение d s = v d t (см. формулу (2.2)) проинтегрировать по времени в пре­делах от t до t + D t, то найдем длину пути, пройденного точкой за время D t: (2.3)
При равномерном движении(2.3) имеет вид: Длина пути, пройденного точкой за промежуток времени от t ₁ до t _2: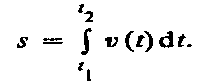

Ускорение

Ускорение - физическая величина, характеризующая быстроту изменения скорости по модулю и направлению.
Средним ускорением неравномерного движения в интервале от t до t + D t называется векторная величина, равная отношению изменения скорости Dv к интервалу вре­мени D t
Мгновенное ускорение– предел среднего ускорения: т.е.:

Ускорение a - векторная величина, равная первой производной скорости по времени.

Равномерное и равнопеременное движения:

В зависимости от тангенциальной и нормальной составляющих ускорения движе­ние можно классифицировать следующим образом:

1) 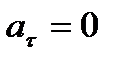, а_n = 0 — прямолинейное равномерное движение;

2) , а_n = 0 — прямолинейное равнопеременное движение. 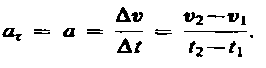Если начальный момент времени t ₁=0, а начальная скорость v ₁ =v ₀, то, обозначив t ₂ =t и v ₂ =v, получим 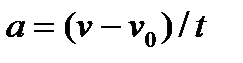, откуда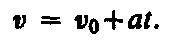

Длина пути, пройденного точкой, в случае равнопеременного движения: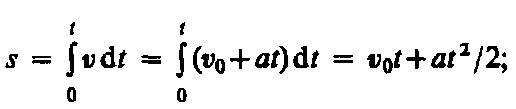
3) 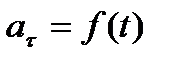, а_n = 0— прямолинейное движение с переменным ускорением;

4) , а_n = const. При скорость по модулю не изменяется, а изменяется по направлению. Из формулы a_n=v ² /r следует, что радиус кривизны должен быть посто­янным. Следовательно, движение по окружности является равномерным;

5) , — равномерное криволинейное движение;

6) 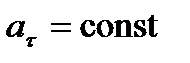, — криволинейное равнопеременное движение;

7) 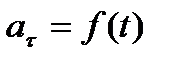, — криволинейное движение с переменным ускорением.

№2
Основные кинематические характеристики вращательного движения: угловой путь, угловая скорость, угловое ускорение. Соотношения между кинематическими характеристиками поступательного и вращательного движения. Равномерное и равнопеременное вращение.

Угловой путь 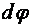– скалярная величина, равная углу, на который перевернется радиус-вектор 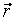данной точки за время dt

Угловая скорость - векторная величина, равная первой производной угла поворота тела по времени: .
Линейная скорость точки т.е.
Формула для линейной скорости в векторном виде: При этом модуль векторного произведения, по определению, равен 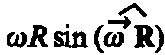, а направление совпадает с направлением поступательного движения правого винта при его вращении от к R.
Если ( = const, то вращение равномерное и его можно характеризовать периодом вращения T — временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени D t = T соответствует 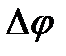= 2p, то = 2p/ T, откуда 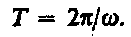. Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения: 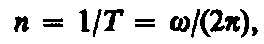откуда

Угловое ускорение - векторная величина, равная первой производной угловой скорости по времени: 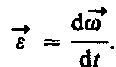При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор сонаправлен вектору (рис.8), при замедлен­ном — противонаправлен ему.

Соотношения между кинематическими характеристиками поступательного и вращательного движения:

Между поступательным и вращательным движениями существует аналогия, которая позволяет легко запоминать формулы, относящиеся к вращательному движению.
Основные характеристики поступательного движения: путь S, скорость v, ускорение а и время t. При вращении им соответствуют: угол поворота φ, угловая скорость со, угловое ускорение ε и время t.

Равномерное и равнопеременное вращение.

Равномерное вращение - вращение тела с постоянной угловой скоростью ω = const.
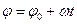. (3.7) - уравнение равномерного вращения тела.
Из уравнения (3.7) находим , то есть угловая скорость равномерного вращения тела равна отношению приращения угла поворота за некоторый промежуток времени к величине этого промежутка времени.
Равнопеременное вращение - вращение тела при котором угловое ускорение постоянно (ε=const) во все время движения.
З акон равнопеременного вращения, если при t= 0, φ=φ₀, ω=ω₀. соответствующих: , или

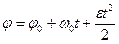
№3

Тангенциальное и нормальное ускорения. Ускорение при криволинейном движении.
Ответ:

Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
Тангенциальная составляющая ускорения: 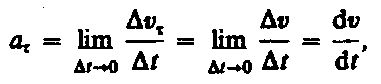т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
Нормальная составляющая ускорения: 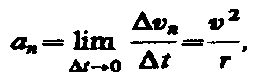направлена по нормали к траектории к центру ее кривизны (поэтому ее называют также центростремительным ускорением).
Полное ускорение тела - геометрическая сумма тангенциальной и нормальной составляющих: 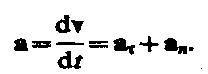.Итак, тангенциальная составляющая ускорения характеризует быстроту изменения скорости по модулю (направлена по касательной к траектории), а нормальная состав­ляющая ускорения — быстроту изменения скорости по направлению (направлена к цен­тру кривизны траектории).

№4
Понятие силы и массы. Инерциальные системы отсчета. Законы Ньютона в механике.

Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные и гравитационные свойства.
Сила — это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.
Инерциальная система отсчета – только в этой системе отсчета выполняется Первый Закон Ньютона. Инерциальной системой отсчета является такая система отсчета, относительно которой материальная точка, свободная от внешних воздействий, либо покоится, либо движется равномерно и прямолинейно. Первый закон Ньютона утверждает существование инерциальных систем отсчета. Пример: Гелиоцентрическая (звездную) система.

Законы Ньютона.

Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние. Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют также законом инерции.
Второй Закон Ньютона: в инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки. Формула:

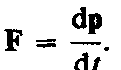(или уравнение движения материальной точки)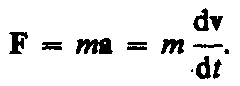

Третий Закон Ньютона: материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению. F₁₂ = – F₂₁,

F₁₂ — сила, действующая на первую материальную точку со стороны второй;

F₂₁ — сила, действующая на вторую материальную точку со стороны первой.

№5