Динамические характеристики вращательного движения (момент силы, момент импульса, момент инерции).

Моментом инерции системы (тела) - относительно данной оси называется физическая величина, равная сумме произведений масс и материальных точек системы на квадраты их расстояний до рассматриваемой оси:
В случае непрерывного распределения масс:
Момент инерции сплошного цилиндра:
Теорема Штейнера: : момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями.

Кинетическая энергия вращающегося тела: 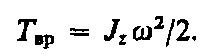где J_z — момент инерции тела относительно оси z.
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r, проведенного из точ­ки О в точку А приложения силы, на силу F: , где a— угол между r и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.
Моментом силы относительно неподвижной оси z называется скалярная величина M_z, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (рис. 26). Значение момента М_z не зависит от выбора положения точки О на оси z.

Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:
Уравнение динамики вращательного движения твердого тела относительно неподвижной оси: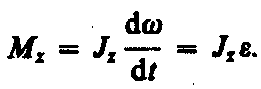
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произ­ведением:

Модуль вектора момента импульса: , где

L — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р, где a — угол между векторами r и р, l — плечо вектора р относительно точки О.

 

Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.

Момент импульса отдель­ной частицы:
З акон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

 

№11
Уравнение динамики вращательного движения (без вывода).

Уравнения динамики вращательного движения твер­дого тела:

т. е.

№12
Момент импульса. Закон сохранения момента импульса (без вывода).

Момент импульса:
З акон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.

№13
Сравнительные характеристики поступательного и вращательного движений.

Основные характеристики поступательного движения: путь S, скорость v, ускорение а и время t. При вращении им соответствуют: угол поворота φ, угловая скорость со, угловое ускорение ε и время t.
Пусть нам нужно написать уравнение равномерного вращательного движения. Вспоминаем формулу S=vt, справедливую для равномерного поступательного движения, и по аналогии пишем уравнение равномерного вращательного движения: φ=ωt. Для равномерного ускоренного (или замедленного) вращения справедливы формулы: угол поворота φ= ω₀t±at²/2 и угловая скорость ω=ω₀±εt (по аналогии с S=v₀t±at²/2 и v=v₀±at). В этих формулах знак "плюс" относится к случаю равномерно ускоренного движения, знак "минус" - равномерно замедленного.

№14
Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Силовые линии электростатического поля. Напряженность поля точечного заряда.

Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Закон сохранения электрического заряда q₁ + q₂ + q₃ +... + q_n = const где q₁, q₂ и т.д. – заряды частиц.
Напряженность поля точечного заряда -
Зако́н Куло́на — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами. Формулировка: Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом: или - закон Кулона в векторной форме, где — сила, с которой заряд 1 действует на заряд 2; 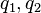— величина зарядов; — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — ); — коэффициент пропорциональности.

Где E — напряженность электрического поля (Вольт/метр), F — сила действующая на заряд Q (Ньютон), Q — заряд (Кулон)

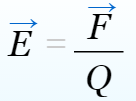Напряженность электрического поля — это отношение силы, действующей на заряд, к величине заряда. ггг

При́нцип суперпози́ции - Результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Силовые линии электростатического поля имеют следующие свойства:
-- Всегда незамкнуты: начинаются на положительных зарядах (или на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности).
-- Не пересекаются и не касаются друг друга.
-- Густота линий тем больше, чем больше напряжённость, то есть напряжённость поля прямо пропорциональна количеству силовых линий, проходящих через площадку единичной площади, расположенную перпендикулярно линиям.

№15
Работа в электрическом поле. Потенциальная энергия. Потенциал электрического поля. Потенциал поля точечного заряда. Эквипотенциальные поверхности. Связь напряженности и потенциала.

Работа в электрическом поле:
Потенциальная энергия — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся вполне консервативных сил.

E р = mgh

Электростатический потенциа́л — скалярная энергетическая характеристикаэлектростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля
Потенциал поля точечного заряда:
Эквипотенциальная поверхность — воображаемая поверхность, все точки которой имеют одинаковый потенциал.
Связь напряженности и потенциала:

№16
Поток вектора напряженности электрического поля. Теорема Гаусса в вакууме.

Теорема Гаусса в вакууме:
Поток вектора напряженности электрического поля

где E_n – произведение вектора на нормаль к данной площадке

№17
Применение теоремы Гаусса для расчета электрических полей и потенциалов заряженных тел: плоскость, две плоскости, полая сфера (без вывода).

Плоскость:
Две плоскости:
Полая сфера:

№18
Проводники в электрическом поле. Напряженность электрического поля у поверхности проводника. Электростатическая индукция. Электростатическая защита.

 

Проводники — тела, в которых электрический заряд может перемещаться по всему его объему. Проводники делятся на две группы: 1) про­водники первого рода (металлы) — перенос в них зарядов (свободных электронов) не сопровождается химическими превращениями; 2) проводники второго рода (например, расплавленные соли, растворы кислот) — перенос в них зарядов (положительных и отрицательных ионов) ведет к химическим изменениям.

 

Напряженность поля равномерно заряженной сферической поверхности в точках, лежащих вне и внутри сферы на расстоянии r от ее центра, соответственно равна:

Электростатическая индукция — явление наведения собственного электростатического поля, при действии на тело внешнего электрического поля.
Электростатическая защита — помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля.

 

№19

Электрическая емкость уединенного проводника. Конденсаторы. Расчет электроемкости для: плоского конденсатора. Параллельное и последовательное соединение конденсаторов (формулы).

 

Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: , где e - диэлектрическая проницаемость окружающей среды. Следовательно:

Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Емкость плоского конденсатора.

, т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости.
Параллельное соединение конденсаторов

На рис. 1 изображено параллельное соединение нескольких конденсаторов. В этом случае напряжения, подводимые к отдельным конденсаторам, одинаковы: U1 = U2 = U3 = U. Заряды на обкладках отдельных конденсаторов: Q1 = C1U, Q2 = C2U, Q3 = C3U, а заряд, полученный от источника Q = Q1 + Q2 + Q3.

Рис. 1. Схема параллельного соединения конденсаторов

Общая емкость равнозначного (эквивалентного) конденсатора:

C = Q / U = (Q1 + Q2 + Q3) / U = C1 + C2 + C3,

т. е. при параллельном соединении конденсаторов общая емкость равна сумме емкостей отдельных конденсаторов.