Последовательное соединение конденсаторов

При последовательном соединении конденсаторов (рис. 3) на обкладках отдельных конденсаторов электрические заряды по величине равны: Q1 = Q2 = Q3 = Q

Действительно, от источника питания заряды поступают лишь на внешние обкладки цепи конденсаторов, а на соединенных между собой внутренних обкладках смежных конденсаторов происходит лишь перенос такого же по величине заряда с одной обкладки на другую (наблюдается электростатическая индукция), поэтому и на них по- являются равные и разноименые электрические заряды.

Рис. 3. Схема последовательного соединения конденсаторов

Напряжения между обкладками отдельных конденсаторов при их последовательном соединении зависят от емкостей отдельных конденсаторов: U1 = Q/C1, U1 = Q/C2, U1 = Q/C3, а общее напряжение U = U1 + U2 + U3

Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.

Формулы эквивалентных емкостей аналогичны формулам эквивалентных проводимостей.

№20
Энергия системы зарядов, уединенного проводника и конденсатора. Плотность энергии электростатического поля (формулы).

Энергия системы неподвижных точечных зарядов.

где j ₁₂ и j ₂₁ — соответственно потенциалы, создаваемые зарядом Q ₂ в точке нахожде­ния заряда Q ₁ и зарядом Q ₁ в точке нахождения заряда Q ₂. Согласно (84.5),

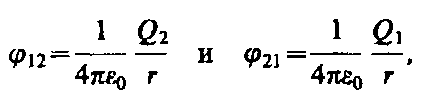поэтому W ₁ = W ₂ = W и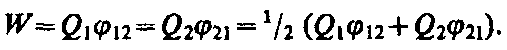

Добавляя к системе из двух зарядов последовательно заряды Q ₃, Q ₄ ,..., можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

Энергия заряженного уединенного проводника. Пусть имеется уединенный провод­ник, заряд, емкость и потенциал которого соответственно равны Q, С, j. Увеличим заряд этого проводника на d Q. Для этого необходимо перенести заряд d Q из бесконеч­ности на уединенный проводник, затратив на это работу, равную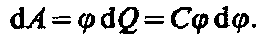
Чтобы зарядить тело от нулевого потенциала до j, необходимо совершить работу

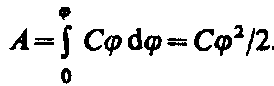(95.2). Энергия заряженного проводника равна той работе, которую необходимо совер­шить, чтобы зарядить этот проводник: 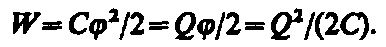(95.3)

Формулу (95.3) можно получить и из того, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Пола­гая потенциал проводника равным j, из (95.1) найдем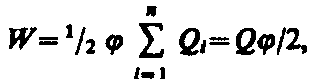
где 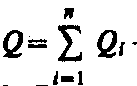- заряд проводника.

Энергия заряженного конденсатора. Как всякий заряженный проводник, конден­сатор обладает энергией, которая в соответствии с формулой (95.3) равна
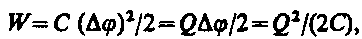(95.4)где Q — заряд конденсатора, С — его емкость, Dj — разность потенциалов между обкладками конденсатора.

Используя выражение (95.4), можно найти механическую (пондеромоторную) силу, с которой пластины конденсатора притягивают друг друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину d x. Тогда действующая сила совершает работу d A=F d x вследствие уменьшения потенциальной энергии системы F d x = — d W, откуда (95.5)Подставив в (95.4) выражение (94.3), получим

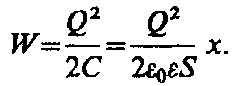(95.6)Производя дифференцирование при конкретном значении энергии (см. (95.5) и (95.6)), найдем искомую силу: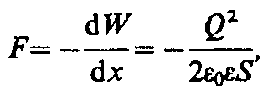

где знак минус указывает, что сила F является силой притяжения.

Плотность энергии электрического поля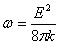
Объемная плотность энергии электростатического поля (энергия единицы объема)

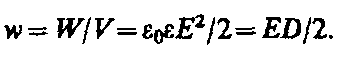
№21
Постоянный электрический ток: плотность тока, сила тока.

Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов.
Сила тока I скалярная физи­ческая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени: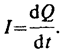
Для постоянного тока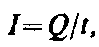
Физическая величина, определяемая силой тока, проходящего через единицу площа­ди поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:

№22
Сторонние силы. ЭДС и напряжение.

Сторонние силы - это силы неэлектростатического происхождения, действующие на заряды со стороны источников тока.

Сторонние силы совершают работу по перемещению электрических зарядов. Физи­ческая величина, определяемая работой, совершаемой сторонними силами при переме­щении единичного положительного заряда, называется электродвижущей силой (э.д.с.), действующей в цепи: 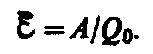э. д. с., действующей в цепи: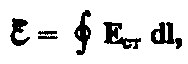
Э.д.с., действующая на участке 1 — 2, равна

Напряжение U на участке 1 — 2 - физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторон­них сил при перемещении единичного положительного заряда на данном участке цепи.

№23
Закон Ома для однородного участка цепи в интегральной и дифференциальной формах. Сопротивление проводника, зависимость его от температуры. Сопротивление при параллельном и последовательном соединении проводников (формулы). Электропроводность проводников.

Закон Ома:
Закон Ома в дифференциальной форме 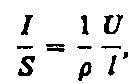где r — коэффициент пропорциональности l-длина.
Закон Ома в интегральной форме: 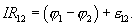и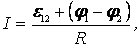
Удельное сопротивление: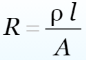
Температурная зависимость сопротивления: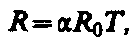
Сопротивление проводников при параллельном соединении: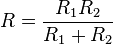
Сопротивление проводников при последовательном соединении:

Электропроводностью проводника называют величину (1 / R), обратную сопротивлению.

№24
Работа и мощность тока. Закон Джоуля-Ленца в интегральной и дифференциальной формах.

Работа тока Если сопротивление проводника R, то, используя законОма, получим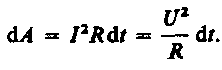
Мощность тока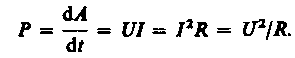
Закон Джоуля-Ленца в интегральной форме: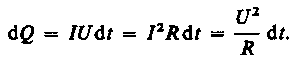
Закон Джоуля-Ленца в дифференциальной форме: 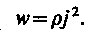и

№25
Закон Ома для неоднородного участка цепи, для замкнутой цепи.

Закон Ома для неоднородного участка цепи в интегральной форме, который является обобщенным законом Ома.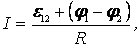
Закон Ома для замкнутой цепи: