1. Коэффициент корреляции знаков (коэффициент Фехнера)основан на сопоставлении знаков отклонений от средней величины и подсчете числа случаев совпадения и несовпадения знаков.
 (7.13)
(7.13)
где i – коэффициент корреляции знаков;
U – число пар с одинаковыми знаками отклонений X и Y от средних значений;
V – число пар с разными знаками отклонений X и Y от средних значений.
Этот показатель изменяется от –1 до +1.
Если i<0, то имеет место обратная зависимость; i>0 – прямая зависимость; i=0 – связи нет; i=±1 – связь функциональная, а не корреляционная.
Пример расчета коэффициента корреляции знаков.
Имеются следующие данные по 10 фирмам, реализующим турпутевки.
Таблица 7.4 – Реализация путевок и стоимость основных фондов в турфирмах района
| № фирмы | Стоимость ОФ, млн. руб. Х | Реализация путевок, млн. руб. Y | Знак отклонения от ср. арифм. | Ранг | Разность рангов | |||

| 
| по X | по Y | X–Y | (X–Y)2=d2 | |||
| 2,4 | – | – | ||||||
| 4,0 | – | – | 3,5 | –1,5 | 2,25 | |||
| 3,6 | – | – | ||||||
| 4,0 | – | – | 4,5 | 3,5 | ||||
| 4,5 | – | – | 4,5 | –0,5 | 0,25 | |||
| 4,6 | + | – | ||||||
| 5,6 | + | + | –1 | |||||
| 6,5 | + | + | –1 | |||||
| 7,0 | + | + | –1 | |||||
| 5,0 | + | + | ||||||
| Итого | 108 | 47,2 | x | x | 
| |||
| Средние | 10,8 | 4,72 | x | x |
U=9, V=1 = >  – связь прямая и высокая.
– связь прямая и высокая.
2. Коэффициент корреляции рангов (Спирмэна) определяется не по первичным данным, а по рангам (порядковым номерам), которые присваиваются всем значениям признаков в порядке их возрастания. Если значения признаков совпадают, то определяется средний ранг путем деления суммы рангов на число значений (см. таблицу исходных данных для определения коэффициента Фехнера).
 (7.14)
(7.14)
где ρ – коэффициент корреляции рангов;
d2 – квадрат разности рангов для каждой единицы наблюдения;
n – число единиц наблюдения;
ρ – изменяется от: –1 до +1.
Значения коэффициента Спирмэна идентичны коэффициенту Фехнера.
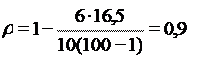 – связь прямая и высокая.
– связь прямая и высокая.
3. Коэффициент ассоциации (А) применяется для установления меры связи между двумя качественными альтернативными признаками. Для его вычисления строится комбинационная четырехклеточная таблица, которая выражает связь между двумя альтернативными признаками.
Пример. Определить зависимость наличия отдельной квартиры от семейного положения.
Таблица 7.5 – Состояние жилищного вопроса у различных категорий граждан в районе N в 2013 г.
| Семейное положение | Имеют отдельную квартиру, чел. | Не имеют отдельной квартиры, чел. | Всего |
| Семейные | 300 (а) | 115 (b) | 415 (a+b) |
| Одинокие | 15 (с) | 70 (d) | 85 (c+d) |
| Всего | 315 (а+с) | 185 (b+d) | 500 |
 (7.15)
(7.15)
Вывод: между семейным положением и обеспеченностью отдельной квартирой имеет место прямая умеренная связь.
4. Парный коэффициент корреляции применяется для определения силы связи для парной линейной зависимости (rху).
 (7.16)
(7.16)
или
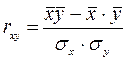 (7.17)
(7.17)
Парный коэффициент изменяется от -1 до +1
Если значение rху=+/- 1 – это функциональная зависимость;
а если rху=0 – связь отсутствует; rху>0 – связь прямая;
 – связь обратная.
– связь обратная.
В зависимости от значения коэффициентов корреляции различаются следующие виды связи между X и У.
Таблица 7.6 – Степень связи в соответствии с коэффициентом корреляции
| Значения, (r) | 0,99–0,9 | 0,9–0,7 | 0,7–0,5 | 0,5–0,3 | 0,3–0,1 | Менее 0,1 |
| Оценка тесноты связи | Весьма высокая | Высокая | Умеренная | Заметная | Слабая | Отсутствие связи |

Вывод: связь высокая прямая.
Между коэффициентом корреляции (парным) и параметрами линейного уравнения имеет место следующая зависимость:
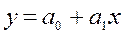
 (7.18)
(7.18)
 (7.19)
(7.19)
5. Коэффициент линейной корреляции (Rxy)
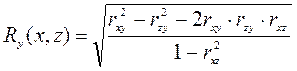 . (7.20)
. (7.20)
Если:
 ,
,  ,
, 
Тогда по формуле (7.20)
 .
.
Вывод: связь между потребителем мяса и факторами (доход на 1 члена семьи и число членов семьи) связь весьма высокая.
6. Корреляционное отношение
Применяется для определения степени тесноты связи для всех видов парной зависимости и линейных зависимостей:
 (7.21)
(7.21)
где η – корреляционное отношение;
yi – первоначальные эмпирические значения результативного показателя;
yрасч – теоретические значения результативного показателя, полученные по корреляционному уравнению;
 –среднее значение результативного показателя.
–среднее значение результативного показателя.
Изменяется показатель от 0 до 1, как и другие коэффициенты. Для таблицы 7.3 (по расчету потребления мяса) η =0,9531.