А.М. Пальти, доцент, кафедра общей и теоретической физики Физико-математического факультета Национального технического университета «КПИ» им. И.Сикорского
№4, 2017
ДЖЕЙМС КЛЕРК МАКСВЕЛЛ
(1831–1879)
Известно, что уравнения электромагнетизма Максвелла не изучают в школе, потому что для их формулировки нужна достаточно сложная математика теории поля. Но оказывается, что можно написать эти уравнения без применения интегралов и частных производных.
Попробуем сделать это, обобщая хорошо известные школьнику понятия работы силы или потока жидкости. Для этого нам потребуется определение скалярного произведения векторов, тоже известное из школы. При этом мы обобщим понятия работы силы на произвольную траекторию, а поток жидкости рассмотрим через произвольно расположенную в пространстве площадку.
Вообще, откуда возникло известное из математики понятие скалярного произведения векторов? Выскажем предположение, которое возможно имеет исторические корни. Не исключено, что само понятие работы силы, введенное Ж. Понселе в 1826 году, и было кандидатом на предка скалярного произведения. А скалярное произведение ввел У. Гамильтон в 1846 году. Кстати, он не только изобрел кватернионы, но и дал свою математическую формулировку законам механики.
Действительно, сила, действующая перпендикулярно смещению, не выполняет в этом направлении никакой работы. Только составляющая силы – проекция её на это направление – дает вклад в работу.
Таким образом, скаляр
Δ А = (F, Δ r) (1)
где Δ А – небольшая работа, выполненная на малом перемещении Δ r. А почему небольшая? Например, |Δ r | может быть и 1км. Важно только то, что на этом расстоянии постоянным должно быть произведение F ·Δ r ·cosα, где F, Δ r и α – модули силы, перемещения и угол между ними.
|
|
Если перемещение происходит в произвольном направлении в пространстве, выражение (1) записывают несколько иначе, и тогда указанную работу называют циркуляцией вектора F вдоль перемещения Δ r. Запишем это так:
Δ А ≡ Δ СF = (F, Δ r).
Для дальнейшего изложения нам потребуется ещё одно важное понятие - мы имеем в виду понятие векторного поля. Сначала немного истории. Ещё Ньютону не нравился его закон всемирного тяготения по причине его нелокальности - если в какой-то точке пространства исчезла масса (произошла «аннигиляция»), то мгновенно исчезает и сила. Было бы понятнее, если бы действие с какой-то скоростью переносилось через пространство от точки к точке. Чтобы как-то обосновать эту нелокальность, Ньютон ввел жёсткое абсолютное (и абсолютно жёсткое) пространство, которое мгновенно передает действие на любое расстояние. Правда, экспериментально обосновать существование абсолютного пространства так до сих пор и не удалось.
 МАЙКЛ ФАРАДЕЙ (1791–1867),
МАЙКЛ ФАРАДЕЙ (1791–1867),
АНГЛИЙСКИЙ ФИЗИК, ХИМИК, ОСНОВОПОЛОЖНИК
СОВРЕМЕННОЙ КОНЦЕПЦИИ ПОЛЯ В
ЭЛЕКТРОДИНАМИКЕ, АВТОР РЯДА ФУНДАМЕНТАЛЬНЫХ
ОТКРЫТИЙ, В ТОМ ЧИСЛЕ ЗАКОНА
ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ,
ЗАКОНОВ ЭЛЕКТРОЛИЗА, ЯВЛЕНИЯ ВРАЩЕНИЯ
ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА
В МАГНИТНОМ ПОЛЕ, ОДИН ИЗ ПЕРВЫХ
ИССЛЕДОВАТЕЛЕЙ ВОЗДЕЙСТВИЯ МАГНИТНОГО ПОЛЯ
НА СРЕДЫ. В МАТЕМАТИКЕ ВВЁЛ ПОНЯТИЯ
«ВЕКТОРНОЕ ПОЛЕ», «СИЛОВЫЕ ЛИНИИ».
Выход нашел великий английский физик Майкл Фарадей, который предложил идею векторного поля. Если в законе Кулона величину одного из зарядов принять за единицу, а другой считать источником поля, то закон можно трактовать так, что каждой точке пространства можно приписать силу, которая действует на этот единичный заряд. Так вводится поле сил.
|
|
В нашем случае силу в каждой точке пространства называют напряжённостью электрического поля. Имея такое поле (оно зависит только от заряда источника и его расстояния от точки наблюдения), легко найти силу, которая действует со стороны источника на заряд любой величины: F = q E (Q,r), где Q и r – заряд источника и расстояние от него точки наблюдения силы.
Если траектория проходит в пространстве, где есть заряды, то на ней существует поле электрических сил. Например, электродвижущая сила на участке электрического контура является циркуляцией вектора напряжённости электрического поля вдоль этого участка
Δ С Е = (Е, Δ r).
В этом случае, как очевидно из сравнения с (1), это работа по перемещению вдоль Δ r единичного положительного заряда.
Чтобы обобщить понятие «потока вектора», рассмотрим простой пример: воду, текущую в трубе. Пусть сначала скорость одинакова по всему сечению трубы (во всяком случае, всегда можно найти такой небольшой участок сечения, на котором скорость с определенной точностью постоянна). Понятно, что расход воды зависит от составляющей скорости вдоль оси трубы, а перпендикулярно к стенкам трубы вода не течет, поэтому составляющая скорости в этом направлении равняется нулю. Расход воды G через сечение трубы (в м3/с):
G = S ·v,
где S – значение площади сечения трубы, v – скорость вдоль её оси (скалярное произведение скорости воды и нормали к площадке).
|
|
Чтобы описать расход воды сквозь произвольно расположенную в пространстве площадку, обобщим понятие расхода введениям вектора площадки S, модуль которого равняется площади | S | = S, а направление совпадает с нормалью к площадке:

РИС. 1 И 2.
Тогда расход G можно определить как скалярное произведение:
∆ G ≡ ∆ F v = (v, ∆ S),
его ещё называют «потоком вектора v через площадку ∆ S». Как и в случае работы, это площадка, на которой произведение v·∆ S ·cosα можно считать постоянным.
В этом определении учитывается то обстоятельство, что скаляр ∆ F v – расход воды – обусловлен только составляющей скорости вдоль оси трубы. Заметим, что какое бы не было сечение трубы для расхода ∆ F v важное значение имеет только сечение, перпендикулярное к оси трубы.
Другой пример – электрический ток, который на языке введённых понятий есть поток вектора плотности тока j в проводнике через сечение ориентированной площадки ∆ S:
∆ І = ∆ F j = (j, ∆ S).
Если нужно найти полный поток сквозь поверхность (или циркуляцию вдоль определенного контура), то поле физической величины уже не является постоянным (на участке контура) и поэтому надо сложить отдельные потоки ∆ FAi (или циркуляции ∆ CAi):
FA = ∆ FA1 + ∆ FA2 +…+ ∆ FAn или CA = ∆ CA1 + ∆ CA2 +…+ ∆ CAn.
(заметим, что высшая математика имеет для этих сумм специальное название – определённый интеграл).
После проведённой подготовки уже несложно написать все уравнения электромагнитного поля Максвелла. Начнем с теоремы Гаусса, которая обобщает закон Кулона, её формулировка: поток вектора напряжённости электрического поля сквозь замкнутую поверхность равняется сумме зарядов qі, расположенных внутри неё (см. рис.3):
| F E = (Е 1∆S1 + Е 2∆S2 + …) = (q 1 + q 2 +...)/εо = q/εо, |
где εо – электрическая постоянная; Е 1, Е 2, … – значения напряжённости в определённых точках поверхности оболочки; ∆ S 1, ∆ S 2, … – площадки возле этих точек, покрывающие всю поверхность оболочки, где модули произведений | Е 1∆ S 1|, | Е 2∆ S 2|, … постоянны, q – полный заряд внутри оболочки.
Следующее уравнение касается вектора магнитной индукции. Известно, что магнитных зарядов не существует, и это учитывается законом: поток вектора индукции магнитного поля В сквозь замкнутую оболочку равняется нулю:
| F B = (В 1Δ r 1 + В 2Δ r 2 + …) = 0. |
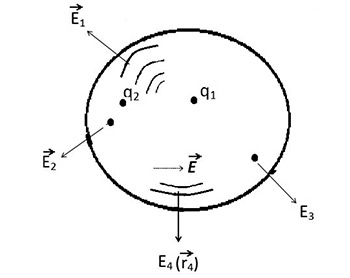
РИС. 3.
Дальше сформулируем закон электромагнитной индукции Фарадея: циркуляция вектора напряжённости электрического поля вдоль любого связного (не имеющего вида «восьмерки») замкнутого контура Г равняется средней скорости уменьшения в единицу времени потока вектора индукции магнитного поля (обозначим эту скорость как ∆1) сквозь односвязную поверхность S, натянутую на этот контур:
| C E = – ∆ F B /∆ t. |
Немного сложнее (но не очень) формулируется ещё одно уравнение Максвелла - обобщение закона полного тока Ампера. Максвелл заметил, что в разомкнутой цепи переменного тока (например, которая содержит конденсатор) нужно учитывать воображаемый ток (по аналогии с поляризацией зарядов его называют током смещения), который обусловлен изменением заряда на обкладках конденсатора. Тогда последнее уравнение Максвелла можно сформулировать так: циркуляция вектора индукции магнитного поля вдоль некоторого замкнутого контура, который охватывает провода с током и конденсаторы, равна суммарному потоку плотности этих токов плюс средней скорости изменения потока вектора напряжённости электрического поля
| C B = µо(F j + εо∆ F E /∆ t) |
где εо и µо – электрическая и магнитная постоянные. Таким образом, полная система уравнений Максвелла в системе единиц SІ выглядит так:
F E = q/εо,
F B = 0.
C E = – ∆ F B /∆ t,
C B = µо(Fj + εо∆ F E /∆t).