Фарадей в своём письме, которое он просил открыть через 106 лет, пишет о том, что свет имеет электромагнитную природу и распространяется со скоростью 300 000 км/с. Этот результат Максвелл получил из своих уравнений уже через 10 лет после указанного завещания. Но чтобы написать волновое уравнение, из которого следует этот замечательный результат, нужно применить к уравнениям (1) – (4) уже немного больше математики - как раз те самые производные и интегралы.
В предсказании электромагнитных волн Максвелл обогнал своё время. Но он не мог знать того, что ещё в 1832 году Майкл Фарадей оставил в Лондонском королевском обществе для хранения в архиве запечатанный конверт с надписью "Новые воззрения, подлежащие хранению в архивах Королевского общества".
 МАЙКЛ ФАРАДЕЙ ЗА ОПЫТАМИ В ЛАБОРАТОРИИ
МАЙКЛ ФАРАДЕЙ ЗА ОПЫТАМИ В ЛАБОРАТОРИИ
Лишь через сто шесть лет в 1938 году этот конверт был вскрыт английскими учёными. На пожелтевшем листке содержались слова и мысли, которые потрясли всех собравшихся. Оказалось, что Фарадей уже ясно представлял себе то, что "индуктивные явления распространяются в пространстве с некоторой скоростью в виде волн". В этом бумажном листке от 12 марта 1832 года он написал: "Я пришёл к заключению, что на распространение магнитного воздействия требуется время, которое, однако, окажется весьма незначительным. Я полагаю также, что электрическая индукция распространяется точно таким же образом. Я полагаю, что распространение магнитных сил от магнитного полюса похоже на колебания взволнованной водной поверхности. По аналогии, я считаю возможным применить теорию колебаний к распространению электрической индукции. В настоящее время, насколько мне известно, никто из учёных, кроме меня, не имеет подобных взглядов".
P.S.
ДЖОРДЖ ГАБРИЕЛЬ СТОКС (1819 –1903),
АНГЛИЙСКИЙ МАТЕМАТИК, МЕХАНИК И
ФИЗИК-ТЕОРЕТИК ИРЛАНДСКОГО ПРОИСХОЖДЕНИЯ.
РАБОТАЛ В КЕМБРИДЖСКОМ УНИВЕРСИТЕТЕ,
ВНЁС ЗНАЧИТЕЛЬНЫЙ ВКЛАД В ГИДРОДИНАМИКУ И
ГАЗОДИНАМИКУ, ОПТИКУ И МАТЕМАТИЧЕСКУЮ
ФИЗИКУ. БЫЛ ЧЛЕНОМ МНОГИХ АКАДЕМИЙ,
В ТОМ ЧИСЛЕ ВОЕННО-МЕДИЦИНСКОЙ АКАДЕМИИ
В ПЕТЕРБУРГЕ.
Когда настоящая статья уже была принята к публикации, редактор заметил автору: работа, конечно, интересная, но есть какое-то впечатление незавершенности - чего-то не хватает. В самом деле, всё изложение построено только на двух основных понятиях: циркуляции вектора вдоль контура и потока вектора через площадку. Вроде бы разные понятия, но в основе обоих лежит скалярное произведение! Связаны ли они каким-то образом? Оказывается, такая связь существует.
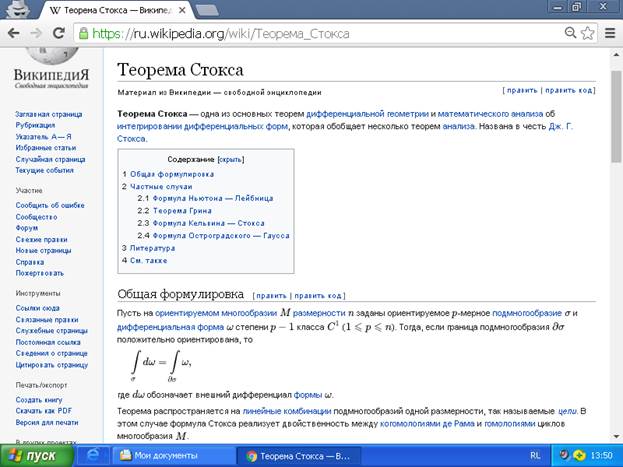
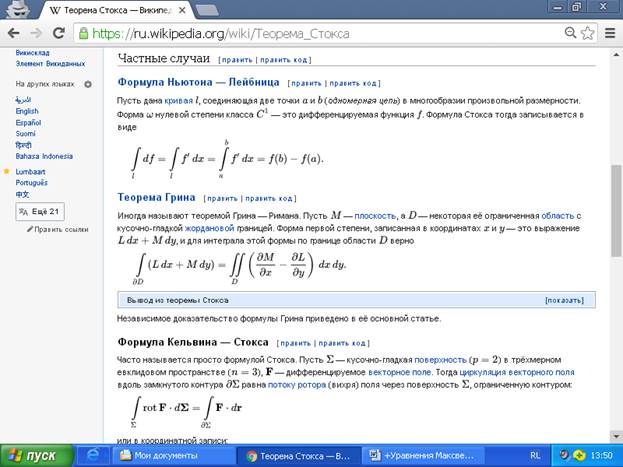
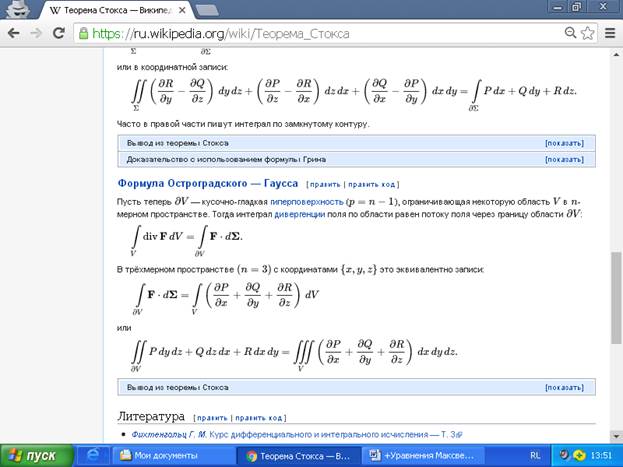
Если задано поле векторов (в каждой точке пространства задан вектор), причём любой природы (не только электрической), то имеет место замечательная теорема Стокса: циркуляция вектора вдоль любой замкнутой связной (без самопересечений) линии равна потоку этого векторного поля через замкнутую поверхность с границей в виде этой линии (контура). При этом форма поверхности не имеет значения (свойство скалярного произведения). Это доказывается в математике. В простом случае, когда контур - окружность на плоскости, то соответствующая поверхность – это внутренность ограниченного ею круга. Интересно, что Джордж Стокс, видимо, считал указанную теорему достаточно простой и поэтому не опубликовал её доказательства. Но он использовал её в качестве вопроса к конкурсным экзаменам для студентов-математиков Кембриджского университета. Позже (и это, видимо, справедливо) за теоремой закрепилось его имя (примерно в 1850 году). Сегодня известно много доказательств этой, уже существенно обобщённой, теоремы с тем же именем.