 Этот метод похож на предыдущиу. Отличие в том, что высота прямоугольников вычисляется по правой границе (Рис. 3). Выводы формул для данного метода аналогичны предыдущему.
Этот метод похож на предыдущиу. Отличие в том, что высота прямоугольников вычисляется по правой границе (Рис. 3). Выводы формул для данного метода аналогичны предыдущему.
Основные отличия заключаются в нумерации. Формула метода правых прямоугольников выглядит следующим образом: 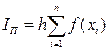 .
.
Метод средних прямоугольников
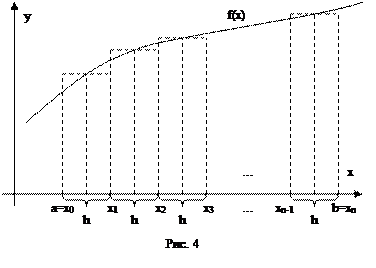 Чтобы уменьшить погрешность методов левых и правых прямоугольников был предложен метод средних, т.е. метод в котором высота прямоугольника вычисляется в середине отрезка h (Рис. 4). Обращаясь к рисунку легко увидеть, что площади прямоугольников вычисляются по следующим формулам:
Чтобы уменьшить погрешность методов левых и правых прямоугольников был предложен метод средних, т.е. метод в котором высота прямоугольника вычисляется в середине отрезка h (Рис. 4). Обращаясь к рисунку легко увидеть, что площади прямоугольников вычисляются по следующим формулам:
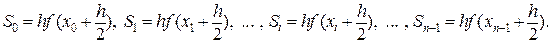
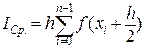
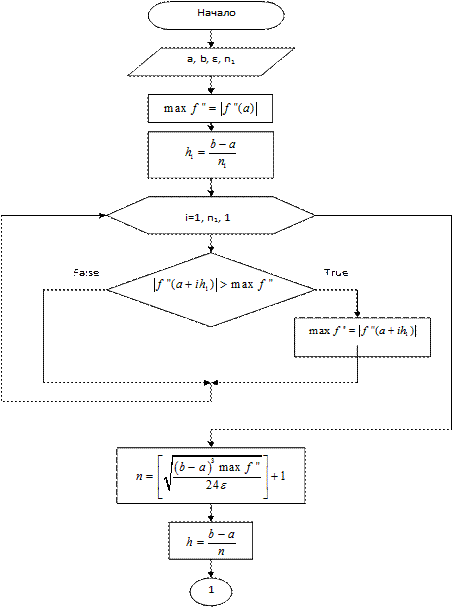
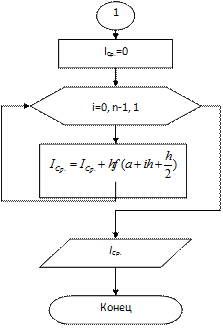
Построим блок-схему для метода средних прямоугольников, так как он во много раз точнее и для достижения заданной точности требует меньше машинного времени. Введём обозначение. [n] – целая часть n, полученная путём отбрасывания дробно части. Для вычисления интеграла дано ε, [a,b], f(x), f’’(x). Прежде всего, через ε необходимо получить n. Для этого перед вычислением интеграла необходимо найти 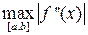 , но это легко осуществимо с помощью небольшого циклического процесса. Для него понадобиться знание количества разбиений
, но это легко осуществимо с помощью небольшого циклического процесса. Для него понадобиться знание количества разбиений 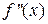 , на которых будем вычислять значения второй производной. Обозначим это количество n1.
, на которых будем вычислять значения второй производной. Обозначим это количество n1.
2.3. Пример выполнения последнего варианта в Mathcad
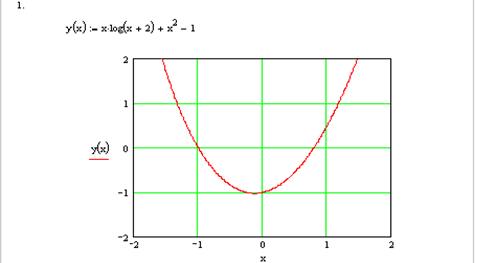
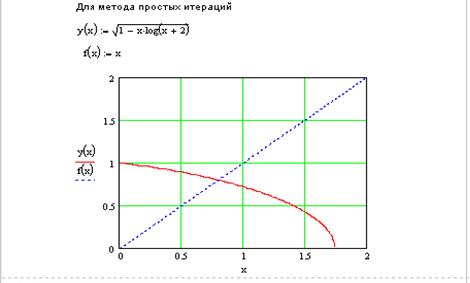
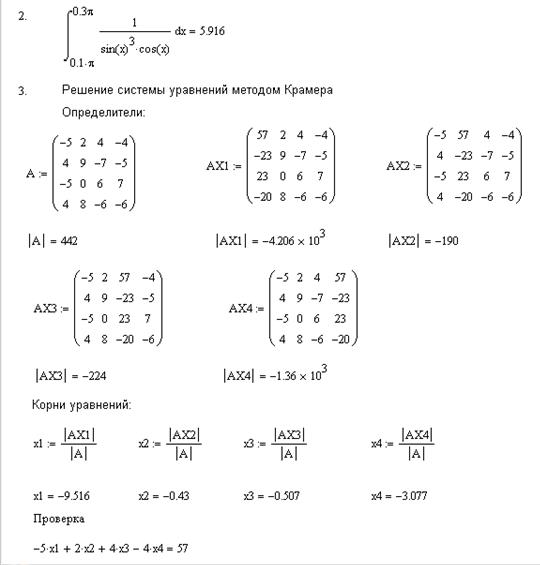
Варианты заданий для контрольной работы
Задание № 1 Методом Крамера и Гаусса решить системы линейных алгебраических уравнений с точностью 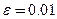 . Сравнить точность результатов полученных разными методами и значений в Mathcad.
. Сравнить точность результатов полученных разными методами и значений в Mathcad.
1. 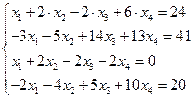 2.
2. 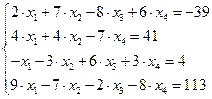
3. 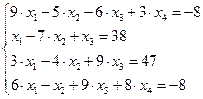 4.
4. 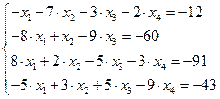
5. 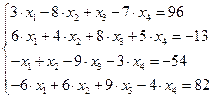 6.
6. 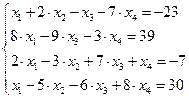
7. 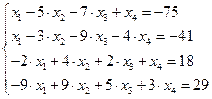 8.
8. 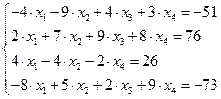
9. 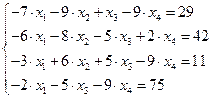 10.
10. 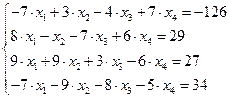
11. 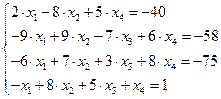 12.
12. 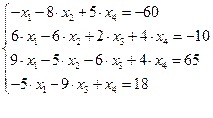
13. 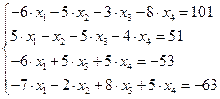 14.
14. 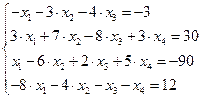
15. 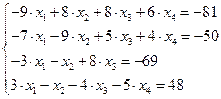 16.
16. 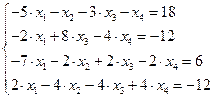
17. 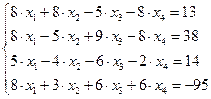 18.
18. 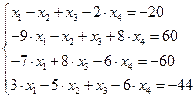
19. 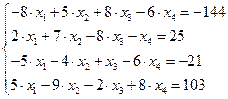 20.
20. 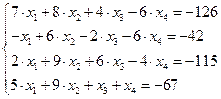
21. 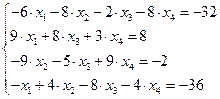 22.
22. 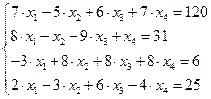
23. 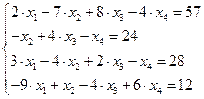 24.
24. 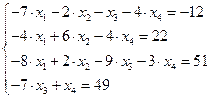
25. 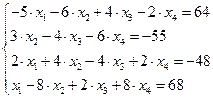 26.
26. 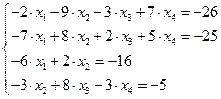
27. 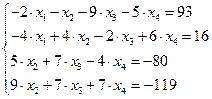 28.
28. 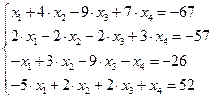
29. 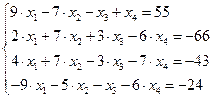 30.
30. 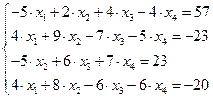
Задание №2 С помощью программы для ЭВМ с точностью 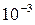 методами простых итераций, дихотомии, касательных (Ньютона) и секущих найти положительный корень нелинейного уравнения. Начальное приближение определить графически. (В случае невозможности применить какой-либо метод, объяснить причины неприменимости данного метода). Сравнить точность результатов полученных разными методами и значений в Mathcad.
методами простых итераций, дихотомии, касательных (Ньютона) и секущих найти положительный корень нелинейного уравнения. Начальное приближение определить графически. (В случае невозможности применить какой-либо метод, объяснить причины неприменимости данного метода). Сравнить точность результатов полученных разными методами и значений в Mathcad.
1.  2.
2. 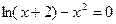 3.
3. 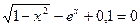 4.
4. 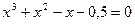 5.
5. 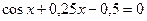 6.
6. 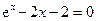 7.
7. 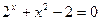 8.
8. 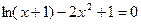 9.
9. 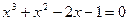 10.
10. 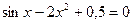 11.
11. 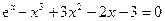 12.
12. 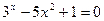 13.
13. 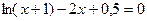 14.
14. 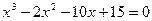 15.
15. 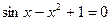
| 16.  17.
17. 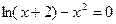 18.
18. 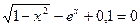 19.
19. 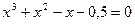 20.
20. 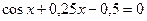 21.
21. 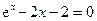 22.
22. 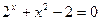 23.
23. 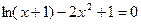 24.
24. 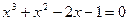 25.
25. 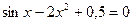 26.
26. 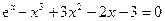 27.
27. 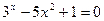 28.
28. 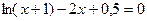 29.
29. 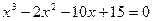 30.
30. 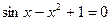
|
Задание № 3 Составить программу и вычислить на ЭВМ интеграл заданной функции 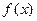 на отрезке
на отрезке 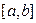 с точностью
с точностью 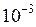 методами прямоугольников, трапеций. Сравнить точность результатов полученных разными методами и значение интеграла решенного в Mathcad.
методами прямоугольников, трапеций. Сравнить точность результатов полученных разными методами и значение интеграла решенного в Mathcad.
| Вариант | Подынтегральная функция
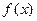
| Пределы интегрирования a b | |
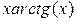
| 6,5 | ||
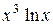
| 3,5 | ||
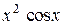
| 3 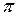
| 3,5 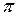
| |
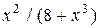
| |||
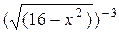
| 0,5 | ||
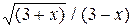
| 2,5 | ||
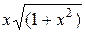
| |||
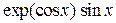
| 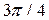
| 2 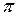
| |
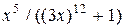
| |||
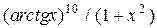
| 0,2 | 0,3 | |
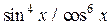
| 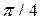
| ||
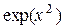
| |||
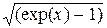
| 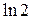
| ||
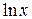
| |||
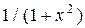
| |||
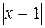
| |||
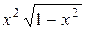
| |||
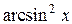
| 0,5 | ||
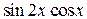
| 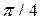
| ||
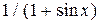
| 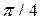
| ||
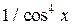
| 0,1 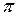
| 0,5 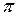
| |
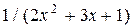
| |||
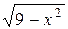
| |||
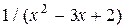
| |||
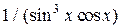
| 0,1 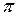
| 0,3 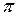
| |
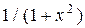
| |||
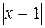
| |||
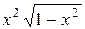
| |||
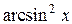
| 0,5 | ||
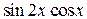
| 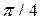
|
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Александрова, В. О. Вычислительная математика: учеб. пособие / В. О. Александрова; ВолгГТУ, ВПИ (филиал) ВолгГТУ. - Волгоград: РПК "Политехник", 2007. - 159 с.
2. Вычислительная математика (для студентов технических направлений) [Электронный ресурс]: учеб. пособие / И. В. Ребро, Д. А. Мустафина; ВПИ (филиал) ВолгГТУ// Сборник "Учебные пособия". Серия "Технические дисциплины". Вып. 1. - Волгоград, 2013. – 86 с.
3. Специализированные программные средства для проведения инженерных расчётов. Лабораторный практикум: учеб. пособие / Е.С. Павлова, В.С. Поляков, И.Г. Лемешкина, М.Г. Скворцов; ВолгГТУ. - Волгоград, 2014. - 95 с.
4. Тарасова, И.А. Методы оптимизации: учеб. пособие / И.А. Тарасова, И.Э. Симонова, А.Б. Симонов; ВолгГТУ. - Волгоград, 2015. - 96 с.
Учебное издание
Лидия Викторовна Дружинина