4.18 (7 б.) В массиве Z(2n) каждый элемент с четным индексом поменять местами с предыдущим, то есть получить последовательность чисел z2, z1, z4, z3,… z2n, z2n-1.
4.22 (9 б.) Плюсы и минусы. В массиве Z(m) найти число чередований знака, то есть число переходов с минуса на плюс или с плюса на минус. Например, в последовательности 0,-2,0,-10, 2,-1,0,0,3,2,-3 четыре чередования (как известно, нуль не имеет знака).
4.23 (8 б.) Латинский квадрат. Латинским квадратом порядка n называется квадратная таблица размером n×n, каждая строка и каждый столбец которой содержит все числа от 1 до n. Для заданного n в матрице L(n,n) построить латинский квадрат порядка n.
4.24 (7 б.) Нарастающий итог. В массиве A(n) каждый элемент, кроме первого, заменить суммой всех предыдущих элементов.
4.25 (7 б.) Разные соседи. Заполнить матрицу заданного размера M(k,l) числами 1,2,3,4 так, чтобы по горизонтали, вертикали и диагонали не было одинаковых рядом стоящих чисел.
4.26 (8 б.) Король и ферзи. На шахматной доске находятся король и несколько ферзей другого цвета. Проверить, находится ли король под угрозой и если да, кто ему угрожает. Положение фигур задано массивом K(8,8): 0 – клетка пуста, 1 – король, 2 – ферзь.
4.27 (7 б.) Сессия. Результаты сессии, состоящей из трех экзаменов, для группы из n студентов представлены матрицей K(n,3). Оценка ставится по четырехбалльной системе; неявка обозначается единицей. Подсчитать количество неявок, неудовлетворительных, удовлетворительных, хороших и отличных оценок по каждому экзамену.
4.28 (7 б.) Текущее сглаживание. Каждый из элементов xi массива X(n)
заменить средним значением первых i элементов этого массива.
4.29 (7 б.) Текущий минимум. Каждый из элементов ti массива T(m) заменить минимальным среди первых i элементов этого массива.
4.30 (8 б.) Турнирная таблица. В матрице K(n,n) представлена турнирная таблица соревнований по футболу среди n участников (каждый элемент aij матрицы есть число голов, забитых i-м участником j-му участнику); все элементы главной диагонали равны нулю. Присвоить каждому диагональному элементу разницу забитых и пропущенных голов соответствующего участника, то есть разность между суммами элементов соответствующих строки и столбца.
4.31 (8 б.) Циклический сдвиг. Осуществить циклический сдвиг элементов массива T(n) на m позиций влево, то есть получить массив: tm+1,…,tn,t1,…,tm. При этом необязательно m<n.
4.32 (9 б.) Суммы по косой. Просуммировать элементы матрицы A(n,n) по каждой из линий, параллельных главной диагонали. Напечатать полученные суммы.
5.2 (8 б.) Улитка. Матрицу M(m,n) заполнить натуральными числами от 1 до m·n по спирали, начинающейся в левом верхнем углу и закрученной по часовой стрелке.
5.4 (7 б.) Куб состоит из n3 прозрачных и непрозрачных элементарных кубиков. Имеется ли хотя бы один просвет по каждому из трех измерений? Если это так, вывести координаты каждого просвета.
Рекомендация. Для хранения кубика выделить трехмерный массив с базовым типом минимально возможного размера, так как значениями его будут только единицы или нули. При тестировании полезно использовать рандомизацию – случайным образом присвоить элементам 0 или 1, возможно, с указанием вероятности тех и других, с последующей послойной распечаткой.
5.5 (8 б.) Используя ту же структуру данных, что и в предыдущей задаче, построить полностью непрозрачный куб, используя ровно n2 непрозрачных элементарных кубиков.
5.6 (8 б.) В матрице A(m,n) каждый элемент aij заменить минимальным среди элементов подматрицы A’(i,j), расположенной в левом верхнем углу матрицы А.
5.7 (8 б.) Нарастающий итог. Каждый элемент aij матрицы A(m,n) заменить суммой элементов подматрицы A’(i,j), расположенной в левом верхнем углу матрицы А.
5.11 (7 б.) Задача Иосифа [20]. По кругу располагаются n человек. Ведущий считает по кругу, начиная с первого, и выводит («казнит») m-го человека. Круг смыкается, счет возобновляется со следующего после «казненного»; так продолжается, пока «в живых» останется только один человек. Найти номер оставшегося «в живых» человека, а также для заданного n найти такое m>1, при котором «в живых» останется первый.
5.13 (8 б.) Работа комбайнера. Матрицу K(m,n) заполнить следующим образом. Элементам, находящимся на периферии (по периметру матрицы), присвоить значение 1; периметру оставшейся подматрицы – значение 2 и так далее до заполнения всей матрицы.
5.16 (9 б.) Замочная скважина. Даны мозаичные изображения замочной скважины и ключа. Пройдет ли ключ в скважину? То есть даны матрицы K(m1,n1) и L(m2,n2), m1>m2, n1>n2, состоящие из нулей и единиц. Проверить, можно ли наложить матрицу L на матрицу K (без поворота, разрешается только один сдвиг) так, чтобы каждой единице матрицы L соответствовал нуль в матрице K, и если можно, то как (на сколько и в каком направлении следует подвинуть матрицу L по матрице K до выполнения условия)?
(12 б.) Развитие задачи. «Ключ» разрешается поворачивать на угол, кратный 90°; его можно также зеркально отображать.
5.22 (6 б.) Касса. В массиве K(n) в порядке убывания представлены достоинства денежных знаков (купюр и монет) валютной системы некоторой страны. Реализовать выдачу в этой системе заданной суммы m минимальным числом денежных знаков.
5.23 (10 б.) Соседи. Из элементов массива A(2n) получить массивы B(n) и C(n) следующим образом. Выбрать в массиве А два наиболее близких по значению элемента; меньший из них поместить в массив В, а больший – в массив С. Продолжить выбор их оставшихся элементов до полного заполнения массивов В и С.
5.24 (8 б.) Колокол. В массиве A(n) наименьший элемент поместить на первое место, наименьший из оставшихся – на последнее место, следующий по величине – на второе место, следующий – на предпоследнее и так далее – до середины массива.
5.25 (7 б.) Матрица K(m,m) состоит из нулей и единиц. Найти в ней номера (индексы) хотя бы одной строки или хотя бы одного столбца, не содержащих единицы, либо сообщить, что таковых нет.
5.31 (8 б.) Магический квадрат. Магическим квадратом порядка n называется квадратная таблица размером n×n, состоящая из чисел 1,2,…, n2 так, что суммы по каждому столбцу, каждой строке и каждой из двух диагоналей равны между собой. Проверить, является ли заданная целочисленная квадратная матрица магическим квадратом.
6.4 (8 б.) Поле размером m×n заполнено прозрачными и непрозрачными кубиками. Найти все столбцы поля, все непрозрачные кубики которых невидимы для наблюдателя, расположенного слева.
6.5 (9 б.) Поле размером m×n заполнено прозрачными и непрозрачными кубиками. Удалить (сделать прозрачными) все непрозрачные кубики, видимые хотя бы с одной их четырех сторон (видимость анализируется до удаления какого-либо кубика).
6.6 (10 б.) В заданном массиве A(n) найти i и j такие, что  максимально.
максимально.
6.7 (8 б.) В массиве А(l), все элементы которого различны, найти и удалить n наименьших элементов, «поджимая» массив к началу и сохраняя порядок следования остальных элементов (n<<l).
6.8 (7 б.) В массиве T(k) найти первый и последний нулевые элементы.
6.9 (7 б.) В массиве L(m) найти наиболее длинную цепочку, состоящую из одних нулей.
6.10 (10 б.) Матрица L(n,k) состоит из нулей и единиц. Найти в ней самую длинную цепочку подряд стоящих нулей по горизонтали, вертикали или диагонали.
6.11 (9 б.) В целочисленном массиве K(n) много повторяющихся элементов. Найти (в процентах) частоту появления каждого из m наиболее часто встречающихся элементов (m<<n).
6.12 (8 б.) Даны два целочисленных массива K(m) и L(n). Найти наибольший элемент массива K, не имеющий себе равных в массиве L.
6.13 (8 б.) Среди элементов массива Z(m) найти k (k<<m) наибольших. Поиск осуществить за один проход (просмотр) массива Z.
6.14 (7 б.) В целочисленном массиве L(n) найти наиболее длинную цепочку одинаковых подряд стоящих элементов.
6.15 (9 б.) В массиве M(k) много совпадающих элементов. Найти количество различных элементов в нем (не упорядочивая массива).
7.1 (8 б.) Натуральное число в p-ичной системе счисления задано своими цифрами, хранящимися в массиве K(n). Проверить корректность такого представления и перевести число в q-ичную систему (возможно, число слишком велико, чтобы получить его внутреннее представление; кроме того, p  10, q
10, q  10).
10).
7.16 (9 б.) Перевести заданное целое число в систему римского счета.
Указание. Римские цифры обозначаются следующими латинскими буквами:
| I | D | ||
| V | M | ||
| X | 
| ||
| L | 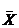
| ||
| C | … | … |
7.21 (10 б.) Произведение двух заданных натуральных чисел больше максимально допустимого значения (не вмещается в разрядную сетку машины). Найти это произведение.
7.32 (7 б.) Число Армстронга – такое число из k цифр, для которого сумма k-х степеней его цифр равна самому числу, например: 153=13+53+33. Найти все числа Армстронга не более чем из четырех цифр.
7.37 (9 б.) Натуральное число называется совершенным, если оно равно сумме всех своих простых делителей (например, 6=1+2+3). Найти все совершенные числа, не превосходящие заданного n.
Примечание. На сегодня известно 24 совершенных числа; все они четные. Вопрос о конечности множества совершенных чисел открыт.
7.49 (7 б.) Имеется набор гирь весом 1,2,5,10,20,50,100,… грамм. Как взвесить тело заданной массы m г на равноплечих весах, используя минимальное число гирь?
(10 б.) Развитие задачи. Имеется лишь по одной гире каждого номинала. Разрешается класть гири на любую чашку весов. Как уравновесить тело, используя минимальное число гирь? Например, масса 27 г уравновешивается: 27+1+2=10+20 либо 27+1+2+20=50.
10.27 (12 б.) 12 монет. Известен способ, как за три взвешивания на весах без гирь среди 12 монет найти фальшивую (отличающуюся от остальных по весу в неизвестную сторону). Для этого при каждом взвешивании на чаши весов нужно класть по 4 монеты. Реализовать такую идентификацию: человек загадывает номер фальшивой монеты и ее особенность (легче или тяжелее других). ЭВМ организует взвешивание, спрашивает, куда отклонилась стрелка весов при каждом опыте, и находит номер фальшивой монеты.
(12 б.) Развитие задачи. Реализовать идентификацию за минимальное число взвешиваний для произвольного числа монет.
12.10 (7 б.) Заданный список русских фамилий (вместе с именами и отчествами) упорядочить по алфавиту. Проверить (и исправить, если нужно) написание собственных имен с прописных букв.
12.11 (8 б.) В заданном тексте подсчитать частоту использования каждого буквосочетания, слова и словосочетания из заданного списка.
12.12 (10 б.) В заданном тексте найти самое длинное слово и самую длинную фразу.
12.13 (7 б.) Морзянка. Вводимый с клавиатуры или из файла текст перевести в последовательность точек и тире с помощью азбуки Морзе. Результат можно иллюстрировать звуком.
Для справки – азбука Морзе:
| А, А | .- | Б, B | -… | В, W | .-- | Г, G | --. | Д, D | -.. |
| Е, Ё,E | . | Ж, V | …- | З, Z | --.. | И, I | .. | Й, J | .--- |
| К, K | -.- | Л, L | .-.. | М, M | -- | Н, N | -. | О, O | --- |
| П, P | .--. | Р, R | .-. | С, S | … | Т, T | - | У, U | ..- |
| Ф, F | ..-. | Х, H | …. | Ц, C | -.-. | Ч | ---. | Ш | ---- |
| Щ, Q | --.- | Ъ | .--.-. | Ы, Y | -.-- | Ь, X | -..- | Э | …-… |
| Ю | ..-- | Я | .-.- | .---- | ..--- | …-- | |||
| ….- | ….. | -…. | --… | ---.. | |||||
| ----. | ----- | . | .-.-.- | , | --..-- | : | ---… | ||
| ? | ..--.. | ‘,’ | .----. | - | -….- | / | -..-. | , | -.--.- |
12.17 (6 б.) Имеется большой словарь русских слово. Найти в нем слова-палиндромы («перевертыши»), одинаково читающиеся как слева направо, так и справа налево, например, АННА, ШАЛАШ и так далее.
(10 б.) Развитие задачи. В словаре встречаются не только слова-палиндромы, но и фразы-палиндромы, например: «А роза упала на лапу Азора». Найти и их.
12.27 (9 б.) Перенос. Примем следующие правила переноса русских слов:
· в каждой из разделяемых частей должно быть более одной буквы, из которых хотя бы одна – гласная;
· нельзя разделять согласную и следующую за ней гласную;
· буквы Й, Ь, Ъ считать согласными, но перенос после них допустим.
В каждом из вводимых слов поставить все возможные знаки переноса, например: СЕ-ЛЬ-С-КО-ХО-ЗЯЙ-С-Т-ВЕ-Н-НА-Я. Строчные и прописные буквы считать неразличимыми.
12.28 (8 б.) По правилам пунктуации пробел может стоять после, а не перед каждым из следующих знаков:.,;:!?) ] } …; перед, а не после знаков: ([ {. Заданный текст проверить на соблюдение этих правил и при необходимости исправить. Вместо пробела может быть перевод строки или знак табуляции.
12.29 (7 б.) Скобки. Текст (например, арифметическое выражение) содержит многократно вложенные круглые скобки. Исправить его, оставив скобки первого уровня круглыми, второго – заменить на квадратные, третьего и последующих – на фигурные. Убедиться в корректности использования скобок.
Пример. ln(sin((a+b)c-d)) заменить выражением ln{sin[(a+b)c-d]}.