Обнаружение гетероскедастичности
Одной из предпосылок регрессионного анализа является предположение о постоянстве дисперсии случайного члена для всех наблюдений (гомоскедастичность). Это значит, что для каждого значения объясняющей переменной случайные члены имеют одинаковые дисперсии. Если это условие не соблюдается, то имеет место гетероскедастичность.
При отсутствии гетероскедастичности коэффициенты регрессии имеют наименьшую дисперсию среди всех несмещенных оценок, являющихся линейными функциями от наблюдений y.
Если наблюдается гетероскедастичность, то МНК-оценки будут неэффективными (они не будут иметь наименьшую дисперсию по сравнению с другими оценками этого параметра).
Оценки стандартных ошибок коэффициентов регрессии вычисляются в предположении, что распределение случайного члена гомоскедастично; если это не так, то они неверны (занижены), а, следовательно, t -статистика – завышена. Это может привести к статистически значимым коэффициентам регрессии, тогда как в действительности это не так.
Проблема гетероскедастичности характерна для пространственных данных, полученных от неоднородных объектов. Например, если исследуется зависимость прибыли предприятий от размера основного фонда, то можно ожидать, что для больших предприятий колебание прибыли будет выше, чем для малых.
Предложено большое число тестов для обнаружения гетероскедастичности, в которых делаются различные предположения о зависимости между дисперсией случайного члена и величиной объясняющей переменной (или объясняющих переменных), например, тест ранговой корреляции Спирмена, тест Голдфелда-Квандта и тест Глейзера.
Тест ранговой корреляции Спирмена
Выдвигается нулевая гипотеза об отсутствии гетероскедастичности случайного члена. При выполнении теста ранговой корреляции Спирмена предполагается, что дисперсия случайного члена будет либо увеличиваться, либо уменьшаться по мере увеличения x, и поэтому в регрессии, оцениваемой с помощью МНК, абсолютные величины остатков | e | и значения x будут коррелированы.
Данные по x и остатки | e | ранжируются по переменной x, и определяются их ранги.
Ранг – это порядковый номер значений переменной в ранжированном ряду.
Коэффициент ранговой корреляции Спирмена определяется по формуле:
,
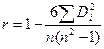где Di – разность между рангами x и | e |.
Если предположить, что коэффициент корреляции для генеральной совокупности равен нулю, то коэффициент ранговой корреляции имеет нормальное распределение с нулевым математическим ожиданием и дисперсией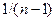 
в больших выборках. Соответствующая тестовая статистика 
сравнивается с критическим значением t кр при заданном уровне значимости (t кр =1,96 при a = 5%, t кр = 2,58 при a = 1 %).
Если > t кр, то нулевая гипотеза об отсутствии гетероскедастичности будет отклонена.
Если в модели регрессии имеется более одной объясняющей переменной, то проверка гипотезы может выполняться с использованием любой из них.
Пример 1.1. Оценим регрессионную зависимость выпуска продукции обрабатывающей промышленности на душу населения y от валового внутреннего продукта на душу населения x в том же году для 17 стран.
Исходные данные (усл. ед.):
| n | y | x | n | y | x |
В таблице наблюдения расположены в порядке возрастания независимой переменной x.
Пусть модель описывается выражением y = a + bx + e.
По исходным данным с помощью МНК получена следующая регрессионная зависимость:
(1.1)
(в скобках указаны стандартные ошибки).
Рис. А. Результаты инструмента Регрессия пакета Анализа данных
Рис. 1. График остатков ei, полученный инструментом Регрессия
Из рисунка видно, что с увеличением переменной x размах колебаний остатков e тоже возрастает, поэтому есть предположение о зависимости ошибки регрессии от независимой переменной (гетероскедастичность).
Для установления гетероскедастичности применим тест Спирмена.
Выдвигается нулевая гипотеза об отсутствии гетероскедастичности.
Отклонения от линии регрессии (остатки e) и данные по x в порядке возрастания приведены в следующей таблице:
| X | Ранг | | ei | | Ранг | Di | Di 2 | X | ранг | | ei | | Ранг | Di | Di 2 |
| 3,6 | -1 | 17,1 | |||||||||
| 3,3 | 22,8 | ||||||||||
| 15,2 | -6 | 41,2 | -3 | ||||||||
| 5,9 | 43,3 | -3 | |||||||||
| 4,2 | 34,5 | ||||||||||
| 11,4 | -1 | 45,0 | -2 | ||||||||
| 14,4 | -1 | 40,8 | |||||||||
| 9.8 | 38,7 | ||||||||||
| 7,9 | Итого |
Здесь значения | ei | взяты из результата инструмента Регрессия (рис. Б).
Рис. Б
Чтобы ранжировать остатки, необходимо выполнить следующие действия.
Скопировать остатки. Рассчитать их модули (функция ABS из категории Математические). Выполнить сортировку. Использовать функцию Ранг из категории Статистические (рис. В).
Рис. В
На основе этих данных вычислен коэффициент ранговой корреляции:
0,865196078
Тестовая статистика составляет 
. Это выше, чем t 0,05;15 = 2,13 (СТЬЮДРАСПОБР) и, следовательно, нулевая гипотеза об отсутствии гетероскедастичности отклоняется.
Тест Голфельда-Квандта
При проведении проверки по этому тесту предполагается, что стандартное отклонение s случайного члена пропорционально значению независимой переменной x.
Тест включает следующие шаги:
1) Все n наблюдений в выборке упорядочиваются по возрастанию переменной x.
2) Оцениваются отдельные регрессии для первых n 0 и для последних n 0наблюдений. Средние (n – 2 n 0) наблюдений отбрасываются.
3) Составляется статистика: F = RSS2 /RSS1, где RSS1, RSS2 – суммы квадратов остатков для первых и последних n 0 наблюдений соответственно.
Если верна гипотеза H 0 об отсутствии гетероскедастичности, то F имеет распределение Фишера с v 1 = k, v 2= n 0 – k – 1 степенями свободы, где k – число объясняющих переменных.
По таблице определяется критическое значение критерия F кр.
Если F > F кр, то нулевая гипотеза об отсутствии гетероскедастичности отклоняется.
Замечание. Тест Голфельда-Квандта можно также использовать для проверки на гетероскедастичность при предположении, что si обратно пропорционально xi. В этом случае тестовой статистикой является величина F = RSS1 /RSS2.
Пример 1.2. На основе данных примера 1.1 с помощью обычного МНК оценим регрессии для шести стран с наименьшими значениями показателя x и для шести стран с наибольшими значениями этого показателя.
Получены, соответственно, уравнения:
Суммы квадратов отклонений составляют RSS1 = 229, RSS2 = 9804, при этом F = 9804/229 = 42,8. Критическое значение Fкр = 6,39 при 5%-ном (FРАСПОБР(0,05;1;4))[1] уровне значимости. Поскольку F = 42,8 > F кр = 7,7086, то нулевая гипотеза об отсутствии гетероскедастичности отклоняется.
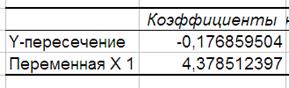
Рис. Г
Рис. Д
Рис. Е
Рис. Ж
На рис. Г-Ж – результаты расчетов в MS Excel.
Тест Глейзера
Тест Глейзера основывается на более общих представлениях о зависимости стандартной ошибки случайного члена от значений объясняющей переменной. Например, зависимость может быть представлена в виде:
si = a + bxig + ei (1.2)
Используя абсолютные значения остатков в качестве оценки si, данная регрессионная зависимость оценивается при различных значениях g и выбирается наилучшая из них.
Таким образом, гетероскедастичность аппроксимируется уравнением:
si = a + bxig,
где si = | ei | – оценка si.
Нулевая гипотеза об отсутствии гетероскедастичности отклоняется, если оценка b значимо отличается от нуля.
Пример 1.3. На основании данных | ei | и x примера 1.1 с использованием различных значений g были оценены уравнения (1.2):
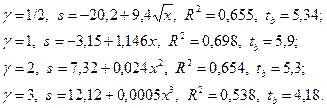
Наилучший результат (по R 2) соответствует значению g =1, при этом оценкой s является величина:
(1.3)
Коэффициент b = 1,146значимо отличается от нуля, следовательно, имеет место гетероскедастичность.