Авторегрессионное преобразование

Пусть исходное уравнение регрессии

(1.4)

содержит автокорреляцию случайных членов.

Допустим, что автокорреляция подчиняется авторегрессионной схеме первого порядка:

,

где r – коэффициент авторегрессии, а u_t – случайный член, удовлетворяющий предпосылкам МНК.

Данная схема оказывается авторегрессионной, поскольку e определяется значениями этой же величины с запаздыванием, и схемой первого порядка, потому что в этом случае запаздывание равно единице.

Величина r есть в точности коэффициент корреляции между двумя соседними ошибками. Пусть r известен.

Обратимся к исходной модели (1.4). Для момента времени t – 1 эта модель примет вид:

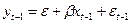(1.5)

Вычтем из обеих частей исходного уравнения (1.4) умноженное на r соотношение (1.5), получим:

Обозначим:

.

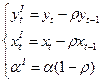Это преобразование переменных называется а вторегрессионным (AR), или преобразованием Бокса-Дженкинса.

Тогда преобразованное уравнение:

,

где t ³ 2, не содержит автокорреляцию, и для оценки её параметров 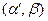используется обычный МНК.

Оценка коэффициента b из этой зависимости непосредственно используется и для исходного уравнения, а коэффициент a рассчитывается по формуле .

На практике величина r  неизвестна, ее оценка получается одновременно с оценками 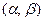в результате следующих итеративных процедур.

Процедура Кохрейна-Оркатта. Процедура включает следующие этапы:

1) применяя МНК к исходному уравнению регрессии, получают первоначальные оценки параметров a, b;

2) вычисляют остатки e и в качестве оценки r используют коэффициент автокорреляции остатков первого порядка, т.е. полагают r = r ₁;

3) применяя МНК к преобразованному уравнению, получают новые оценки параметров a, b.

Процесс обычно заканчивается, когда очередное приближение r  мало отличается от предыдущего. Процедура Кохрейна-Оркатта реализована в большинстве эконометрических компьютерных программ.

Процедура Хильдрата-Лу. Эта процедура, также широко применяемая в регрессионных пакетах, основана на тех же самых принципах, но использует другой алгоритм вычислений:

1. преобразованное уравнение оценивают для каждого значения r из интервала (–1,1) с заданным шагом внутри его;

2. выбирают то значение r, для которого сумма квадратов остатков в преобразованном уравнении минимальна, а коэффициенты регрессии определяют при оценивании преобразованного уравнения с использованием этого значения.

Пример 1.6. Пусть изучается зависимость среднедушевых расходов на конечное потребление y от среднедушевого дохода x по данным (усл. ед.) некоторой страны за 16 лет.

Исходные и расчетные данные представлены в следующей таблице.

			0,18	------	------
			0,76	37,51	38,99	0,44
			0,12	40,99	44,47	-0,42
			0,28	43,45	46,92	0,10
			-1,55	43,92	49,88	-1.77
			-2,58	45,40	51,83	-1.83
			-1,22	50,88	56,30	0,11
			-2,03	47,33	53,75	-1,42
			0,94	54,33	58,24	2,02
			2,10	56,78	61,71	1,73
			3,49	56,74	60,66	2,52
			4,69	57,22	60,65	3,01
			-1,56	57,20	69,14	-3,73
			-1,79	59,70	68,58	-0,79
			-1,01	62,17	70,55	0,12
			-0,82	61,15	69,53	-0,09

Пусть исходная модель имеет вид .

По исходным данным с использованием МНК получено следующее оцененное уравнение регрессии:

(в скобках указаны стандартные ошибки).

Коэффициент автокорреляции остатков первого порядка составляет r = 0,507, следовательно, DW = 2 (1 – r) = 0,986. При уровне значимости 5 % табличное значение d ₁ = 1,10 и d ₂= 1,37. Поскольку 0 < DW < d ₁, то имеется положительная автокорреляция остатков.

Применяя МНК к преобразованным данным

получим оценку преобразованного уравнения:

(в скобках указаны стандартные ошибки).

Коэффициент автокорреляции остатков первого порядка составляет r = 0,145, следовательно, DW = 2(1 – r) = 1,71. Поскольку d ₂ < DW < 4 – d ₂, то автокорреляция остатков отсутствует.

Пересчитывая оценку , получим следующую оценку исходной модели:

Это уравнение отличается от полученного ранее уравнения, оцененного обычным МНК.

[1] F.ОБР.ПХ