Цель работы: формирование системного мышления при обосновании выбора среди альтернативных систем (проектов) по разнонаправленным критериям с применением формальных и неформальных методов.
Последовательность выполнения работы:
1. Формирование исходных данных задачи и её анализ.
2. Определение весовых коэффициентов критериев с привлечением экспертов и оценка качества экспертизы. Допустимый критерий согласованности между экспертами – 0,7; коэффициент конкордации – не ниже 0,85; степень беспорядка во мнениях экспертов – не ниже 0,6.
3. Расчёт приведённых (нормализованных) значений критериев.
4. Расчёт экономической эффективности и выбор наилучшего по данным критериям системы.
5. Провести определение весовых коэффициентов с привлечением большего числа экспертов (или критериев) и рассчитать их значения при полном единодушии экспертов. Оценить качество экспертизы и сравнить с пунктом 1.
6. Увеличить количество систем (или критериев) и повторить пункты 1-3 работы для одного из вариантов. Сделать обоснованные выводы по подготовке решения о выборе наилучшей системы.
Методические рекомендации
Для отладки расчётной схемы и полноты получаемых результатов целесообразно использовать данные простой задачи выбора оптимального проекта различными методами (например, задача 1.16 из [1, с.17]).
Исходные данные: предложены три системы и их расчётные оценки по пяти основным критериям (таблица 4.1). Для выбора лучшей системы (анализа экономической эффективности системы) будем использовать метод приведённых критериев с разнонаправленными весовыми коэффициентами. Пусть оценки по критериям К1, К2, К3, К5 должны быть максимальными, а по К4 – минимальными.
Примечание. При оформлении расчётов необходимо предусмотреть возможность изменения значений параметров в исходной таблице и получения результата без изменения расчётной схемы вычислений.
Таблица 4.1 – Исходные данные
| Системы | Критерии | |||||
| K1 (max) | K2 (max) | K3 (max) | К4 (min) | K5 (max) | ||
| А | 1,1 | 15,3 | 3,6 | 7,3 | ||
| В | 18,3 | 1,1 | 16,5 | 4,8 | 6,8 | |
| С | 20,1 | 1,2 | 17,2 | 3,9 | 9,1 | |
Выполнение лабораторной работы.
1. Выполнение лабораторной работы начинается с оформления шапки отчёта, где в среде Excel указывается сокращённое наименование учебной дисциплины, номер лабораторной работы, фамилия и инициалы студента, дата выполнения работы и номер варианта исходных данных (смотри рисунок 4.1). Далее формируется таблица с исходными данными задачи и выбираются места для промежуточных и окончательных результатов.

Рисунок 4.1 – Исходные данные типовой задачи
2. Для расчёта весовых коэффициентов критериев формируется группа экспертов (например, четыре человека), мнение которых показано в таблице на рисунке 4.2. Используя формулы для расчёта из работы [1], необходимо провести обработку порядковых оценок и получить значения весовых коэффициентов wi.
Величина Ri рассчитывается путем суммирования оценок экспертов по каждому критерию (функция СУММ(), которая вводится в ячейку для расчета R1 и путем автозаполнения переносится в остальные ячейки). Далее, используя функцию МИН(), находим Rmin.
Значение Rmin в формуле вводится с относительной ссылкой на ячейку (т.е. $B$17 – со значками $), т.к. это значение остается неизменным во всех формулах для нахождения Vi.

Рисунок 4.2 - Расчёт весовых коэффициентов
В формулы для расчета Vi и wi вводятся не числа, а ссылки на ячейки, в которых данные числа находятся (например, V1=$B$17/B12, где Rmin находится в ячейке В17). Аналогично вводятся формулы для нахождения wi (рисунок 4.2). Формулы для нахождения Vi и wi вводятся в одну ячейку и путем автозаполнения переносятся в остальные ячейки.
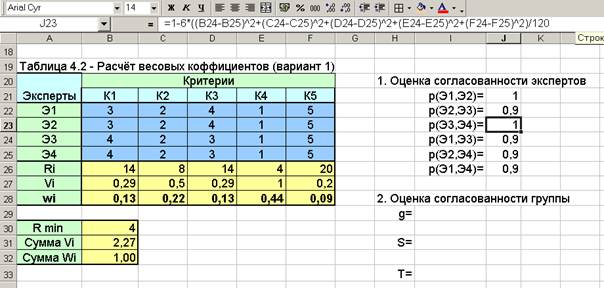
Рисунок 4.3 – Расчет показателя Спирмена
Для оценки качества экспертизы необходимо рассчитать [1]:
а) коэффициент конкордации q=12S/(э2(k3-k)-12эT),
S=Σ(Ri-э(k+1)/2)2, Т=1/12 Σ(t3-t).
б) показатель Спирмена по формуле: ρ(Э1,Э2)=1-(6Σdj2/(k3-k)).
3. Преобразование исходной таблицы данных задачи в таблицу приведённых (нормированных) коэффициентов предполагает пересчет значений максимизируемых критериев К1, К2, К3, К5 по формуле
Нij = (yij-yimin)/(yimax- yimin),
и минимизируемого критерия К4 по формуле Нij = (yimax-yij)/(yimax- yimin).
Результаты пересчета представлены на рисунке 4.4.
4. Аналогично рассчитываются показатели относительной эффективности систем W(j) = Σwi ×Нij.
Вывод: максимальное значение показателя относительного соответствия имеет система С, далее следуют системы A и B.
5. Изменение числа экспертов и критериев задаётся студенту преподавателем. Исходные данные, результаты расчётов и выводы выделяются в новых таблицах.
6. Изменение количество проектов или критериев задаётся студенту преподавателем. Исходные данные, результаты расчётов и выводы выделяются в новых таблицах.
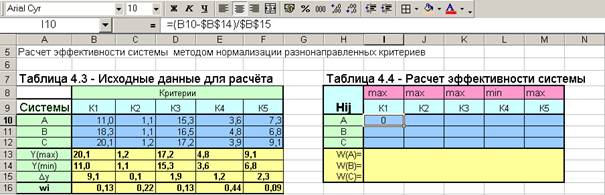

Рисунок 4.4 – Пересчёт коэффициентов (для Н11) и эффективности W(B)
Отчёт представляется в виде файла с выполненными расчётами и пояснительной записки к нему с отражением исходных данных по каждому заданию, особенностей технологии решения задачи и выводов.
Лабораторная работа 5