Цель работы: определение оптимального плана работы организации при ограниченных ресурсах и анализ его изменения при смене параметров внутренней и внешней среды.
Последовательность выполнения работы
1. В табличном редакторе Excel оформить таблицу с исходными данными. Построить систему ограничений и целевую функцию. Определить оптимальный объем выпуска деталей при исходных ограничениях и данных. Провести анализ полноты полученных результатов.
2. Рассчитать три – четыре варианта изменения ресурсов и провести анализ полученных планов работы.
3. Провести анализ изменения плана работы организации при изменении организационной структуры (увеличение числа подразделений) и увеличении числа типов выпускаемых деталей.
4. Рассчитать изменения целевой функции запасов ресурсов на одну единицу, а также верхние и нижние границы устойчивости по ограничениям ресурсов и коэффициентам целевой функции. Определить время окупаемости нового оборудования ценой 1000 рублей, если на одном из участков оно уменьшает загрузку в два раза.
Примечание. При оформлении расчетов предусмотреть возможность изменения значений параметров в исходной таблице и получения результата без изменения расчетной схемы вычислений.
Методические рекомендации
1. Для отладки расчётной схемы и полноты получаемых результатов целесообразно использовать данные простой задачи оптимального распределения ресурсов (например, задача 1.3 из [1].
Исходные данные: На трех участках фирмы обрабатываются два вида деталей. Известна загрузка каждого участка (в процентах) при обработке одной детали и прибыль от реализации одной детали (смотри таблицу 2.1). Необходимо обосновать оптимальный план обработки деталей при полной загрузке участков.
Таблица 2.1 – Исходные данные
| Детали | Загрузка участков, % | Прибыль от продажи одной детали,рубль | ||
| №1 | №2 | №3 | ||
| Д1 | 1,6 | 2,9 | ||
| Д2 | 6,4 | 5,8 | ||
| Макс. загрузка участков |
Выполнение работы начинается с оформления шапки отчёта, где в среде Excel указывается сокращённое наименование учебной дисциплины, номер лабораторной работы, фамилия и инициалы студента, дата выполнения работы и номер варианта исходных данных (смотри рисунок 2.1).
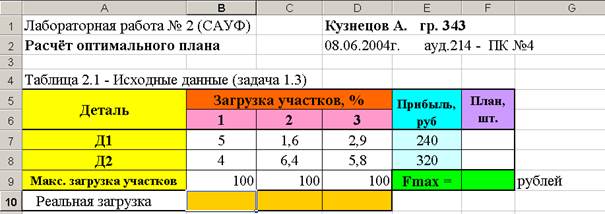
Рисунок 2.1- Пример шапки отчёта, исходных данных и результатов
Для решения задачи надо воспользоваться инструментами Excel:
 Сервис Настройка Поиск решения
Сервис Настройка Поиск решения
и подготовить исходные данные для решения задачи (смотри рисунок 2.2).
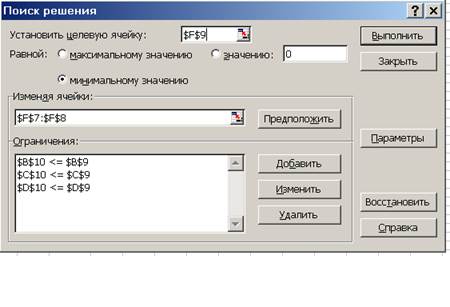
Рисунок 2.2 – Поиск решения
Выполнение расчётов даёт решение задачи (смотри рисунок 2.3).

Рисунок 2.3 – Решение задачи 1.3 [1]
Вывод: оптимальный план работы организации соответствует выпуску деталей в количестве 10 и 12 единиц, при этом прибыль составит 6344,8 рублей и будет недогруз участка №2 на 6 процентов.
2. Для расчёта вариантов распределения ресурсов при изменении исходных данных необходимо повторить таблицу 2.1 с изменением показателей (таблица 2.2), рассчитать новый план работы (смотри рисунок 2.4) и сравнить с начальным вариантом.
Основные изменения ресурсов для индивидуальных заданий приведены в таблице 2.2.
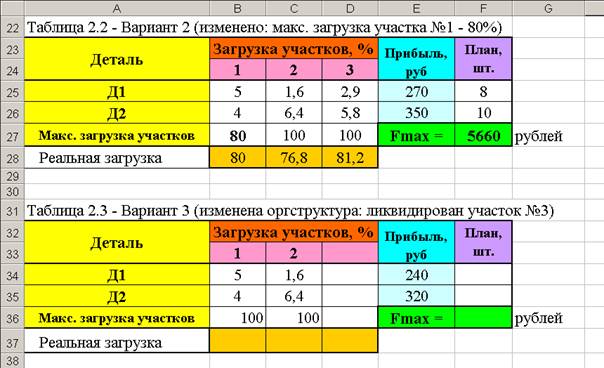
Рисунок 2.4 – Расчёт оптимального плана по вариантам 2 и 3
Таблица 2.2 – Исходные данные для индивидуальных заданий
| Номер задания | Изменённая прибыль по деталям | Изменённая макс. загрузка участков | Изменённая загрузка участков по детали Д1 (Д2) | Изменения оргструктуры и типов деталей | |||||
| Д1 | Д2 | №1 | №2 | №3 | №1 | №2 | №3 | ||
| 3,3 | (7) | Введён участок №4 | |||||||
| - | - | - | - | ||||||
| - | - | - | Добавлена деталь Д3 | ||||||
| - | - | (5) | - | - | |||||
| - | (6) | - | |||||||
| - | - | (3,3) | Введёны участки №4 и №5 | ||||||
| - | - | - | (6) | ||||||
| - | 2,5 | - | - | ||||||
| - | - | - | Введён участок №4 | ||||||
| - | - | - | - | ||||||
| - | - | 2,5 | (6) | Добавлены детали Д3 и Д4 | |||||
| - | - | (3,3) | (6) | ||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | - | 3,3 | (6) | |||||
| - | - | (5) | - | ||||||
| - | - | - | - | (7) | Добавлена деталь Д3 | ||||
| - | - | - | |||||||
| - | 2,5 | Введён участок №4 | |||||||
| - | - | - | - | ||||||
| - | - | - | |||||||
| - | - | (6) | - | Добавлены детали Д3 и Д4 | |||||
| - | - | - | - | (3,3) | |||||
| - | - | - | - | (7) | Введёны участки №4 и №5 | ||||
| - | 2,5 | - | - | ||||||
| - | - | 3,3 | (2) | ||||||
| - | (5) | - | |||||||
| - | - | - | - | - | Введён участок №4 | ||||
| - | - | - | - | ||||||
| - | - | - | - | - | 3,2 | 2 (7) | - |
3. При изменении организационной структуры организации необходимо повторить пункты 1 и 2 для новых исходных данных (например, вариант 3 на рисунке 2.4).
4. Для расчёта изменения целевой функции при изменении запасов ресурсов на одну единицу, а также верхних и нижних границ устойчивости по ограничениям ресурсов и коэффициентам целевой функции необходимо решить двойственную задачу.
Двойственная задача линейного программирования (ЛП) по отношению к основной задаче ЛП удовлетворяет требованиям [3]:
m
S bi yi ® min, yi ³ 0, i=1, 2, …, m,
i=1
m
S aij yi ³ cj, j=1, 2, …, n.
i=1
Каждой переменной исходной задачи соответствует переменная двойственной задачи (и наоборот). Если исходная задача ЛП имеет решение, то имеет решение и двойственная к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.
Значения переменных yi* оптимального решения двойственной задачи называется двойственной оценкой ограничения
n
S aij xj £ bi, j=1, 2, …, n, i=1, 2, …, m.
j=1
Величина yi* показывает, что при увеличении ограничения bi исходной задачи на единицу максимальное значение целевой функции для нового оптимального плана увеличится на yi* единиц.
Нижней границей устойчивости по правой части ограничения (НГпо) называется минимальное значение bi’ правой части основного ограничения, при котором решение y* двойственной задачи не изменится.
Верхней границей устойчивости по правой части ограничения (ВГпо) называется максимальное значение bi’’ правой части основного ограничения, при котором решение y* двойственной задачи не изменится.
Значения НГпо и ВГпо показывают пределы изменения соответствующего ресурса (ограничения в исходной задаче), при котором двойственная оценка этого ресурса не изменится.
Нижней границей устойчивости по коэффициенту целевой функции (НГцф) называется минимальное значение cj’ коэффициента целевой функции основной задачи, при котором оптимальное решение х* исходной задачи не изменится.
Верхней границей устойчивости по коэффициенту целевой функции (ВГцф) называется максимальное значение cj’’ коэффициента целевой функции, при котором оптимальное решение х* исходной задачи не изменится.
Значения НГцф и ВГцф показывают пределы изменения прибыли от продажи единицы соответствующего продукта (детали), при котором количество продукта в оптимальном плане не изменится.

Рисунок 2.5 – Решение исходной и двойственной задач ЛП
Отчёт представляется в виде файла с выполненными расчётами и пояснительной записки к нему с отражением исходных данных по каждому заданию, особенностей технологии решения задачи и выводов.
Особенно важно пояснить содержательную сторону получаемых решений и изменения ресурсов, а также зависимость ресурсов и оптимальных планов при трёх-четырёх однотипных изменениях (для этого допускается использование результатов вычислений другими исполнителями индивидуальных заданий).
Лабораторная работа 3