Построение регрессионных моделей
Цель работы: получить регрессионную модель третьего порядка, используя данные индивидуального задания и проанализировать полученные результаты.
Исходные данные. Для каждого студента преподавателем выдается индивидуальное задание. Оно должно содержать результаты реализованного эксперимента.
Общие положения.
Основные предпосылки применения регрессионного анализа.
В основе обработки результатов активного и пассивного экспериментов с количественными факторами лежит регрессионный анализ, который включает метод отыскания математической модели и статистическую обработку данных эксперимента. Задачами регрессионного анализа являются: получение математической модели процесса; проверка адекватности полученной модели; оценка влияния каждого фактора на процесс.
Предпосылки, при которых может быть использован регрессионный анализ для получения математической модели:
- независимые переменные 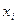 не являются случайными величинами, а задаются исследователем с высокой точностью;
не являются случайными величинами, а задаются исследователем с высокой точностью;
- измеряемые выходные величины 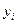 являются независимыми, нормально распределенными случайными величинами;
являются независимыми, нормально распределенными случайными величинами;
- каждая из независимых переменных не является линейной комбинацией остальных независимых переменных;
- интервал между значениями факторов в соседних точках не должен быть меньше или равен ошибке, с которой задается этот интервал;
- значения отклика в точках факторного пространства должны определятся независимо друг от друга;
- в исследуемом интервале варьирования факторов дисперсии воспроизводимости 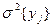 должны быть равны, а их выборочные оценки
должны быть равны, а их выборочные оценки 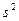
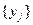 однородны. Проверка оценок дисперсии на однородность проводится по критериям Фишера, Кохрена и Бартлетта.
однородны. Проверка оценок дисперсии на однородность проводится по критериям Фишера, Кохрена и Бартлетта.
Основные виды математических моделей, принимаемых при исследованиях.
Зависимость отклика 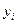 от варьируемых факторов
от варьируемых факторов 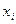 , полученная с применением регрессионного анализа называется регрессионной моделью
, полученная с применением регрессионного анализа называется регрессионной моделью
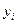 = f (
= f (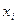 ). (1)
). (1)
Регрессионная модель является частным случаем математической модели объекта. Вид регрессионной модели может быть различным (многочлен определенного порядка, экспонента, тригонометрический многочлен и др.). Обычно он выбирается исследователем до проведения эксперимента. Чтобы оценить применимость построенной модели в планировании эксперимента предусмотрена специальная процедура – проверка адекватности регрессионной модели. Наибольшее применение нашли методы планирования эксперимента, в которых регрессионные модели объектов представляются в виде многочленов первого и второго порядка от варьируемых факторов. В общем случае, при наличии k факторов линейная регрессионная модель объекта имеет вид
y= 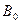 +
+  ∙
∙ 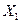 +
+ 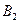 ∙
∙ 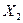 +…+
+…+ 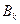 ∙
∙ 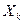 . (2)
. (2)
Коэффициенты регрессии 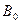 ,
,  ,
, 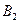 ,…,
,…, 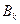 определяются по результатам эксперимента.
определяются по результатам эксперимента.
В случае трех факторов квадратичная регрессионная модель объекта имеет вид
y= 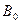 +
+  ∙
∙  +
+ 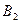 ∙
∙ 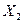 +
+ 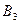 ∙
∙  +
+ 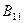 ∙
∙ 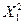 +B22∙
+B22∙ 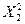 +В33∙
+В33∙ 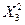 +
+
+ 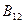 ∙
∙  ∙
∙ 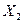 +
+ 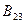 ∙
∙ 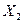 ∙
∙  +
+ 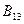 ∙
∙  ∙
∙  . (3)
. (3)
Как видим модель второго порядка (3) включает в себя все слагаемые линейной модели и дополнительно содержит квадратичные члены и члены с парными взаимодействиями.