Рассмотрим идею основного (для количественных факторов) метода обработки результатов эксперимента с целью получения математического описания объекта – метода наименьших квадратов (МНК). Для простоты рассмотрим случай варьирования единственного фактора  . Предположим, что эксперимент состоит в постановке n опытов, и в этих опытах фактор
. Предположим, что эксперимент состоит в постановке n опытов, и в этих опытах фактор  принимает значения
принимает значения  ,
,  ,…,
,…,  . Выходная величина
. Выходная величина 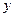 принимает соответственно значения
принимает соответственно значения  ,
,  ,…,
,…,  . Отложим по оси абцисс значения фактора
. Отложим по оси абцисс значения фактора  , принимаемые им в опытах, а по оси ординат – соответствующие значения
, принимаемые им в опытах, а по оси ординат – соответствующие значения 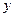 . Получим совокупность точек (рисунок 1).
. Получим совокупность точек (рисунок 1).

Рисунок 1 − Схематическое изображение результатов эксперимента
Найдем величины  ,
,  , …,
, …,  , которые характеризуют отклонение результата эксперимента
, которые характеризуют отклонение результата эксперимента  в точке
в точке  . Согласно МНК оценки для коэффициентов регрессии отыскиваются из условия минимума суммы квадратов отклонений Ф, то есть
. Согласно МНК оценки для коэффициентов регрессии отыскиваются из условия минимума суммы квадратов отклонений Ф, то есть
Ф =  +
+  +…+
+…+  =(
=( -
-  )2+(
)2+( -
-  )2+…+(
)2+…+( -
-  )2=∑(
)2=∑( -
-  )2 èmin.(4)
)2 èmin.(4)
Выполнение этой процедуры дает возможность составить систему нормальных уравнений (СНУ), по количеству равную числу искомых уравнений. В простейшем случае принимаем линейную модель с единственным фактором  , то есть имеющей следующий вид
, то есть имеющей следующий вид
 =
=  +
+  ∙
∙ 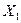 . (5)
. (5)
Подставляя найденные значения  ,
,  ,…,
,…,  в формулу (4), получим для линейной модели
в формулу (4), получим для линейной модели
Ф =( -
-  -
-  ∙
∙  )2+(
)2+( -
-  -
-  ∙
∙  )2+…+(
)2+…+( -
-  -
-  ∙
∙  )2.
)2.
Чтобы найти значения  и
и  , при которых сумма Ф минимальна, возьмем производные от Ф по
, при которых сумма Ф минимальна, возьмем производные от Ф по  и по
и по  и приравняем их нулю:
и приравняем их нулю:
 =-2(
=-2( -
-  -
-  ∙
∙  )-2(
)-2( -
-  -
-  ∙
∙  )-…- 2(
)-…- 2( -
-  -
-  ∙
∙  )=0;
)=0;
 =-2
=-2  (
( -
-  -
-  ∙
∙  )-2
)-2  (
( -
-  -
-  ∙
∙  )-…-2X1n(
)-…-2X1n( -
-  -
-  ∙
∙  )=0.
)=0.
После элементарных преобразований эти уравнения примут вид:
n∙  +
+  (
( +
+  +…+
+…+  )=
)=  +
+  +…+
+…+  ;
;
 ∙(
∙( +
+  +…+
+…+  )+
)+  ∙(
∙( +
+  +…+
+…+  )=
)=  ∙
∙  +
+  ∙
∙  + …+
+ …+  ∙
∙  ,
,
или, сокращая запись,
 ∙
∙  +
+  ∙∑
∙∑  =∑
=∑  ;
;
 ∙∑
∙∑  +
+  ∙∑
∙∑  =∑
=∑  ∙
∙  . (6)
. (6)
Из решения этой системы получим формулы для определения искомых коэффициентов
 =
=  ;
;
 =
=  . (7)
. (7)
Для придания этой системе уравнений более симметричного вида введем фиктивный фактор  , который не имеет физического смысла и в каждом опыте принимает одинаковые значения, равные
, который не имеет физического смысла и в каждом опыте принимает одинаковые значения, равные  =
=  =…=
=…=  =1. Теперь регрессионную модель можно записать следующим образом y=
=1. Теперь регрессионную модель можно записать следующим образом y=  ∙
∙  +
+  ∙
∙  , а систему уравнений соответственно
, а систему уравнений соответственно
 ∙
∙  ∙∑
∙∑ 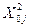 +
+  ∙∑
∙∑  ∙
∙  =∑
=∑  ∙
∙  ;
;
 ∙∑
∙∑  ∙
∙  +
+  ∙∑
∙∑  =∑
=∑  ∙
∙  . (8)
. (8)
Линейная модель (5) справедлива и для среднего арифметического значения
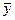 =
=  +
+  ∙
∙  . (9)
. (9)
Вычитая почленно (9) из (5) получим
 -
- 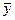 =
=  (
( -
-  ). (10)
). (10)
Коэффициент  для модели (10) можно вычислить по одной из следующих формул:
для модели (10) можно вычислить по одной из следующих формул:
- если n нечетно
 =
=  +
+  +…+(M-1)
+…+(M-1)  ], (11)
], (11)
где M=( +1)/2 и H1=
+1)/2 и H1=  (
( 2-1)/12;
2-1)/12;
- если n четно
 =
=  +
+ 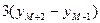 +…+(n-1)
+…+(n-1)  ], (12)
], (12)
где M=  /2 и H1=
/2 и H1=  (
( 2-1)/12.
2-1)/12.
Обратимся теперь к вычислению коэффициентов квадратичной модели с единственным фактором  :
:  =
=  +
+  ∙
∙  +
+  ∙
∙  . (13)
. (13)
Для отыскания трех неизвестных коэффициентов регрессии  ,
,  и
и  надо решить следующую систему из трех линейных уравнений с тремя неизвестными:
надо решить следующую систему из трех линейных уравнений с тремя неизвестными:
 ∙
∙  +
+  ∙
∙  +
+  ∙
∙  =
= 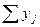 ;
;
 ∙
∙  +
+  ∙
∙  +
+  ∙
∙  =
=  ;
;
 ∙
∙  +
+  ∙
∙  +
+  ∙
∙  =
=  .
.
Аналогично случаю линейной модели, вычисления коэффициентов регрессии значительно упростятся при равноотстоящих значениях фактора  . Математическую модель в этом случае удобно представить в виде
. Математическую модель в этом случае удобно представить в виде
 =
=  (
( )2+
)2+  (
( )+
)+ 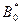 , (14)
, (14)
где h – шаг варьирования фактора  , а коэффициенты
, а коэффициенты  ,
,  и
и  вычисляют по следующим формулам:
вычисляют по следующим формулам:
а) при нечетном n
 =
=  +
+  +…+
+…+  ]-
]-  (
( +
+  + …+
+ …+  )}; (15)
)}; (15)
 =
=  +
+  +…+
+…+  ]; (16)
]; (16)
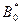 =
= 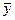 -
- 
 , (17)
, (17)
где H2=  (
( 2-1)(
2-1)( 2-4)/180, M=(
2-4)/180, M=( +1)/2 и H1=
+1)/2 и H1=  (
( 2-1)/12.
2-1)/12.
б) при четном n
 =
=  +
+  +…+
+…+  ]-
]-
-( ) (
) ( +
+  + …+
+ …+  )}; (18)
)}; (18)
 =
=  +
+ 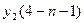 +…+
+…+  ]; (19)
]; (19)
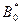 =
= 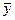 -
- 
 , (20)
, (20)
где M=  /2, H1=
/2, H1=  (
( 2-1)/12 и H2=
2-1)/12 и H2=  (
( 2-1)(
2-1)( 2-4)/180.
2-4)/180.
Пример. В эксперименте получены следующие данные о строительном технологическом процессе, приведенные в таблице 1:
Таблица 1 – Результаты эксперимента

| |||||

| 1,8 | 2,2 | 2,5 | 2,7 | 2,8 |
Опишем эту зависимость уравнением параболы в виде (14). Фактор  варьируется с постоянным шагом h =5. Число опытов n =5 – нечетно, поэтому коэффициенты
варьируется с постоянным шагом h =5. Число опытов n =5 – нечетно, поэтому коэффициенты  ,
,  и
и 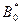 найдем по формулам (15, 16, 17) соответственно.
найдем по формулам (15, 16, 17) соответственно.
Предварительно найдем средние значения варьируемого фактора  и отклика
и отклика  :
:
 =
=  =
=  =15 и
=15 и  =
=  =
=  =2,4.
=2,4.
M=  =
=  =3, H1=
=3, H1=  =
=  =10,
=10,
H2= 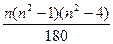 =
=  =14.
=14.
 =
=  +
+  +…+
+…+  ]-
]-  (
( +
+  + …+
+ …+  )}=
)}=
=  +2,2(2-3)2+2,5(3-3)2+2,7(4-3)2+2,8(5-3)2]-
+2,2(2-3)2+2,5(3-3)2+2,7(4-3)2+2,8(5-3)2]-
-  (1.8+2,2+2,5+2,7+2,8)}= -0,05;
(1.8+2,2+2,5+2,7+2,8)}= -0,05;
 =
=  +
+  +…+
+…+  ]=
]=  +2,2(2-3)+
+2,2(2-3)+
+2,5(3-3)+2,7(4-3)+2,8(5-3)]=0,25;
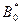 =
= 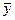 -
- 
 =2,4-
=2,4-  (-0,05)=205.
(-0,05)=205.
Теперь можно записать искомое уравнение регрессии
 =
=  (
( )2+
)2+  (
( )+
)+ 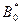 =-0,05(
=-0,05( )2+0,25(
)2+0,25( )+2,5.
)+2,5.
Подставляя значения  для каждого опыта в уравнение регрессии, получим:
для каждого опыта в уравнение регрессии, получим:  =1,8;
=1,8;  =2,2;
=2,2;  =2,5;
=2,5;  =2,7;
=2,7;  =2,8. На графике покажем экспериментальные точки и кривую уравнения регрессии (рисунок 2).
=2,8. На графике покажем экспериментальные точки и кривую уравнения регрессии (рисунок 2).

Рисунок 2 − Схематическое изображение результатов эксперимента
Применение МНК для многофакторных экспериментов
Пусть был поставлен эксперимент, в котором факторы  ,
,  ,…,
,…,  принимали значения
принимали значения  ,
, 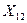 ,…,
,…,  ;
; 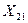 ,
,  ,…,
,…,  ;
;  ,
,  ,…,
,…,  . Перейдем по известным формулам к нормализованным обозначениям факторов и введем в таблицу 2 фиктивный фактор
. Перейдем по известным формулам к нормализованным обозначениям факторов и введем в таблицу 2 фиктивный фактор  и значения отклика.
и значения отклика.
Матрица в таблице 2 при нормализованных обозначениях факторов называется матрицей базисных функций. Она построена по тому же принципу, что и система нормальных уравнений. Каждый ее столбец почленно умноженный на другой столбец и соответствующий коэффициент регрессии представляет собой левую часть системы нормальных уравнений. Запишем систему нормальных уравнений для k факторов:

 ∙
∙  +
+ 
 ∙
∙  +
+ 
 ∙
∙  +…+
+…+ 
 ∙
∙  =
=  ∙
∙  ;
;

 ∙
∙  +
+ 
 ∙
∙  +
+ 
 ∙
∙  +…+
+…+ 
 ∙
∙  =
=  ∙
∙  ;
;

 ∙
∙  +
+ 
 ∙
∙  +
+ 
 ∙
∙  +…+
+…+ 
 ∙
∙  =
=  ∙
∙  ; (21)
; (21)

 ∙
∙  +
+ 
 ∙
∙  +
+ 
 ∙
∙  +…+
+…+ 
 ∙
∙  =
=  ∙
∙  .
.
Таблица 2 − Значения факторов и результатов отклика
| Номер опыта | Значения факторов | Значения отклика | |||||||||
| натуральные обозначения факторов | нормализованные обозначения факторов | из опытов | по уравнению регрессии | ||||||||

| 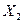
| … | 
| 
| 
| 
| … | 
| 
| 
| |

| 
| … | 
| 
| 
| 
| … | 
| 
| 
| |

| 
| … | 
| 
| 
| 
| … | 
| 
| 
| |

| 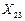
| … | 
| 
| 
| 
| … | 
| 
| 
| |
| . | . | . | … | . | . | . | . | … | . | . | . |
| . | . | . | … | . | . | . | . | … | . | . | . |
| n | 
| 
| … | 
| 
| 
| 
| … | 
| 
| 
|
Математическая модель объекта, записанная в нормализованных обозначениях факторов, позволяет облегчить интерпретацию результатов, так как диапазоны варьирования всех факторов оказываются одинаковыми и равными (-1) и (+1), а все коэффициенты регрессии имеют одинаковую размерность. Это дает возможность оценивать степень влияния факторов по абсолютным значениям коэффициентов регрессии линейной модели.
Пример. По результатам эксперимента получена матрица базисных функций линейной модели. Дополнив ее столбцом фиктивного фактора  и столбцом
и столбцом  (как в таблице 2), приведем ее в таблице 3. Для составления системы нормальных уравнений необходимо вычислить суммы произведений элементов каждой пары столбцов:
(как в таблице 2), приведем ее в таблице 3. Для составления системы нормальных уравнений необходимо вычислить суммы произведений элементов каждой пары столбцов:
 Таблица 3 − Результаты эксперимента и их обработки
Таблица 3 − Результаты эксперимента и их обработки
| Номер опыта | 
| 
| 
| 
| 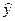
| % расхож дения |
| +1 | -1 | -1 | 8,7 | 3,33 | ||
| +1 | -1 | 5,5 | 5,83 | 6,00 | ||
| +1 | +1 | -1 | 2,95 | 1,66 | ||
| +1 | -1 | +1 | 7,5 | 7,44 | 0,80 | |
| +1 | +1 | 4,2 | 4,57 | 8,81 | ||
| +1 | +1 | +1 | 1,69 | 15,5 |
Теперь система нормальных уравнений, записанная для нормализованных факторов, сводится к виду: 6  =31,2; 4
=31,2; 4  =-11,5; 6
=-11,5; 6  =-3,8, откуда
=-3,8, откуда  =5,2;
=5,2;  =-2,875;
=-2,875; 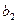 =-0,63. Таким образом, получена следующая линейная модель для нормализованных факторов:
=-0,63. Таким образом, получена следующая линейная модель для нормализованных факторов: 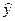 =5,2-2,875
=5,2-2,875  -0,63
-0,63  .
.
Для иллюстрации точности, с которой построенная модель предсказывает результаты эксперимента, подсчитаем значения 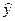 при опытных значениях
при опытных значениях  и
и  и занесем их в столбец 6 таблицы 3. В последнем столбце таблицы 3 приведено в процентах расхождение между экспериментальными результатами и значениями отклика, предсказанными регрессионной моделью. Столь значительные расхождения объясняются тем, что для приведенных экспериментальных данных в таблице 3 нужно использовать полином более высокого порядка для построения математической модели (в этом легко убедиться, если нанести точки будущей зависимости на чертеже).
и занесем их в столбец 6 таблицы 3. В последнем столбце таблицы 3 приведено в процентах расхождение между экспериментальными результатами и значениями отклика, предсказанными регрессионной моделью. Столь значительные расхождения объясняются тем, что для приведенных экспериментальных данных в таблице 3 нужно использовать полином более высокого порядка для построения математической модели (в этом легко убедиться, если нанести точки будущей зависимости на чертеже).