Предварительными исследованиями было установлено, что важнейшими факторами гидролиза древесной массы, влияющими на предел прочности при изгибе ( ,
,  ), являются:
), являются:
- температура ( ,
,  ),
),
- время (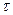 ,
,  ),
),
- кислотность древесной массы ( ,
,  ).
).
Для установления зависимости  от перечисленных факторов была запланирована реализация В-плана
от перечисленных факторов была запланирована реализация В-плана  . Значения уровней факторов и интервалы их варьирования приведены в таблице 4.
. Значения уровней факторов и интервалы их варьирования приведены в таблице 4.
Таблица 4 – Факторы их уровни и интервал варьирования
| Факторы | Уровни факторов | Интервал варьирован. | ||||
| Наименование | Обозначение | нижний | основной | верхний | ||
| натураль-ное | нормализо-ванное | |||||
Температура, 
| 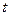
| 
| 20 (-1) | 40 (0) | 60 (+1) | |
Время, 
| 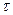
| 
| 0 (-1) | 30 (0) | 60 (+1) | |
Кислотность, 
| 
| 
| 4,5 (-1) | 4,85 (0) | 5,2 (+1) | 0,35 |
Формулы, связывающие нормализованные и натуральные значения факторов, имеют в данном случае вид:
 =(
=(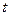 -40)/20,
-40)/20,  =(
=(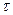 -30)/30,
-30)/30,  =(
=( -4,85)/0,35. (21)
-4,85)/0,35. (21)
Для проверки гипотезы о нормальном распределении выходной величины была поставлена отдельная серия из 50 опытов в условиях: 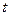 =20
=20  ;
; 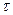 =0
=0  ;
;  =5,2
=5,2  . Нормальность распределения проверялась по критерию
. Нормальность распределения проверялась по критерию  Пирсона. Вычисленное значение
Пирсона. Вычисленное значение  =3,55 оказалось меньше
=3,55 оказалось меньше  , найденного при уровне значимости
, найденного при уровне значимости  =0,05 (
=0,05 ( =5,99). Это позволило принять гипотезу о нормальном распределении выходной величины эксперимента.
=5,99). Это позволило принять гипотезу о нормальном распределении выходной величины эксперимента.
Далее на основании той же серии опытов было рассчитано необходимое число дублированных опытов, которое оказалось равным пяти ( =5).
=5).
Таблица 5 – Значения факторов, результаты опытов и расчетов
| № опыта | Значения факторов | Результаты опытов  , , 
| Результаты расчетов | |||||||||||
| натуральные | нормализованные | |||||||||||||
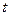 , , 
| 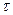 , , 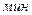
|  , , 
| 
| 
| 
| 
| 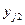
| 
| 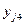
| 
| 
| 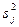
| ||
| 4,5 | -1 | -1 | -1 | 41,5 | 40,5 | 40,2 | 1,330 | |||||||
| 4,5 | +1 | -1 | -1 | 43,5 | 43,5 | 44,2 | 1,075 | |||||||
| 4,5 | -1 | +1 | -1 | 53,5 | 52,7 | 0,450 | ||||||||
| 4,5 | +1 | +1 | -1 | 49,2 | 2,200 | |||||||||
| 5,2 | -1 | -1 | +1 | 34,5 | 32,9 | 2,050 | ||||||||
| 5,2 | +1 | -1 | +1 | 36,5 | 36,5 | 37,4 | 1,175 | |||||||
| 5,2 | -1 | +1 | +1 | 46,5 | 46,5 | 45,2 | 2,075 | |||||||
| 5,2 | +1 | +1 | +1 | 52,5 | 53,5 | 53,5 | 53,5 | 0,875 | ||||||
Матрица В-плана  в нормализованных обозначениях факторов, приведенная в таблице 5, была реализована в ходе эксперимента. В десятом столбце приведены значения отклика, усредненные по дублированным опытам каждой из этих серий
в нормализованных обозначениях факторов, приведенная в таблице 5, была реализована в ходе эксперимента. В десятом столбце приведены значения отклика, усредненные по дублированным опытам каждой из этих серий
 =(
=( )/n; j=1, 2, …, 8; n=1, 2, …, 5.
)/n; j=1, 2, …, 8; n=1, 2, …, 5.
Одиннадцатый столбец содержит результаты расчета дисперсий по каждой серии дублированных опытов
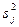 =[
=[  ]/(n-1); j=1, 2, …, 8.
]/(n-1); j=1, 2, …, 8.
Выполним проверку однородности дисперсий опытов. Поскольку в нашем случае имеется равномерное дублирование опытов, то для этого можно использовать критерий Кохрена [1]. Максимальной из дисперсий является дисперсия четвертого опыта  =2,200. Поэтому
=2,200. Поэтому
 =
=  /(
/( )=2,200/11,225=0,196.
)=2,200/11,225=0,196.
Из таблиц Кохрена для  =0,01,
=0,01,  =n-1= 5-1=4 (число степеней свободы каждой выборки), p=8 (количество выборок (j)), находим:
=n-1= 5-1=4 (число степеней свободы каждой выборки), p=8 (количество выборок (j)), находим: 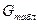 =0,463. Полученное соотношение
=0,463. Полученное соотношение  =0,196 <
=0,196 <  =0,463 позволяет принять гипотезу об однородности дисперсий опытов.
=0,463 позволяет принять гипотезу об однородности дисперсий опытов.
Находим оценку дисперсии воспроизводимости эксперимента как среднее арифметическое дисперсий опытов
 =(
=( )/j=11,225/8=1,403.
)/j=11,225/8=1,403.
Регрессионную модель объекта отыскиваем в виде неполного многочлена третьего порядка, позволяющего учесть наряду с линейными членами все взаимодействия факторов
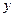 =
=  +
+  ·
·  +
+  ·
·  +
+  ·
·  +
+  ·
·  ·
·  +
+  ·
·  ·
·  +
+ 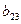 ·
·  ·
·  +
+  ·
·  ·
·  ·
· 
Коэффициенты регрессии вычислим по формулам вида  =(
=( )/j с помощью матрицы базисных функций, приведенной в таблице 5. Для удобства проведения расчетов выполним предварительно некоторые операции в таблице 6 по формулам, указанным в ее шапке.
)/j с помощью матрицы базисных функций, приведенной в таблице 5. Для удобства проведения расчетов выполним предварительно некоторые операции в таблице 6 по формулам, указанным в ее шапке.
Таблица 6 – Значения факторов и результаты расчетов
| № опыта | Факторы | 
| 
|  · · 
|  · · 
|  · · 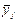
| 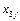 · · 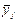
|  · ·  · · 
|  · ·  · · 
| 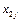 · ·  · · 
|  · · 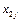 · ·  · · 
| |||

| 
| 
| 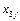
| |||||||||||
| -1 | -1 | -1 | 40,2 | 1,325 | 40,2 | -40,2 | -40,2 | -40,2 | 40,2 | 40,2 | 40,2 | -40,2 | ||
| +1 | -1 | -1 | 44,2 | 1,075 | 44,2 | 44,2 | -44,2 | -44,2 | -44,2 | -44,2 | 44,2 | 44,2 | ||
| -1 | +1 | -1 | 52,7 | 0,45 | 52,7 | -52,7 | 52,7 | -52,7 | -52,7 | 52,7 | -52,7 | 52,7 | ||
| +1 | +1 | -1 | 49,2 | 2,2 | 49,2 | 49,2 | 49,2 | -49,2 | 49,2 | -49,2 | -49,2 | -49,2 | ||
| -1 | -1 | +1 | 32,9 | 2,05 | 32,9 | -32,9 | -32,9 | 32,9 | 32,9 | -32,9 | -32,9 | 32,9 | ||
| +1 | -1 | +1 | 37,4 | 1,175 | 37,4 | 37,4 | -37,4 | 37,4 | -37,4 | 37,4 | -37,4 | -37,4 | ||
| -1 | +1 | +1 | 45,2 | 2,075 | 45,2 | -45,2 | 45,2 | 45,2 | -45,2 | -45,2 | 45,2 | -45,2 | ||
| +1 | +1 | +1 | 53,5 | 0,875 | 53,5 | 53,5 | 53,5 | 53,5 | 53,5 | 53,5 | 53,5 | 53,5 | ||
| Σ | 355,3 | 11,225 | 355,3 | 13,3 | 45,9 | -17,3 | -3,7 | 12,3 | 10,9 | 11,3 |
 =(
=( ·
·  )/j=355,3/8=44,4125;
)/j=355,3/8=44,4125;  =(
=( ·
·  )/j=13,3/8=1,6625;
)/j=13,3/8=1,6625;
 =(
=( ·
·  )/j)=45,9/8=5,7375;
)/j)=45,9/8=5,7375;  =(
=( ·
·  )/j=-17,3/8=-2,1625;
)/j=-17,3/8=-2,1625;
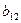 =(
=( ·
·  ·
·  )/j)=-3,7/8=-0,4675;
)/j)=-3,7/8=-0,4675;  =(
=( ·
·  ·
·  )/j=12,3/8=1,5375;
)/j=12,3/8=1,5375;
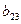 =(
=( ·
·  ·
·  )/j)=10,9/8=1,3625;
)/j)=10,9/8=1,3625;  =(
=( ·
·  ·
·  ·
·  )/j=11,3/8=1,4125.
)/j=11,3/8=1,4125.
Уравнение регрессии в нормализованных обозначениях факторов имеет вид
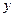 =44,4123+1,6625·
=44,4123+1,6625·  +5,7375·
+5,7375·  -2,1625·
-2,1625·  -0,4625·
-0,4625·  ·
·  +
+
+1,5375·  ·
·  +1,3625·
+1,3625·  ·
·  +1,4125·
+1,4125·  ·
·  ·
·  .
.
Статистический анализ полученного уравнения регрессии начнем с отыскания дисперсий коэффициентов регрессии. Все они одинаковы и равны  =
=  /(n∙j)=1,403/(5∙8)=0,0351.
/(n∙j)=1,403/(5∙8)=0,0351.
Среднеквадратическое отклонение для каждого коэффициента регрессии составляет s(bi)=  =
=  =0,1873.
=0,1873.
Произведем оценку значимости найденных коэффициентов регрессии. Для этого определяем  из таблиц t-распределения Стьюдента при уровне значимости
из таблиц t-распределения Стьюдента при уровне значимости  =0,01 и числе степеней свободы
=0,01 и числе степеней свободы  , связанном с дисперсией воспроизводимости. Поскольку имеет место равномерное дублирование опытов, величину
, связанном с дисперсией воспроизводимости. Поскольку имеет место равномерное дублирование опытов, величину  определяем по формуле
определяем по формуле
 =j·(n-1)=8·(5-1)=32.
=j·(n-1)=8·(5-1)=32.
Из указанных таблиц принимаем  =2,74. Теперь проверим выполнимость соотношения │bi│≤
=2,74. Теперь проверим выполнимость соотношения │bi│≤  ·s(bi)=2,74·0,1873=0,5132.
·s(bi)=2,74·0,1873=0,5132.
Оно выполняется только для коэффициента 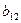 : 0,4675≤0,5132. Поэтому коэффициент
: 0,4675≤0,5132. Поэтому коэффициент 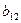 следует признать незначимым и исключить из уравнения регрессии. Все остальные коэффициенты регрессии оказались значимыми и пересчет их не требуется. Регрессионная модель после отбрасывания незначимого члена приняла следующий вид
следует признать незначимым и исключить из уравнения регрессии. Все остальные коэффициенты регрессии оказались значимыми и пересчет их не требуется. Регрессионная модель после отбрасывания незначимого члена приняла следующий вид
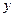 =44,4123+1,6625·
=44,4123+1,6625·  +5,7375·
+5,7375·  -2,1625·
-2,1625·  +
+
+1,5375·  ·
·  +1,3625·
+1,3625·  ·
·  +1,4125·
+1,4125·  ·
·  ·
·  . (22)
. (22)
Определим доверительные интервалы для каждого из значимых коэффициентов регрессии, обозначая истинную величину этого коэффициента через  , по формулам:
, по формулам:
bi- 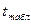 ·s(bi) ≤
·s(bi) ≤  ≤ bi+
≤ bi+ 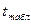 ·s(bi)
·s(bi)
а) для  44,4123-0,5132≤
44,4123-0,5132≤  ≤44,4123+0,5132 43,899≤
≤44,4123+0,5132 43,899≤  ≤44,926;
≤44,926;
б) для  1,6625-0,5132≤
1,6625-0,5132≤  ≤1,6625+0,5132 1,149≤
≤1,6625+0,5132 1,149≤  ≤2,176;
≤2,176;
в) для  5,7375-0,5132≤
5,7375-0,5132≤  ≤5,7375+0,5132 5,224≤
≤5,7375+0,5132 5,224≤  ≤6,251;
≤6,251;
г) для  2,1625-0,5132≤
2,1625-0,5132≤  ≤2,1625+0,5132 2,676≤
≤2,1625+0,5132 2,676≤  ≤1,649;
≤1,649;
д) для  1,5375-0,5132≤
1,5375-0,5132≤  ≤1,5375+0,5132 1,024≤
≤1,5375+0,5132 1,024≤  ≤2,051;
≤2,051;
е) для 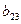 1,3625-0,5132≤
1,3625-0,5132≤  ≤1.3625+0,5132 0,849≤
≤1.3625+0,5132 0,849≤  ≤1,876;
≤1,876;
ж) для  1,4125-0,5132≤
1,4125-0,5132≤  ≤1.4125+0,5132 0,899≤
≤1.4125+0,5132 0,899≤  ≤1,926;
≤1,926;
Проверим теперь адекватность математической модели (22). Дисперсию адекватности  , учитывая дублирование опытов, найдем по формуле
, учитывая дублирование опытов, найдем по формуле
 =
=  =
= 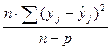 =5∙[(40,2-40,663)2+(44,2-43,738)2+
=5∙[(40,2-40,663)2+(44,2-43,738)2+
+(52,7-52,238)2+(49,2-40,663)2+(32,9-33,353)2+(37,4-36,938)2+
+(45,2-44,738)2+(53,5-53,963)2]/(8-7)=8,556.
где  – число коэффициентов регрессии анализируемой модели,
– число коэффициентов регрессии анализируемой модели,  =7.
=7.
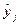 – значение отклика в j-ом опыте, рассчитанное по уравнению (22).
– значение отклика в j-ом опыте, рассчитанное по уравнению (22).
Из таблиц F-критерия Фишера для  =0,01 и числа степеней свободы
=0,01 и числа степеней свободы  =n-p=8-7=1 (числитель) и
=n-p=8-7=1 (числитель) и  =j∙(n-1)=8∙(5-1)=32 (знаменатель) находим
=j∙(n-1)=8∙(5-1)=32 (знаменатель) находим 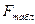 =7,51, а расчетное значение этого критерия найдем по формуле
=7,51, а расчетное значение этого критерия найдем по формуле
 =
=  /
/  =8,556/1,403=6,098.
=8,556/1,403=6,098.
Из сравнения расчетного и табличного значений критериев Фишера  =6,098 <
=6,098 <  =7,51 следует, что гипотеза об адекватности найденной линейной модели (22) подтверждается.
=7,51 следует, что гипотеза об адекватности найденной линейной модели (22) подтверждается.
Для получения регрессионной модели с натуральными обозначениями факторов в уравнение (22) подставим выражения для  ,
,  ,
,  из (21)
из (21)
 =127,46+0,366·
=127,46+0,366· 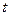 +1,287·
+1,287· 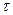 -19,59·
-19,59·  -0,08·
-0,08· 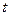 ·
·  -0,206·
-0,206· 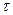 ·
·  +
+
+0,0485· 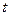 ·
· 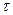 +0,01·
+0,01· 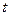 ·
· 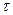 ·
·  . (23)
. (23)
В линейную модель с натуральными обозначениями факторов (23) «вернулся» ранее признанный незначимым коэффициент, учитывающий взаимодействие первого и второго факторов. Очевидно, что с отбрасыванием незначимых коэффициентов не нужно спешить. Не отбрасывая незначимый коэффициент из уравнения, имели бы
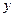 =44,4123+1,6625·
=44,4123+1,6625·  +5,7375·
+5,7375·  -2,1625·
-2,1625·  -0,4625·
-0,4625·  ·
·  +
+
+1,5375·  ·
·  +1,3625·
+1,3625·  ·
·  +1,4125·
+1,4125·  ·
·  ·
·  . (22’)
. (22’)
Тогда, подставляя в регрессионное уравнение (22’) значения нормализованных факторов по формулам (21), получим
 =44,4123+1,6625·(
=44,4123+1,6625·(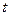 -40)/20+5,7375·(
-40)/20+5,7375·(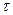 -30)/30-2,1625·(
-30)/30-2,1625·( -4,85)/0,35-
-4,85)/0,35-
-0,4625·(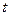 -40)/20·(
-40)/20·(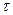 -30)/30+1,5375·(
-30)/30+1,5375·(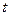 -40)/20·(
-40)/20·( -4,85)/0,35+
-4,85)/0,35+
+1,3625·(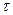 -30)/30·(
-30)/30·( -4,85)/0,35+1,4125·(
-4,85)/0,35+1,4125·(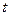 -40)/20·(
-40)/20·(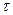 -30)/30·(
-30)/30·( -4,85)/0,35.
-4,85)/0,35.
После элементарных преобразований окончательно получим
 =86,736+0,0196·
=86,736+0,0196· 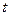 +0,898·
+0,898· 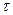 -10,786·
-10,786·  -0,0334·
-0,0334· 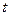 ·
· 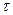 +0,0179·
+0,0179·  ·
·  -
-
-0,1393· 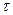 ·
·  -0,00673·
-0,00673· 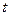 ·
· 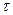 ·
·  . (23’)
. (23’)
Производя подстановку значений факторов, согласно плану эксперимента, в модель (23’) получим результаты, приведенные в таблице 7.
Таблица 7 – Значения отклика из опытов и по уравнениям регрессии
| № опыта | ||||||||

| 40,2 | 44,2 | 52,7 | 49,2 | 32,9 | 37,4 | 45,2 | 53,5 |
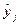 по (23) по (23)
| 40,66 | 43,74 | 52,24 | 49,66 | 33,36 | 36,94 | 44,74 | 53,96 |
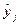 по (23’) по (23’)
| 40,199 | 44,199 | 52,699 | 49,199 | 32,899 | 37,399 | 45,199 | 53,499 |
Наглядное представление о влиянии факторов и их взаимодействий на отклик дает изучение графиков, построенных по уравнению (23).
Проанализируем, например, влияние фактора  и взаимодействия
и взаимодействия  и
и 
 = f(
= f(  ). Для простоты рассмотрим только три прямые из семейства зависимостей.
). Для простоты рассмотрим только три прямые из семейства зависимостей.
I. При  =-1 и
=-1 и  =-1, что соответствует фиксированию факторов
=-1, что соответствует фиксированию факторов  и
и  на нижнем уровне. Подставляя значения
на нижнем уровне. Подставляя значения  =-1 и
=-1 и  =-1 в уравнение (22) получим
=-1 в уравнение (22) получим
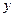 =46,4498+5,7875·
=46,4498+5,7875· 
- при  =-1
=-1 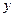 =46,4498+5,7875·(-1)=40,6623;
=46,4498+5,7875·(-1)=40,6623;
- при  =0
=0 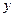 =46,4498+5,7875·(0)=46,4498;
=46,4498+5,7875·(0)=46,4498;
- при  =+1
=+1 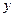 =46,4498+5,7875·(+1)=52,2373.
=46,4498+5,7875·(+1)=52,2373.
По этим значениям 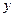 на графике построена прямая 1.
на графике построена прямая 1.
II. При  =0 и
=0 и  =0, что соответствует фиксированию факторов
=0, что соответствует фиксированию факторов  и
и  на основном уровне. Подставляя значения
на основном уровне. Подставляя значения  =0 и
=0 и  =0 в уравнение (22) получим
=0 в уравнение (22) получим
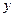 =44,4123+5,7375·
=44,4123+5,7375· 
- при  =-1
=-1 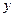 =44,4123+5,7375·(-1)=38,6748;
=44,4123+5,7375·(-1)=38,6748;
- при  =0
=0 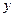 =44,4123+5,7375·(0)=44,4123;
=44,4123+5,7375·(0)=44,4123;
- при  =+1
=+1 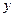 =44,4123+5,7375·(+1)=50,1498.
=44,4123+5,7375·(+1)=50,1498.
По этим значениям 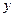 на графике построена прямая 2.
на графике построена прямая 2.
III. При  =+1 и
=+1 и  =+1, что соответствует фиксированию факторов
=+1, что соответствует фиксированию факторов  и
и  на верхнем уровне. Подставляя значения
на верхнем уровне. Подставляя значения  =+1 и
=+1 и  =+1 в уравнение (22) получим
=+1 в уравнение (22) получим
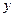 =45,4498+8,5125·
=45,4498+8,5125· 
- при  =-1
=-1 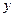 =45,4498+8,5125·(-1)=36,9373;
=45,4498+8,5125·(-1)=36,9373;
- при  =0
=0 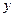 =45,4498+8,5125·(0)=45,4498;
=45,4498+8,5125·(0)=45,4498;
- при  =+1
=+1 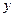 =45,4498+8,5125·(+1)=53,9623.
=45,4498+8,5125·(+1)=53,9623.
По этим значениям 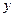 на графике построена прямая 3.
на графике построена прямая 3.
 |
Рисунок 3 − Графики зависимостей отклика от фактора  (
( )
)
Поскольку с ростом фактора  отклик падает (
отклик падает ( <0), то прямая 2 лежит ниже прямой 1, а начало прямой 3 является самым низким значением отклика (при
<0), то прямая 2 лежит ниже прямой 1, а начало прямой 3 является самым низким значением отклика (при  =+1,
=+1,  =-1,
=-1,  =+1). Из-за того, что
=+1). Из-за того, что 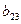 >0 и
>0 и  >0, прямая 3 наклонена под большим углом к оси абсцисс, чем прямые 1 и 2. Отсюда следует, что при большем значении кислотности
>0, прямая 3 наклонена под большим углом к оси абсцисс, чем прямые 1 и 2. Отсюда следует, что при большем значении кислотности  (в большей степени) и температуры
(в большей степени) и температуры 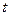 (в меньшей степени) изменение времени гидролиза
(в меньшей степени) изменение времени гидролиза  оказывает более сильное влияние на предел прочности
оказывает более сильное влияние на предел прочности  . Так интерпретируется роль парного взаимодействия факторов
. Так интерпретируется роль парного взаимодействия факторов  и
и  , а также тройного взаимодействия всех факторов.
, а также тройного взаимодействия всех факторов.
Аналогично можно проанализировать влияние на отклик других факторов и их парного или тройного взаимодействия.
Задание. Необходимо проанализировать степень влияния факторов и построить графики зависимостей отклика от каждого фактора при трех сочетаниях уровней варьирования остальных факторов (три графика с тремя прямыми).
Литература
1. ГОСТ Р 56604-2015/ISO/TR 24697:2011. Материалы и изделия текстильные. Руководство по определению прецизионности стандартного метода испытания путем межлабораторных испытаний.
2. Гмурман В.Е. Теория вероятностей и математическая статистика / 11-е изд. стереотипное. – М.: Высшая школа, 2005. – 480 с.
3. Ивченко Г.И. Математическая статистика. Учебное пособие для вузов / Г.И. Ивченко, Ю.И. Медведев. – М.: Высшая школа, 1984. – 248 с.
4. Пижурин А.А. Основы научных исследований в деревообработке. – М.: МГУЛ, 2007. – 305 с.
5. Пижурин А.А. Исследования процессов в деревообработке / А.А. Пижурин, М.С. Розенблит. – М.: «Лесная промышленность», 1984. – 232с.
Викторов Дмитрий Александрович
Методические указания
к контрольной работе
по дисциплине «Основы научных исследований и патентоведения»
для направления подготовки бакалавров 08.03.01 «Строительство»
по профилю «Промышленное и гражданское строительство»
Формат Объём п.л. Тираж экз.
Заказ Бесплатно
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Брянский государственный инженерно-технологический университет»
г. Брянск, пр-т Станке Димитрова 3, редакционно-издательский отдел
Отпечатано: подразделение оперативной печати ФГБОУ ВО «БГИТУ»