Логическая символика и терминология
Для сокращения записей будем использовать логические символы:
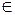– принадлежит,
– содержится,
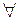– любой, для любого, каждый, для всех и т. п.,
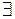– существует, найдется,
: или | – заменяет слова «такой, что…»,
! – единственный,
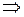– знак следования (в записи 
условие А называется достаточным для В, условие В называется необходимым для А),
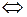– знак равносильности (означает, что и при этом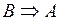 
),
■ – знак окончания доказательства.
Точные грани числовых множеств
Пусть 
.
О. Множество Х называется ограниченным сверху, если
: 
.
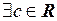Число с называется верхней гранью множества Х.
О. Множество Х называется ограниченным снизу, если
: 
.
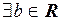Число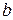 
называется нижней гранью множества Х.
О. Множество Х называется ограниченным, если оно ограничено и сверху, и снизу, т.е.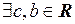 
: 
.
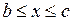Утверждение Множество Х ограничено тогда, и только тогда, когда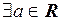 
: 
.
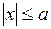О. Максимальным элементом множества Х называется такое число а, что 
: 
.
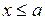О. Минимальным элементом множества Х называется такое число а, что : 
.
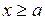О. Множество Х называется не ограниченным сверху, если
: 
: 
.
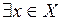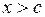О. Множество Х называется не ограниченным снизу, если
: : 
.
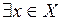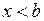О. Множество Х называется неограниченным, если оно не ограничено сверху или не ограничено снизу.
О. Точная верхняя грань – это наименьшая из всех верхних граней, т.е.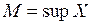 
(супремум), если
1) 
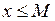; 2) 
.
Или 
.
О. Точная нижняя грань – это наибольшая из всех нижних граней, т.е.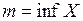 
(инфинум), если
1) 
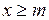; 2)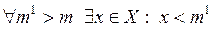 
.
Или 
.
Замечание. 1) Множество может не иметь максимального элемента, но иметь точную верхнюю грань. Например, таково множество 
.
2) Если существует максимальный элемент множества Х, то он совпадает с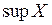 
.
3) Если множество Х не ограничено сверху, то 
, если Х не ограничено снизу, то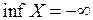 
.
Теорема о существовании точной верхней грани Если множество Х ограничено сверху, то оно имеет, причем единственную, точную верхнюю грань.
Натуральные, рациональные, иррациональные числа
О. Множество М называется индуктивным, если
.
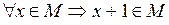О. Множество натуральных чисел – это наименьшее индуктивное множество, содержащее 1. Обозначается N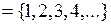 
.
О. Множество целых чисел – это множество
Z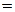 
N 
.
О. Множество рациональных чисел – это множество
Q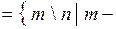 
целое, 
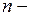натуральное 
.
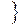Числа, которые не являются рациональными, называются иррациональными.
Любое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби. Например, 
. Иррациональное число – это всегда бесконечная непериодическая десятичная дробь.
2 Числовые последовательности
Определения
Функцией называется правило (закон), по которому каждому элементу множества Х ставится в соответствие единственный элемент множества Y.
Обозначается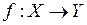 
или 
. Множество Х при этом называется областью определения, а множество Y – областью значений.
Последовательность – это функция, область определения которой есть множество N всех натуральных чисел.
– n- ый член последовательности, 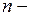номер члена .
Примеры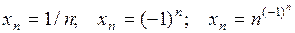 
.
О. Последовательность называется ограниченной сверху, если
: 
.
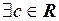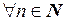
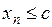О. Последовательность называется ограниченной снизу, если
: 
.
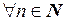
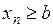О. Последовательность называется ограниченной, если
: 
.
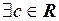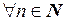
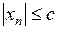О. Последовательность называется возрастающей с номера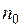 
, если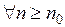 
.
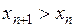О. Последовательность называется убывающей с номера 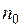, если
.
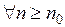
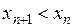Предел последовательности
О. Число а называется пределом последовательности , если
.
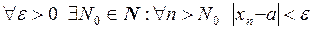Обозначается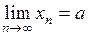 
.
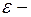окрестностью 
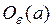точки а называется симметричный интервал 
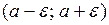. Следующие записи равносильны:
.
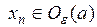
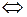
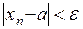
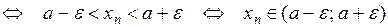Это значит, для любой окрестности точки а существует такой номер 
, что все члены последовательности с номерами, большими, чем этот, принадлежат этой окрестности, т.е.
.
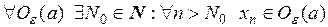Пример 1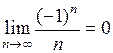 
, так как
(квадратные скобки означают целую часть числа).
Если существует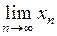 
, то говорят, что последовательность сходится, в противном случае – расходится.
Пример 2 Последовательность 
не имеет предела, так как нет такого числа, в окрестности которого находились бы все члены этой последовательности, начиная с некоторого номера.