О. Функция 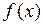 имеет в точке
имеет в точке  локальный максимум, если существует такая окрестность
локальный максимум, если существует такая окрестность 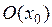 точки
точки  , что
, что
 .
.
О.  – точка строгого локального максимума, если
– точка строгого локального максимума, если
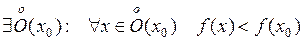 .
.
О. Функция 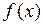 имеет в точке
имеет в точке  локальный минимум, если существует такая окрестность
локальный минимум, если существует такая окрестность 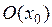 точки
точки  , что
, что
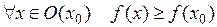 .
.
О.  – точка строгого локального максимума, если
– точка строгого локального максимума, если
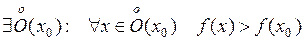 .
.
Локальный максимум и локальный минимум объединяются названием локальный экстремум.
Теорема Ферма
Теорема Ферма Если 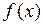 имеет в точке
имеет в точке  локальный экстремум и дифференцируема в этой точке, то
локальный экстремум и дифференцируема в этой точке, то  .
.
Геометрический смысл теоремы Ферма: касательная к графику функции  в точке локального экстремума параллельна оси Ох.
в точке локального экстремума параллельна оси Ох.
Теорема Ролля
Теорема Ролля (о нулях производной) Если 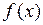 непрерывна на отрезке
непрерывна на отрезке  , принимает в концах этого отрезка равные значения
, принимает в концах этого отрезка равные значения 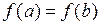 и дифференцируема на интервале
и дифференцируема на интервале 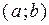 , то существует точка
, то существует точка  , в которой
, в которой 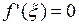 .
.
Геометрический смысл теоремы Ролля: при условиях теоремы Ролля существует точка 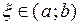 , в которой касательная к графику функции
, в которой касательная к графику функции 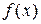 параллельна оси Ох.
параллельна оси Ох.
6.4 Формула Лагранжа конечных приращений.
Теорема Лагранжа Если 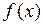 непрерывна на отрезке
непрерывна на отрезке  и дифференцируема на интервале
и дифференцируема на интервале 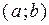 , то существует такая точка
, то существует такая точка  , что
, что  .
.
Геометрический смысл теоремы Лагранжа:  , в которой касательная к графику функции
, в которой касательная к графику функции 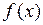 параллельна секущей, соединяющей точки
параллельна секущей, соединяющей точки  и
и 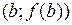 .
.
Следствия 1)Если функция 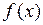 дифференцируема на интервале
дифференцируема на интервале 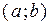 и
и 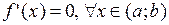 , то
, то  на
на  .
.
2) Если  на
на 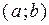 , то
, то 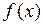 не убывает на
не убывает на 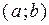 .
.
Если  на
на 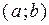 , то
, то 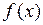 не возрастает на
не возрастает на 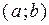 .
.
3) Если две непрерывные функции имеют одинаковые производные, то они отличаются на 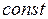 , т.е.
, т.е. 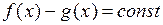 .
.
Правило Лопиталя
Теорема 1 Пусть 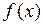 и
и  дифференцируемы на интервале
дифференцируемы на интервале 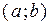 ,
, 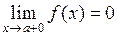 ,
, 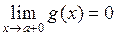 ,
,  и существует конечный или бесконечный
и существует конечный или бесконечный 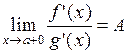 . Тогда
. Тогда 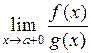 тоже существует и равен А, т.е.
тоже существует и равен А, т.е. 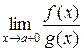
 .
.
Замечание. Утверждение теоремы справедливо и при  , и при
, и при 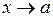 , и при
, и при  .
.
Теорема 2 Пусть 1) 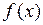 и
и 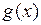 дифференцируемы при
дифференцируемы при 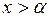 , причем
, причем 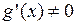 при
при 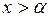 ;
;
2) 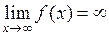 ,
,  ;
;
3) существует конечный 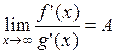 .
.
Тогда существует 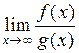
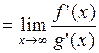 .
.
Замечание. Правило Лопиталя служит для раскрытия неопреде-ленностей вида  и
и 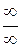 . Иногда к этим неопределенностям удается свести неопределенности
. Иногда к этим неопределенностям удается свести неопределенности 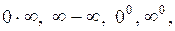
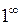 .
.
Исследование функций с помощью производной
Возрастание и убывание функций
Теорема 1 (критерий возрастания дифференцируемой на интервале функции) Для того, чтобы дифференцируемая на интервале 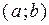 функция
функция  была возрастающей на этом интервале, необходимо и достаточно, чтобы
была возрастающей на этом интервале, необходимо и достаточно, чтобы 
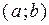 .
.
Теорема 2 (критерий убывания дифференцируемой на интервале функции) Для того, чтобы дифференцируемая на интервале 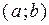 функция
функция  была убывающей на этом интервале, необходимо и достаточно, чтобы
была убывающей на этом интервале, необходимо и достаточно, чтобы 
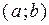 .
.
Теорема 3 (достаточное условие строгого возрастания (убывания) функции) Если 
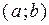
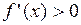 , то
, то 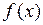 строго возрастает на интервале
строго возрастает на интервале 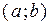 . Если
. Если 
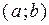
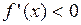 , то
, то 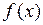 строго убывает на интервале
строго убывает на интервале 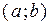 .
.
Теорема 4 Если 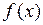 непрерывна на отрезке
непрерывна на отрезке  , дифферен-цируема на интервале
, дифферен-цируема на интервале 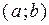 и
и 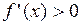 для
для 
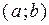 , то
, то 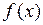 строго возрастает на
строго возрастает на  .
.
Экстремумы функции
О. Точки, в которых  , называются стационарными.
, называются стационарными.
О. Точки, в которых 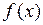 непрерывна, а
непрерывна, а  или не существует, называются критическими
или не существует, называются критическими
Из теоремы Ферма следует, что если 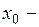 точка экстремума, то
точка экстремума, то  . Поэтому точки экстремума следует искать среди критических точек.
. Поэтому точки экстремума следует искать среди критических точек.
Однако не всякая критическая точка является точкой экстремума. Например, для 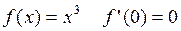 , но
, но 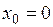 не является точкой экстремума.
не является точкой экстремума.
Теорема (I достаточное условие строгого экстремума) Пусть  дифференцируема в некоторой
дифференцируема в некоторой  и непрерывна в точке
и непрерывна в точке  . Тогда 1) если
. Тогда 1) если 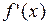 меняет знак с минуса на плюс при переходе через точку
меняет знак с минуса на плюс при переходе через точку  , т.е.
, т.е. 
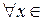
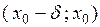
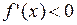 , а
, а 
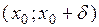
 , то
, то  – точка строгого локального минимума функции
– точка строгого локального минимума функции 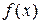 ;
;
2) если 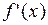 меняет знак с плюса на минус при переходе через точку
меняет знак с плюса на минус при переходе через точку  , то
, то  – точка строгого локального максимума функции
– точка строгого локального максимума функции 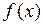 .
.