Из определения предела следует, что любая окрестность предела последовательности содержит все члены этой последовательности, кроме, быть может, конечного числа её членов.
Теорема 1 Числовая последовательность может иметь только один предел.
Теорема 2 Если последовательность сходится, то она ограничена.
Замечание. Обратное не всегда верно. Например, последовательность 
ограничена, но не сходится.
Свойства сходящихся последовательностей, связанные с неравенствами
Теорема 1 (о промежуточной последовательности или теорема о двух милиционерах) Если 
таковы, что
и 
, то 
.
Теорема 2 Если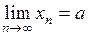 
, 
, причем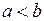 
, то
.
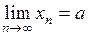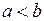Следствие 1 Если и , то 
.
Следствие 2 Если 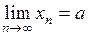, и 
, то 
.
Бесконечно малые последовательности
О. Последовательность называется бесконечно малой, если 
.
Это означает, что 
.
Свойства бесконечно малых последовательностей:
1) сумма конечного числа б.м. последовательностей есть б.м. последовательность;
2) произведение б.м. последовательности на ограниченную последовательность есть б. м. последовательность.
Бесконечно большие последовательности
О. Последовательность называется бесконечно большой, если
.
Пишут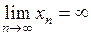 
.
Пусть 
, 
,
.
Тогда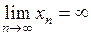 
.
.
.
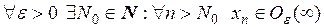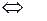
Утверждение 1) любая бесконечно большая последователь-ность является неограниченной (но не любая неограниченная последовательность является б.б. Например, 
);
2) последовательность 
является бесконечно большой тогда, и только тогда, когда последовательность 
является бесконечно малой.
Арифметические операции над сходящимися последовательностями
Утверждение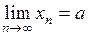 
.
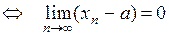Доказательство. Оба утверждения равносильны тому, что
|
|
.■
Теорема Если 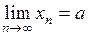, , то
1) 
;
2) 
;
3) если 
и 
, то 
.
Предел монотонной последовательности
Теорема 1 Если последовательность возрастает и ограничена сверху, то она сходится.
Теорема 2 Если последовательность убывает и ограничена снизу, то она сходится.
Некоторые пределы 
, при 
, 
, 
, 
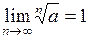2.9 Число e
Рассмотрим последовательность 
. Можно показать, что она возрастает и ограничена сверху.
По теореме о сходимости монотонной последовательности, 
имеет предел. Этот предел обозначается буквой e, т.е.
.
Подпоследовательности. Частичные пределы
Пусть задана последовательность .
О. Рассмотрим строго возрастающую последовательность 
натуральных чисел 
. Тогда последовательность 
называют подпоследовательностью последовательности .
О. Если существует предел подпоследовательности 
, то он называется частичным пределом.
О. Если обозначить 
– множество всех частичных пределов, то 
называется верхним пределом и обозначается 
, 
называется нижним пределом и обозначается 
.
Если не ограничена сверху, то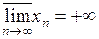 
. Если не ограничена снизу, то 
.
Утверждение 1 Если последовательность имеет предел, то любая её подпоследовательность сходится к тому же пределу.
Утверждение Число а является частичным пределом тогда, и только тогда, когда в любой окрестности точки а содержится бесконечно много членов последовательности. (Доказать)