Графика
Цель настоящего задания - ознакомление слушателей с основными понятиями, элементами сетевых моделей, правилами и техникой построения сетей и методами расчета сетевых графиков. Это позволит применять усвоенную информацию в практической деятельности. Расчет сетевого графика ведется как традиционным способом, так и на ЭВМ. Состав и порядок выполнения задания
1. Построить фрагмент сетевого графика (по индивидуальным
исходным данным - таблица 2 или по данным матрицы неритмичного
потока).
2. Закодировать построенный сетевой график и рассчитать его
табличным методом и методом потенциалов. Нанести на график критический
путь.
3. Привязать сетевой график и календарь и построить его в масштабе
времени.
4. Построить график движения рабочей силы и рассчитать коэффициент
неравномерности изменения численности.
5. Выполнить оптимизацию сетевого графика по рабочим и внести изменения в график движения рабочей силы, если они имеются.
Методические рекомендации к выполнению задания
1. Построить фрагмент сетевого графика.
В основу построения сетевого графика закладываются понятия работы, события и пути.
Работа - любой производственный процесс, требующий затрат времени и ресурсов. Например: устройство фундаментов, монтаж наружных стен здания. Различают действительную работу и ожидание.
Действительная работа - это производственный процесс, требующий затрат времени и ресурсов.
Ожидание - работа, не требующая затрат труда и ресурсов, но требующая затрат времени на технологические и организационные перерывы.
Выделяют также фиктивную работу, обозначают ее пунктирной стрелкой. Фиктивная работа обозначает, что начало последующей работы зависит от окончания одной или нескольких предыдущих.
Путь представляет собой непрерывную последовательность работ от одного события сетевого графика до другого по направлению стрелок.
Длина любого пути определяется суммарной продолжительностью выполнения всех работ, лежащих на нем.
Полным называется такой путь, начало которого совпадает с исходным событием сетевого графика, а конец - с завершающим. Полный путь максимальной продолжительности называется критическим путем. На сетевом графике может быть несколько критических путей.
Приступая к построению сети, необходимо установить номенклатуру работ, выявить работы, которые должны быть завершены ранее, чем начнутся последующие.
Пример построения сетевого графика по матрице неритмичного потока.
| II | ||||
| III | ||||
Матрица рассчитана на основе алгоритма, приведенного в задании I с условием, что второй и третий процессы параллельны и независимы друг от друга.
ВАРИАНТ I. Построение сетевого графика по процессам
Нам известны продолжительность процесса (работы) на каждом объекте, а также начала и окончания работ. Таким образом, последовательно отображая графически выполнения каждого специализированного процесса на каждом объекте и показывая взаимосвязи между процессами, строится сетевая модель (рис.1)
 |
Pис.1 Построение сетевой модели
ВАРИАНТ II. Построение сетевого графика по объектам
 |
Рис.2 Построение сетевого графика по объектам
В данном варианте необходимо показывать на графике все организационные перерывы между процессами на каждом объекте, в противном случае изменятся расчетные показатели общего срока строительства (рис.2).
2. Кодирование построенной сетевой модели и ее расчет
Построенный сетевой график кодируется с таким расчетом, чтобы номер конечного события был больше номера начального события.
Применение методов СПУ - не только знание правил построения сетевых моделей, но и умение рассчитывать их основные параметры:
- продолжительность данной работы;
- раннее начало работы;
- позднее начало работы;
- раннее окончание работы;
- позднее окончание работы;
- общий (полный) резерв времени;
- частный резерв времени;
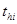- продолжительность предшествующей работы;
- продолжительность последующей работы.
В случае построения графика по данным матрицы неритмичного потока необходимо сопоставить критический путь на сетевом графике с безразрывным путем на матрице.
Для осуществления расчета необходимо знать продолжительность каждой работы. Если сетевой график строится по вариантам матрицы неритмичного потока, то продолжительность соответствует продолжительностям процессов при поточном строительстве.
В случае построения сетевого графика по приведенным в задании
индивидуальным исходным данным (табл.2), где указана трудоемкость каждой работы, студенту необходимо, исходя из трудоемкости, определить продолжительность работы и количество рабочих, ее выполняющих.
Сетевой график рассчитать табличным методом и методом потенциалов. Сопоставить полученные результаты.
Таблица 1
Расчет сетевого графика
| Код работы | Продолжительность | RN | RО | РN | РО | R | R |
| 1-2 | |||||||
| 1-3 | |||||||
| 2-3 | |||||||
| 2-5 | |||||||
| 3-4 | |||||||
| 4-5 | |||||||
| 4-6 | |||||||
| 5-6 |
RN, RО - раннее начало и раннее окончание работ соответственно. РN РО - позднее начало и позднее окончание работ.
R - общие резервы.
r - частные резервы.
4. Привязка сетевого графика к календарю и построение его в
масштабе времени
Для привязки графика к календарю строится шкала времени, состоящая из двух полос. В верхней полосе проставляется рабочее время, согласно расчету от 0 до Ткр. В нижней полосе - календарное время за вычетом субботних, воскресных и праздничных дней.
За начало строительства может быть принята любая дата, от которой и ведется исчисление календарного времени.
Затем сетевой график привязывают к шкале времени по ранним началам. Стрелки графика могут быть горизонтальные, наклонные и ломаные, но во всех случаях их проекция на шкалу времени должна соответствовать заданной продолжительности этих работ. Частные резервы показываются пунктиром, и их величина также определяется по шкале времени.
5. Построение графика движения рабочих и его оптимизация
Этот график также строится на шкале времени. На сетевом графике рядом с продолжительностью каждой работы в скобках проставляется количество рабочих, занятых на выполнении работы, которое указано в индивидуальном задании. Затем строится вспомогательный график. В масштабе времени горизонтальными линиями вычерчивается каждая работа с ее резервом (пунктирная линия).
После построения вспомогательного графика подсчитывается численность рабочих за каждый день. Вертикальный масштаб (число рабочих) принимается студентом произвольно. На основе полученных данных строится график изменения количества рабочих по дням. При наличии на нем пик и впадины определяют максимальное число рабочих, занятых в один день (Rmах). Затем рассчитывается среднее число рабочих за весь период строительства (Rcр).
Rcр= 
где А - суммарная трудоемкость в чел. днях всех работ графика;
Т - продолжительность ведения работ (величина критического пути). Коэффициент неравномерности изменения численности рабочих (К) определяется следующим образом:
R ср = , к = 
К - не должен превышать 1.8. Если К >1.8, то график движения рабочей силы следует оптимизировать путем замедления некоторых процессов и уменьшения количества рабочих, но при неизменной трудоемкости, что дает возможность уменьшить Rmax, а, следовательно уменьшить коэффициент неравномерности изменения численности рабочих.
Таблица 2
Варианты исходных данных для 2-го задания
| № вар. | Кол-во событий | Кол-во работ | Из них фиктив. | Трудоемкость работ | |||||
| 6,4,16,9,12,3,6,4,7,3,12,30,6,4,3,30, 16, 3 | |||||||||
| 6,20,14,6,3,2,18,9,10,8,12,15,6,12. | |||||||||
| 6,8,16,16,6,6,3,15,1,15,4,4,12,10,3,145. | |||||||||
| . | 4,12 18,6,21,2,6,14,18,32,8,10,18,8,1, 2. | ||||||||
| 2,4,4,3,1,12,3,4,18,16,15,16,15,14,12. | |||||||||
| 6,12,32,44,30,21,40,54,12,15,30,18,32,12, 16,14,25,24,45,18,24,51,63. | |||||||||
| 18,4,3,21,25,40,32,6,12,15,22,14, 12,26,33,51,6,12,14,5,8,21. | |||||||||
| 8,14,4,6,24,32,33,12,18,21,44,52, 18,72,3,20,30,16,10,11,33,40. | |||||||||
| 25,45,18,9,17,14,72,16,51,63,11,18, 44,46,13,15,4,6,2,40,1,14,20. | |||||||||
| 12,32,2,10,42,4,63,60,72,30,26,14, 15,20,11,33,40,51,18,4,21,18. | |||||||||
| 2,18,4,10,32,41,32,35,17,14,33,42, 18,4,2,10,12,3,2,21. | |||||||||
| 10,32,17,12,4,3,1,22,18,30,42,13,25 11,14,32,20,14,18,30,51,15,30,25. | |||||||||
| 14,18,32,41,60,72,14,32,18,17,4,60, 13,42,33,12. | |||||||||
| 4,6,21,12,18,2,18,12,10,15,30,14, 25,45,14,18,24,31,63. | |||||||||
| . | 2,4,3,4,1,13,12,40,21,18,42,50,13, 44,25,17,11,9,7,6,13,12,14. | ||||||||
| 18,4,25,40,6,32,16,22,6,12,6,12,14,5,8,21. | |||||||||
ЗАДАНИЕ 3
Методы построения и расчета сетевых циклограмм
При разработке календарных планов строительства отдельных объектов и комплексов широкое распространение получили сетевые графики.
Преимущества сетевых методов планирования и управления общеизвестны. Однако в условиях поточной организации строительства традиционные методы построения и расчета сетевых графиков не достаточно эффективны. Сетевые графики, разработанные без учета основных требований теории строительного потока, искажают целый ряд показателей календарного плана, что позволяет принимать желаемые результаты за действительные.
С другой стороны, методы построения и расчета циклограмм поточного строительства также имеют ряд недостатков, к числу которых в первую очередь надо отнести упрощение схем взаимосвязи работ. Попытки перенесения основных требований строительного потока на сетевой график чреваты ошибками двух типов.
Введение в топологию сетевого графика требования непрерывности работы бригад и звеньев приводит к ложным связям, когда начало работ на некоторых захватках зависит от окончания предыдущих работ на последующих захватках. Чтобы не допустить таких ошибок, в сетевой график обычно вводят дополнительные события и связи. Однако при расчете таких графиков традиционными способами появляются скрытые простои бригад при переходе с одной захватки на другую.
Предлагавшиеся в различное время методы отображения принципов и потока в сетевых графиках сводятся в основном к предварительному расчету параметров циклограммы с последующим введением этих параметров в сетевую модель. Такой подход также не лишен недостатков. Матричный расчет параметров циклограммы основан на простой форме взаимной зависимости работ. Расчет циклограммы со сложной взаимосвязью процессов является чрезвычайно громоздким и по существу сводит на нет все преимущества сетевых методов. Выйти из этого порочного круга можно только с помощью синтеза идей сетевого планирования и теории строительного потока.
Наиболее удобной и компактной для отображения взаимосвязи работ в сетевой циклограмме является сетевая модель, ориентированная на события. В такой модели работы обозначаются кружочками, а связи - стрелками. Выбор этой топологии обусловлен еще и тем, что по структуре она максимально приближена к матрице процессов.
Это обстоятельство позволяет непосредственно на сети использовать принцип расчета сближений смежных потоков.
Рассмотрим топологию сетевой циклограммы с простой формой взаимосвязи работ (рис. 1.).
Естественно, что простой тип взаимозависимости процессов является в большинстве случаев весьма условным. Реальная технология и организация строительства характеризуются более сложной взаимосвязью работ, когда процессы могут выполняться параллельно и независимо друг от друга, и возможность начала одной работы определяется окончанием выполнения двух и более работ, (рис. 2).
Основные параметры сетевых циклограмм, характеризующие развитие процессов в пространстве и времени: продолжительность выполнения работ на захватках, время начала и окончания, организационные перерывы между окончанием предыдущего и началом последующего процесса на каждой захватке и резервы времени.
Следует отметить, что резервы времени выполнения работ в сетевой циклограмме носят специфический характер, связанный с требованием непрерывной занятости рабочих в потоке. Очевидно, что нарушение сроков выполнения любой работы приводит к сдвигу раннего начала последующих. В сетевой циклограмме имеют место лишь общие резервы времени, которые в дальнейшем будем называть просто резервами времени.
Работы сетевой циклограммы, не имеющие резервов времени, являются критическими. Заметим, что работы последнего в потоке процесса всегда критические, поскольку нарушение сроков их выполнения всегда приводит к увеличению общей продолжительности потока.
Расчет параметров сетевой циклограммы состоит из следующих этапов:
1. Начало первого процесса в потоке принимается за "О", тогда окончание
этого процесса на первой захвате будет 
= 
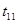. Начало первого процесса на второй захвате равно его окончанию на первой захвате и т. д.
В общем случае:
2. Начало каждого последующего процесса в потоке, т. е. на первой
захвате, определяется как окончание предыдущего процесса на первой
захвате плюс организационный перерыв:
3. Организационные перерывы между каждой парой процессов на соответствующих захватках определяются после расчета начала и окончания лих процессов на всех остальных захватках:
4. Резерв времени любой работы определяется как минимум среди
организационных перерывов:
5. Если начало процесса зависит от двух и более работ, то:
6. Резервы времени работ, от которых зависят несколько процессов,
определяются следующим образом:
,
где jе - номера последующих процессов, которые зависят от данного. Примеры расчетов приведены на рис. 1 - 2.
|
Рис.1 Топология сетевой циклограммы с простой формой взаимосвязи работ
|
Рис.2 Топология сетевой циклограммы со сложной формой взаимосвязи работ