Решение задачи определения оптимальной очередности строительства объектов может дать значительный экономический эффект за счет сокращения общего срока строительства без привлечения дополнительных ресурсов. Определение оптимального порядка включения объектов в поток путем прямого перебора различных вариантов весьма затруднительно, поскольку общее их число составляет n!, где n - количество объектов.
Математический аппарат, позволяющий находить абсолютно оптимальный вариант строительства объектов, на сегодняшний день не разработан. В связи с этим нами предлагается ряд эвристических методов решения этой задачи, позволяющих при сравнительно небольших затратах времени получать решения, достаточно близкие к оптимальному. Ниже предлагается один из таких алгоритмов, основанный на направленном переборе и оценке вариантов.
Алгоритм
Постановку задачи в общем случае можно сформулировать следующим образом. Даны n объектов, по которым известны продолжительности выполнения основных строительно-монтажных работ t 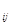 , где i- порядковый номер объекта, j-номер работы. При этом предполагается, что число рабочих в каждой бригаде, выполняющей определенный вид работы, являются постоянным. Требуется определить такую очередность строительства объектов в потоке, при которой общая продолжительность объектного потока была бы минимальной.
, где i- порядковый номер объекта, j-номер работы. При этом предполагается, что число рабочих в каждой бригаде, выполняющей определенный вид работы, являются постоянным. Требуется определить такую очередность строительства объектов в потоке, при которой общая продолжительность объектного потока была бы минимальной.
Решение задачи состоит из ряда этапов.
1. Фиксируется произвольная исходная очередность возведения объектов и определяется общая продолжительность строительства при этой очередности:
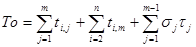 , 1.6
, 1.6
где
τj = 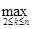
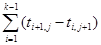 ; 1.7
; 1.7
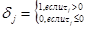
Символ δj означает, что суммируются только положительные значения
2. Определяются все возможные комбинации попарного возведения
объектов в очередности i—>к (i 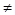 k). Очевидно, что общее количество таких
k). Очевидно, что общее количество таких
комбинаций будет равно n (n-1).
3. Рассчитываются показатели продолжительности цикла для каждой
пары объектов при очередности i —> k и k -> i.
Продолжительность возведения пары объектов в очередности i —> k определяется по формуле
| 1..8. |
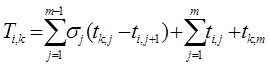
То же при очередности k 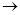 i:
i:
| 1.9 |
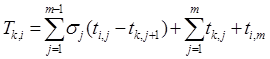
В формулах 1.8 и 1.9 последние две составляющие означают, соответственно, продолжительность выполнения всех процессов на первом объекте и продолжительность последнего процесса на втором объекте.
4. Строится вспомогательная матрица, размерностью n х n
Элементами этой матрицы являются числа 0 и 1. При этом, если Т  < T
< T 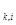 , то на пересечение строки 1 и столбца 1с заносится 1, а на пересечение строки k и столбца i - 0. В случае Т
, то на пересечение строки 1 и столбца 1с заносится 1, а на пересечение строки k и столбца i - 0. В случае Т  = T
= T 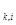 , в обе клетки заносится 1.
, в обе клетки заносится 1.
5. На основе вспомогательной матрицы строятся все полные
допустимые последовательности объектов.
Последовательность объектов i 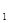 , i
, i 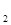 ,…, i
,…, i 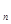 называет допустимой, если для любой пары смежных объектов i
называет допустимой, если для любой пары смежных объектов i  i
i  элемент вспомогательной матрицы в клетке (k, 1) равен 1. Таким образом, переход с объекта к на объект 1 разрешается, если Т
элемент вспомогательной матрицы в клетке (k, 1) равен 1. Таким образом, переход с объекта к на объект 1 разрешается, если Т 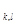 < Т
< Т 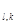 . Последовательность объектов является полной, если она содержит все n объектов без повторений.
. Последовательность объектов является полной, если она содержит все n объектов без повторений.
Полные допустимые последовательности объектов строятся путем последовательного "считывания" вспомогательной матрицы.
6. Среди всех полных допустимых последовательностей объектов
выбирается последовательность, соответствующая минимальной общей
продолжительности строительства.
ПРИМЕР. Рассмотрим алгоритм решения задачи на методическом примере. Заданы четыре объекта, возводимые одним объектным потоком. Исходные данные представлены в табл. 4.
Таблица 4
Матрица исходных данных
| i/j | 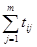
| ||||
Общая продолжительность строительства при исходной очередности 1-2-3-4 согласно 1.6 составит То= 21+16+6=43
Количество вариантов попарного возведения объектов (т.е. объекта i за объектом к, i 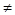 k) равно n*(n-1) =4*3=12.
k) равно n*(n-1) =4*3=12.
Рассчитаем показатели продолжительности цикла для каждой пары объектов при очередности i —>k и k —> i по формулам 1.8 и 1.9. Расчеты производятся непосредственно на матрице исходных данных.
Т 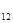 =2+21+2=25
=2+21+2=25
Т 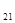 =9+14+3=26
=9+14+3=26
Т 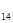 =1+21+6=28
=1+21+6=28
Т 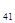 =6+16+3=25
=6+16+3=25
Т 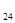 =3+14+6=23
=3+14+6=23
Т 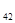 =2+6+2=20
=2+6+2=20
Т 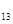 =3+21+8=32
=3+21+8=32
Т 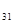 =3+19+3=25
=3+19+3=25
Т 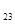 =4+14+8=26
=4+14+8=26
Т 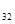 =1+19+2=22
=1+19+2=22
Т 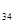 =1+19+6=26
=1+19+6=26
Т 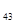 =0+16+8=24
=0+16+8=24
Результаты расчетов используем для построения вспомогательной матрицы (табл. 5)
Таблица 5
Вспомогательная матрица
Поскольку Т 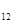 < Т
< Т 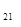 , то в клетку (1,2) заносится 1.
, то в клетку (1,2) заносится 1.
Клетки (1,3) и (1,4) заполняются нулями, так как Т 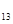 > Т
> Т 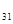 и Т
и Т 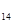 >Т
>Т 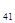 .
.
Все элементы второй строки матрицы равны 0, так как Т 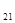 > Т
> Т 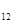 , Т
, Т 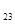 >Т
>Т 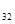 и Т
и Т 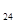 >Т
>Т  .Аналогично заполняются третья и четвертая строки матрицы.
.Аналогично заполняются третья и четвертая строки матрицы.
Полные допустимые последовательности объектов строятся путем построчного считывания вспомогательной матрицы, начиная с каждого из четырех объектов.
Сначала пытаемся построить такую последовательность, которая начинается с первого объекта. Просмотр первой строки матрицы показывает, что с первого объекта можно перейти на второй объект, так как остальные показатели первой строки равны 0. Таким образом, ни одной допустимой последовательности объектов, начинающейся с первого объекта, в данном случае не существует. Аналогичный результат получается и при попытке построить такую последовательность, начиная со второго объекта.