Переход в уравнении Дирака к шредингеровской волновой функции
Для расчета релятивистских поправок к энергиям уровней атома водорода, рассчитанных в рамках классической квантовой механики, удобно использовать приближенную форму уравнения Дирака, получающуюся в результате разложения релятивистски инвариантного уравнения по степеням 1/с.
Обратный переход от четырехкомпонентной волновой функции к "Шредингеровско подобной" может быть осуществлен за счет перенормировки компоненты-столбца Y+, в ходе которой необходимо сохранить только слагаемые, дающие в окончательном ответе слагаемые, порядок которых не меньше, чем 1/c2. Для этого в исходном уравнении Дирака (13.27) должны быть опущены все слагаемые, содержащие векторный потенциал (14.1). Для выделения главной части волновой функции удобно исключить энергию покоя из фазового множителя одной из компонент волновой функции (14.2). При соответствующем выборе фазового множителя отвечающая антисимметричной линейной комбинации волновая функция оказывается существенно меньшей, чем симметричная комбинация и при этом весьма просто выражается через нее (14.3).
· Малость антисимметричной компоненты позволяет рассматривать только симметричную часть волновой функции, перенормировав ее таким образом, чтобы при этом с выбранной точностью был учтен вклад антисимметричной части (14.4). В результате оказывается, что в качестве решения уравнения Дирака можно использовать волновую функцию "стандартного Шрегиндеровского вида".

| (14.1) | Приближенная запись уравнений Дирака, в которой опущены слагаемые с векторным потенциалом. |
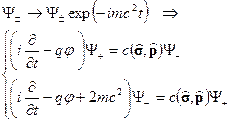
| (14.2) | Фазовое преобразование дираковских волновых функций. |

| (14.3) | Приближенное выражение для малой антисимметричной добавки. |

| (14.4) | Условие нормировки дираковской волновой функции и ее приближенного разложения.. |

| (14.5) | Окончательное правило перенормировки дираковских волновых функций для представления их в шредингеровской форме. |
14.2. Разложение уравнения Дирака по степеням a=1/с
Уравнение Дирака может быть представлено в форме, сходной со стандартным уравнением Шредингера, если все входящие в систему (14.2) слагаемые разложить по степеням a (14.6-14.7) и перейти в соответствии с ранее полученным соотношением (14.5) к шредингеровской волновой функции (14.8 - 14.9). Использование достаточно простых операторных тождеств (14.10) позволяет получить окончательное выражение для релятивистского гамильтониана для электрона в атоме.(14.11). Послднее отличается от классического тремя слагаемыми, выяснению физического смысла которых посвящен следующий пункт.

| (14.6) | Приближенное представление антисимметричной компоненты волновой функции. |


| (14.7) | Результат подстановки (14.6) в уравнение для симметричной компоненты. |

| (14.8) | Результат замены симметричной компоненты волновой функции на шредингеровскую в соответствии с соотношением (14.5). |

| (14.9) | Следствие уравнения (14.8). |


| (14.10) | Операторные тождества. |

| (14.11) | Окончательное выражение для релятивистского гамильтониана. |
Физический смысл дополнительных слагаемых
Выяснение "физического смысла" выражений, возникающих как следствие носящего наиболее фундаментальный характер уравнения Дирака, по-видимому, состоит в получении их классических аналогов. Так первая поправка к оператору Гамильтона (14.11) соответствует учету наличия зависимости релятивистской массы частицы от скорости, о чем свидетельствует полное сходство оператора с третьим слагаемым разложения в ряд Тейлора классического выражения для релятивистской энергии (14.12).
Для выяснения физического смысла второго поправочного слагаемого достаточно рассчитать классическое выражение для добавки к энергии атома за счет взаимодействия обусловленного спином магнитного момента электрона с магнитным полем, создаваемым движущимся относительно электрона положительно заряженным ядром (14.13). Указанное взаимодействие носит название спин-орбитального и играет доминирующую роль в формировании тонкой структуры спектральных линий. Получаемое из классических соображений выражение оказывается полностью соответствующим добавке к оператору Гамильтона (14.14), если в качестве гиромагнитного отношения в случае спина использовать классическое выражение, получаемое для магнитного момента равномерно заряженного по объему вращающегося сферического тела. Следует повторно напомнить о том, что в задаче о поведении электрона во внешнем магнитном поле спиновое гиромагнитное отношение оказывалось в два раза большим по сравнению с классическим выражением.
Что же касается последнего слагаемого, то оно в соответствии с уравнением Пуассона оказывается отличным от нуля только для s-состояний электрона в атоме. Это слагаемое компенсирует расходимости, возникающие в выражении для спин-орбитального взаимодействия в случае его применения к вычислению энергий s-состояний атома.

| (14.12) | Релятивистское выражение для кинетической энергии тела, "объясняющее" смысл первой поправки к классическому гамильтониану. |

| (14.13) | Классическое выражение для добавочной энергии взаимодействия спинового магнитного момента электрона с магнитным полем, создаваемым эффективным движением ядра. |
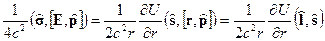
| (14.14) | Оператор поправки к энергии за счет спин-орбитального взаимодействия. |