Содержание
1. Составление дифференциального уравнения движения механической системы
2. Определение реакций внешних и внутренних связей
3. Определение закона движения системы
4. Результаты расчетов
5. Анализ результатов вычислений
6. Результаты анализа
Выводы
Цели и задачи
Наличие упругих связей в механической системе в сочетании с внешним периодическим воздействием может привести к дополнительным колебательным движениям ее элементов. Поэтому теория колебаний и, в частности, раздел, посвященный малым линейным колебаниям, имеет много важных приложений в различных областях науки и техники.
Выделение линейных моделей в особый класс вызывается рядом причин:
• с помощью линейных моделей исследуется широкий круг явлений, происходящих в различных механических системах;
• интегрирование линейных дифференциальных уравнений с постоянными коэффициентами является, с математической точки зрения, элементарной задачей.
Поэтому инженер–исследователь стремится по возможности описать поведение системы с помощью линейной модели для облегчения процедуры анализа ее движения.
При проектировании механических систем обычно используют критические режимы внешних воздействий на них. В этом случае внешние факторы:  – коэффициент демпфирования,
– коэффициент демпфирования,  – амплитуда и частота возмущающей силы, изменяются незначительно. Конструктивные параметры механических систем (их геометрические размеры) определяются условиями их функционирования и, следовательно, могут изменяться в очень узком диапазоне. Актуальной становится такая задача исследования механической системы, при которой могут изменяться массовые параметры системы и жесткость упругого элемента.
– амплитуда и частота возмущающей силы, изменяются незначительно. Конструктивные параметры механических систем (их геометрические размеры) определяются условиями их функционирования и, следовательно, могут изменяться в очень узком диапазоне. Актуальной становится такая задача исследования механической системы, при которой могут изменяться массовые параметры системы и жесткость упругого элемента.
Поэтому целью курсовой работы является исследование и анализ динамического поведения механической системы с упругими связями с помощью основных теорем и принципов теоретической механики.
Для достижения этой цели, необходимо решить поставленные задачи:
1. составить дифференциальное уравнение движения системы;
2. сформировать систему уравнений для определения динамических реакций внешних и внутренних связей;
3. Найти закон движения системы, т. е. проинтегрировать дифференциальное уравнение движения при заданных начальных условиях;
4. провести численный анализ полученного решения с использованием ЭВМ.
Груз 1 один подвешен на нити к центру невесомого блока 2. Меньшая ступень блока 2 прикреплена нитью к горизонтальной поверхности, а нить, намотанная на большую ступень – навита на закрепленный в центре блок 3. Далее нить с блока 3 наматывается на меньшую ступень катка 4, который катится по шероховатой горизонтальной поверхности, касаясь ее большей ступенью. Центр катка связан с пружиной, другой конец которой закреплен неподвижно. Нити и пружина, которые являются невесомыми, параллельны соответствующим плоскостям. Нити являются нерастяжимыми и абсолютно гибкими. Сопротивление, возникающее в подшипниках блока, пропорционально первой степени угловой скорости блока: 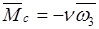 . Качение катка происходит без скольжения, сопротивление качению отсутствует. Центр масс блока расположен на оси его вращения. К грузу приложена возмущающая сила
. Качение катка происходит без скольжения, сопротивление качению отсутствует. Центр масс блока расположен на оси его вращения. К грузу приложена возмущающая сила  . При движении системы нити всегда натянуты. Схема механической системы представлена ниже:
. При движении системы нити всегда натянуты. Схема механической системы представлена ниже:
Исследовать движение механической системы. Определить реакции внешних и внутренних связей, если
 – массы груза, блока и катка,
– массы груза, блока и катка,
c – коэффициент жесткости пружины,
 – коэффициент демпфирования,
– коэффициент демпфирования,
 - радиусы ступеней невесомого блока 2,
- радиусы ступеней невесомого блока 2,
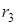 – радиус блока 3,
– радиус блока 3,
 – радиусы ступеней катка 4 и радиус инерции относительно оси, проходящей через центр масс,
– радиусы ступеней катка 4 и радиус инерции относительно оси, проходящей через центр масс,
 – предельное значение коэффициента сцепления катка 4 и опорной плоскости,
– предельное значение коэффициента сцепления катка 4 и опорной плоскости,
 – предельное значение удлинения пружины;
– предельное значение удлинения пружины;
 — начальная координата и начальная скорость груза.
— начальная координата и начальная скорость груза.
Исходные данные:

|

|

|

|

|

|

|

|

|

|

|

|
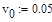
|
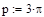
|
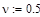
|

|

|

|
Составление дифференциального уравнения движения механической системы
Рассматриваемая механическая система имеет одну степень свободы: это обеспечивается условиями, принятыми при формулировке задания, — тела являются абсолютно твердыми, нити — нерастяжимыми и всегда натянутыми, проскальзывание при движении катка отсутствует. Следовательно, для задания положения системы нужен один параметр. Будем определять положение системы с помощью координаты S, задающей положение центра масс груза (рис.2). Начало отсчета координаты Sсовместим с положением центра масс груза при равновесии системы. Углы поворота блока  и катка
и катка  отсчитываем по ходу часовой стрелки. Положение центра масс катка
отсчитываем по ходу часовой стрелки. Положение центра масс катка  определяем координатой
определяем координатой
 , отсчитываемой от положения центра масс катка при равновесии системы:
, отсчитываемой от положения центра масс катка при равновесии системы:
если  , то
, то  ,
,  ,
,  и
и 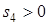 и наоборот, причем нулевому значению координаты Sсоответствуют нулевые значения координат
и наоборот, причем нулевому значению координаты Sсоответствуют нулевые значения координат  ,
,  ,
,  и
и  .
.
Для составления дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в дифференциальной форме:
 (1)
(1)
где: T— кинетическая энергия системы,  — сумма мощностей внешних
— сумма мощностей внешних
сил,  — сумма мощностей внутренних сил.
— сумма мощностей внутренних сил.
Пусть в произвольный момент система занимает положение, в котором
S>0, а скорость груза  направлена вдоль опорной плоскости в положительном направлении координаты S.
направлена вдоль опорной плоскости в положительном направлении координаты S.
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему.
Груз 1 совершает поступательное движение. Его кинетическая энергия:
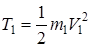
Блок 2 невесом и его кинетическая энергия равна 0.
Блок 3 совершает вращательное движение вокруг неподвижной оси. Его кинетическая энергия:

где  — момент инерции блока 3 относительно оси вращения,
— момент инерции блока 3 относительно оси вращения,  —
—
модуль угловой скорости.
Каток 4 совершает плоскопараллельное движение, поэтому его кинетическая энергия равна:

Тогда кинетическая энергия всего механизма имеет вид:
 (2)
(2)
Так как механическая система (мс) имеет 1 степень свободы, то величины  легко выражаются через
легко выражаются через  . Связи между этими величинами будут иметь вид:
. Связи между этими величинами будут иметь вид:
 (3)
(3)
Блок 3 – сплошной однородный цилиндр, для катка 4 известен радиус инерции, поэтому моменты инерции этих тел относительно осей, проходящих через их центры масс и перпендикулярных плоскости чертежа, будут вычисляться:


Подставляя моменты инерции и выражения (3) в формулу (2), получим полную кинетическую энергию системы:
 (4)
(4)
где величина  называется приведенной массой.
называется приведенной массой. 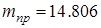 кг
кг
Теперь вычислим правую часть уравнения (1) – сумму мощностей внешних и внутренних сил, при этом учтем, что мощность силы равна скалярному произведению вектора силы на скорость точки приложения силы, а мощность пары сил – скалярному произведению вектора пары на угловую скорость твердого тела, к которому приложена пара:

Или
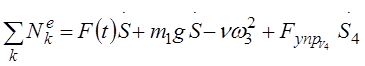
Рассматриваемая нами механическая система является неизменяемой, так как входящие в систему тела абсолютно твердые, а нити — абсолютно гибкие и нерастяжимые. Следовательно, скорости их точек относительно друг друга равны нулю и сумма мощностей внутренних сил также будет равна нулю
 (6)
(6)
С учетом кинематических соотношений (3) сумму мощностей внешних
сил преобразуем к виду:
 (7)
(7)
Где
 - приведенная сила.
- приведенная сила.
Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины  равно сумме статического
равно сумме статического  и динамического
и динамического  удлинений
удлинений 
Тогда

Приведенная сила в развернутом виде примет вид:
 (8)
(8)
Где  - приведенная жесткость,
- приведенная жесткость,
 - приведенный коэффициент сопротивления.
- приведенный коэффициент сопротивления.
Подставляя выражения (4), (6) и (7) в (1), получаем после сокращения на  дифференциальное уравнение движения системы:
дифференциальное уравнение движения системы:
 (9)
(9)
Учтем, что при равновесии системы (возмущающая сила отсутствует) скорость и ускорение груза равны нулю по определению 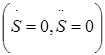 , а координата груза равна нулю в силу постановки задачи (начало отсчета совпадает с положением равновесия груза 1 S=0). В этом случае уравнение (9) приводится к виду
, а координата груза равна нулю в силу постановки задачи (начало отсчета совпадает с положением равновесия груза 1 S=0). В этом случае уравнение (9) приводится к виду  , и условием равновесия системы будет служить уравнение
, и условием равновесия системы будет служить уравнение

Откуда
 (10)
(10)
Подставляя (10) в уравнение (9) и учитывая формулу (8) для приведенной силы, получаем дифференциальное уравнение движения системы

Представим данное уравнение в виде:
 (11)
(11)
где введены коэффициенты, имеющие определенный физический смысл:
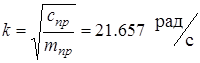 - частота собственных колебаний,
- частота собственных колебаний,
 - показатель степени затухания колебаний.
- показатель степени затухания колебаний.
 - относительная амплитуда возмущающей силы.
- относительная амплитуда возмущающей силы.
Начальные условия:
 (12)
(12)
Уравнения (11), (12) представляют математическую модель для решения второй задачи динамики.