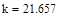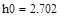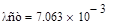Найдем решение дифференциального уравнения движения механической системы (11). Данное дифференциальное уравнение относится к классу линейных неоднородных дифференциальных уравнений с постоянными коэффициентами. Решение таких уравнений можно найти аналитически. Общее решение неоднородного дифференциального уравнения (11) складывается из общего решения однородного уравнения 
(16)
соответствующего данному неоднородному уравнению, и какого-либо частного решения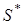 
уравнения (11), т.е.
(17)
Решение однородного уравнения (16) ищем в виде функции
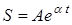(18)
Подставив (18) в (16), получим:
Так как мы ищем нетривиальное решение, то 
. Следовательно, должно выполняться условие
Данное уравнение называется характеристическим уравнением дифференциального уравнения (16). Это уравнение имеет два корня:
Вид общего решения уравнения (16) зависит от типа корней его характеристического уравнения. Возможны следующие случаи:
1) n<k – корни характеристического уравнения комплексные сопряженные:
и общее решение однородного уравнения имеет вид
(19)
Здесь 
- постоянные интегрирования.
2) n>k – корни характеристического уравнения действительные и различные
и общее решение однородного уравнения имеет вид
3) n=k - корни характеристического уравнения кратные: 
и общее решение однородного уравнения имеет вид
В рассматриваемом случае 
, 
. Поскольку n<k, то общее решение однородного уравнения (16) имеет вид:
или 
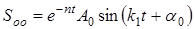(20)
Здесь 
, а коэффициенты 
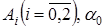связаны между собой соотношениями:
Определим частное решение неоднородного дифференциального уравнения (11). Данное решение ищем в виде правой части
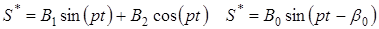(21)
где коэффициенты 
связаны между собой соотношениями
Подставляя (21) в уравнение (11), после несложных преобразований получим
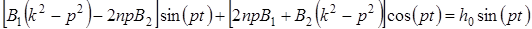
Приравнивая коэффициенты при функциях sin(pt) и cos(pt) в правой и левой частях последнего равенства, получаем систему алгебраических уравнений для определения постоянных 
:
Решая данную систему, найдем выражения для коэффициентов:
Таким образом, решение (21) найдено. Складывая (20) и (21), получаем общее решение неоднородного уравнения (11):
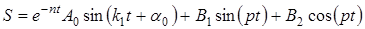(22)
Константы 
и 
определяются из начальных условий (12). Для этого найдем производную по времени от перемещения груза
(23)
Подчинив (22) и (23) начальным условиям, получим систему уравнений
относительно искомых констант
Решая систему, получим:
(24)
Таким образом, закон движения имеет вид:
Из последней формулы следует, что движение системы представляет собой наложение двух движений:
1) собственного движения (первое слагаемое справа), которое представляет собой затухающие колебания частоты 
, так как множитель 
при 
;
2) вынужденных колебаний постоянной амплитуды 
(второе слагаемое справа), происходящих с частотой возмущающей силы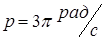 
, причем фаза вынужденных колебаний отстает от фазы возмущающей силы на величину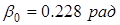 
Поскольку по истечении некоторого промежутка времени собственное движение затухает, то определяющим движением системы являются вынужденные колебания.
Результаты расчетов
Ниже приведен пример документа Mathcad, в котором реализована процедура вычисления закона движения груза, его скорости и ускорения, а также динамических реакций внешних и внутренних связей.
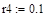
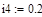
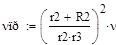
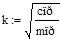
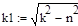
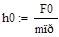
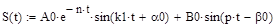
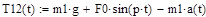
Результаты расчетов:
