Стохастическая связь - это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величин x1,x2,...,xn (случайных или неслучайных) изменением закона распределения. Это обусловливается тем, что зависимая переменная (результативный признак), кроме рассматриваемых независимых, подвержена влиянию ряда неучтенных или неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибок измерения переменных. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.
Характерной особенностью стохастических связей является то, что они проявляются во всей совокупности, а не в каждой ее единице (причем не известен ни полный перечень факторов, определяющих значение результативного признака, ни точный механизм их функционирования и взаимодействия с результативным признаком). Всегда имеет место влияние случайного. Появляющиеся различные значения зависимой переменной - реализации случайной величины.
Модель стохастической связи может быть представлена в общем виде уравнением:
ŷi = f(xi) + εi
где ŷi - расчетное значение результативного признака;
f(xi) - часть результативного признака, сформировавшаяся под воз- действием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком;
εi - часть результативного признака, возникшая вследствие действия неконтролируемых или неучтенных факторов, а также измерения признаков неизбежно сопровождающегося некоторыми случайными ошибками.
Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо.
В социально-экономической жизни приходится сталкиваться со многими явлениями, имеющими вероятностный характер. Например, уровень производительности труда рабочих стохастически связан с целым комплексом факторов: квалификацией, стажем работы, уровнем механизации и автоматизации производства, интенсивностью труда, простоями, состоянием здоровья работника, его настроением, атмосферным давлением и др. Полный перечень факторов неизвестен. Кроме того, неодинаково действие любого известного фактора на уровень производительности труда каждого рабочего. Изменение атмосферного давления, к примеру, значительно снижает работоспособность рабочих, страдающих заболеваниями сердечно-сосудистой системы, и практически не сказывается на производительности труда здоровых. В результате - при одинаковых возможностях наблюдается распределение значений дневной выработки рабочих. Такое распределение носит условный характер, поскольку оно связано с фиксированными значениями факторных признаков. Различия условных распределений имеют выраженную направленность связи (например, выработка растет с повышением квалификации рабочего). Эту направленность связи можно раскрыть более наглядно, если ограничиться рассмотрением только одного аспекта стохастической связи - изучением вместо условных распределений лишь одного их параметра - условного математического ожидания (частные случаи стохастической связи - корреляционная и регрессионная).
Корреляционная связь существует там, где взаимосвязанные явления характеризуются только случайными величинами. При такой связи среднее значение (математическое ожидание) случайной величины результативного признака у закономерно изменяется в зависимости от изменения другой величины х или других случайных величин x1,x2,...,xn. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом. Только при достаточно большом количестве случаев каждому значению случайного признака х будет соответствовать распределение средних значений случайного признака у. Наличие корреляционных связей присуще многим общественным явлениям.
Известно, что увеличение количества внесенных удобрений ведет к повышению урожайности. Это справедливое положение, подтверждаемое в массе явлений, совсем не означает, что на отдельных одинаково удобренных участках будет одинаковая урожайность одной и той же сельскохозяйственной культуры. Вероятнее всего, уровни урожайности будут различаться. Кроме того, существует вероятность, что более высокая урожайность может наблюдаться на менее удобренных участках: на урожайность влияет не только количество внесенных в почву удобрений, но и другие, неучтенные факторы (качество семян, предшествующие культуры, рельеф местности, агротехника земледелия, сроки и качество посева и уборки). Но если в анализ включить достаточно большое число площадей, то обнаружится прямая корреляционная зависимость между количеством внесенных удобрений (в допустимых пределах) и средним уровнем урожайности. Значит, важная особенность корреляционных связей (как и других стохастических) состоит в том, что они обнаруживаются не в единичных случаях, а в массовых явлениях и требуют для своего исследования массовых наблюдений, т. е. статистических данных.
Корреляционная связь - понятие более узкое, чем стохастическая связь. Последняя может отражаться не только в изменении средней величины, но и в вариации одного признака в зависимости от другого, т. е. любой другой характеристики вариации. Таким образом, корреляционная связь, является частным случаем стохастической связи.
Прямые и обратные связи. В зависимости от направления действия функциональные и стохастические связи могут быть прямыми и обратными. При прямой связи направление изменения результативного признака совпадает с направлением изменения признака-фактора, т. е. с увеличением факторного признака увеличивается и результативный, и наоборот, с уменьшением факторного признака уменьшается и результативный признак. В противном случае между рассматриваемыми величинами существуют обратные связи. Например, чем выше квалификация рабочего (разряд), тем выше уровень производительности труда - прямая связь. А чем выше производительность труда, тем ниже себестоимость единицы продукции - обратная связь.
Прямолинейные и криволинейные связи. По аналитическому выражению (форме) связи могут быть прямолинейными и криволинейными. При прямолинейной связи с возрастанием значения факторного признака происходит непрерывное возрастание (или убывание) значений результативного признака. Математически такая связь представляется уравнением прямой, а графически - прямой линией. Отсюда ее более короткое название - линейная связь.
При криволинейных связях с возрастанием значения факторного признака возрастание (или убывание) результативного признака происходит неравномерно или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, параболой и т.д.).
Однофакторные и многофакторные связи. По количеству факторов, действующих на результативный признак, связи различаются однофакторные (один фактор) и многофакторные (два и более факторов). Однофакторные (простые) связи обычно называются парными (так как рассматривается пара признаков). Например, корреляционная связь между прибылью и производительностью труда. В случае многофакторной (множественной) связи имеют в виду, что все факторы действуют комплексно, т.е. одновременно и во взаимосвязи, например, корреляционная связь между производительностью труда и уровнем организации труда, автоматизации производства, квалификации рабочих, производственным стажем, простоями и другими факторными признаками.
С помошью множественной корреляции можно охватить весь комплекс факторных признаков и объективно отразить существующие множественные связи.
9.2.2. Статистическое моделирование связи методом корреляционного и регрессионного анализа
В общем виде задача статистики в области изучения взаимосвязей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на
результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.
Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых, должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа - выбор типа модели (формы связи), установление степени влияния независимых переменных1 на зависимую и определение расчетных значений зависимой переменной (функции регрессии).
Решение всех названных задач приводит к необходимости комплексного использования этих методов.
9.2.2.2. Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный линейный корреляционный и регрессионный анализ)
Наиболее разработанной в теории статистики является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака х на результативный признак у и представляющая собой однофакторный корреляционный и регрессионный анализ. Овладение теорией и практикой построения и анализа двухмерной модели корреляционного и регрессионного анализа представляет собой исходную основу для изучения многофакторных стохастических связей.
Важнейшим этапом построения регрессионной модели (уравнения регрессии) является установление в анализе исходной информации математической функции. Сложность заключается в том, что из множества функций необходимо найти такую, которая лучше других выражает реально существующие связи между анализируемыми признаками. Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически - перебором и оценкой функций разных типов и т.п.
При изучении связи экономических показателей производства (деятельности) используют различного вида уравнения прямолинейной и криволинейной связи. Внимание к линейным связям объясняется ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные формы связи для выполнения расчетов преобразуют (путем логарифмирования или замены переменных) в линейную форму. Уравнение однофакторной (парной) линейной корреляционной связи имеет вид:
ŷ = a0 + a1x
где ŷ - теоретические значения результативного признака, полученные по уравнению регрессии;
a0, a1 - коэффициенты (параметры) уравнения регрессии.
Поскольку a0 является средним значением у в точке x = 0 экономическая интерпретация часто затруднена или вообще невозможна.
Коэффициент парной линейной регрессии a1 имеет смысл показателя силы связи между вариацией факторного признака х и вариацией результативного признака у. Уравнение (9.2)
показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т. е. вариацию у, приходящуюся на единицу вариации х. Знак #ALARM-FONT# указывает направление этого изменения.
Параметры уравнения a0, a1 находят методом наименьших квадратов (метод решения систем уравнений, при котором в качестве решения принимается точка минимума суммы квадратов отклонений), т. е. в основу этого метода положено требование минимальности сумм квадратов отклонений эмпирических данных yi от выровненных ŷ:

Для нахождения минимума данной функции приравняем к нулю ее частные производные и получим систему двух линейных уравнений, которая называется системой нормальных уравнений:
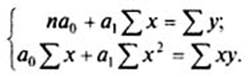
Решим эту систему в общем виде:

Параметры уравнения парной линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же результат:

Определив значения a0, a1 и подставив их в уравнение связи ŷ = a0 + a1 находим значения ŷ, зависящие только от заданного значения х.
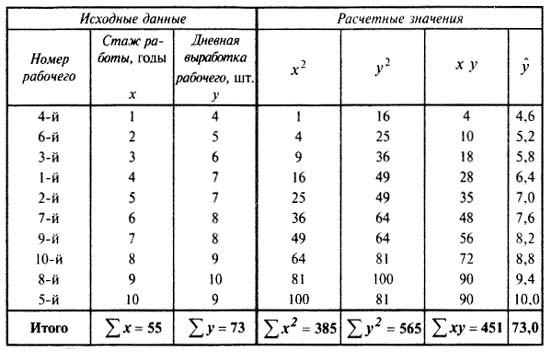
Пример 1. Рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда у от стажа работы х по данным табл. 9.1 (10 рабочих одной бригады заняты производством радиоэлектронных изделий, данные ранжированы по стажу их работы).
Исходя из экономических соображений стаж работы выбран в качестве независимой переменной х. Сопоставление данных параллельных рядов признаков х и у (табл. 9.1) показывает, что с возрастанием признака х (стажа работы), растет, хотя и не всегда, результативный признак у (производительность труда). Следовательно, между х и у существует прямая зависимость, пусть неполная, но выраженная достаточно ясно.
Для уточнения формы связи между рассматриваемыми признаками используем графический метод. Нанесем на график точки, соответствующие значениям х, y, получим корреляционное поле, а соединив их отрезками, - ломаную регрессии1 (рис. 9.1).
Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 9.1), которая может быть выражена простым линейным уравнением регрессии:
ŷ = a0 + a1
где ŷ - теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии;
a0, a1 - неизвестные параметры уравнения регрессии;
x - стаж работы рабочих, годы.

Пользуясь расчетными значениями (см. табл. 9.1), исчислим параметры для данного уравнения регрессии:

Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного простого уравнения регрессии:
ŷ = 4,0 + 0,6
Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значения у, найденные по данному уравнению, приведены в табл. 9.1. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм ∑y = ∑ŷ (при этом возможно некоторое расхождение вследствие округления расчетов).
1 Данный метод эффективен лишь при небольшом объеме совокупности и достаточно тесной связи между признаками. Более наглядную характеристику связи можно получить, построив ломаную регрессии по частным средним.
9.2.2.3 Проверка адекватности регрессионной модели
Для практического использования моделей регрессии очень важна их адекватность, т. е. соответствие фактическим статистическим данным.
Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции - параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей.
При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин.
Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n < 30) осуществляют с помощью t-критерия Стьюдента. При этом вычисляют расчетные (фактические) значения t -критерия:
для параметра a0
 (9.4)
(9.4)
для параметра a1
 (9.5)
(9.5)

где n - объем выборки;
 среднее квадратическое отклонение результативного признака у от выравненных значений ŷ;
среднее квадратическое отклонение результативного признака у от выравненных значений ŷ;
 или
или  среднее квадратическое отклонение факторного признака х от общей средней x-.
среднее квадратическое отклонение факторного признака х от общей средней x-.
Вычисленные по формулам (9.4) и (9.5) значения, сравнивают с критическими t, которые определяют по таблице Стьюдента с учетом принятого уровня значимости1 а и числом
степеней свободы2 вариации v = n - 2. В социально-экономических исследованиях уровень значимости a обычно принимают равным 0,05. Параметр признается значимым (существенным) при условии, если tрасч > tтабл. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями. Для проверки значимости коэффициентов регрессии исследуемого уравнения ŷ = 4,0 + 0,6x исчислим t -критерий Стьюдента с v = 10-2 = 8 степенями свободы. Рассмотрим вспомогательную таблицу (табл. 9.2).
Таблица 9.2
Расчетные значения, необходимые для исчисления 
Средние квадратические отклонения (см. табл. 9.1):


Расчетные значения г-критерия Стьюдента:

По таблице распределения Стьюдента для v = 8 находим критическое значение t -критерия: (tтабл = 3,307 при a = 0,05).
Поскольку расчетное значение tрасч > tтабл, оба параметра a0, a1 признаются значимыми (отклоняется гипотеза о том, что каждый из этих параметров в действительности равен нулю, и лишь в силу случайных обстоятельств оказался равным проверяемой величине).
Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у. Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционньм отношением ηэ когда δ2 (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней:  .
.
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения - теоретическое.
Теоретическое корреляционное отношение η представляет собой относительную величину, получающуюся в результате сравнения среднего квадратического отклонения выровненных значений результативного признака δ, т. е. рассчитанных по уравнению регрессии, со средним квадратическим отклонением эмпирических (фактических) значений результативного признака σ:
 (9.6)
(9.6)
Изменение значения η объясняется влиянием факторного признака.
В основе расчета корреляционного отношения лежит правило сложения дисперсий (см. главу 5), т. е.  - отражает вариацию у за счет всех остальных факторов, кроме х, т. е. является остаточной дисперсией:
- отражает вариацию у за счет всех остальных факторов, кроме х, т. е. является остаточной дисперсией:

Тогда формула теоретического корреляционного отношения примет вид:

Подкоренное выражение корреляционного отношения представляет собой коэффициент детерминации (меры определенности, причинности). Коэффициент детерминации показывает долю вариации результативного признака под влиянием вариации признака-фактора.
Теоретическое корреляционное отношение применяется для измерения тесноты связи при линейной и криволинейной зависимостях между результативным и факторным признаком. При криволинейных связях теоретическое корреляционное отношение, исчисляемое по формулам (9.7), (9.8), часто называют индексом корреляции R. При значительной корреляции расчет по формулам (9.7) и (9.8) значительно проще, так как отклонение (ŷ - y), как правило, по значению меньше, чем отклонение (ŷ - y-).
Как видно из формул (9.7) и (9.8), корреляционное отношение может находиться в пределах от 0 до 1, т. е. (0 ≤ η ≤ 1) Чем ближе корреляционное отношение к 1, тем связь между признаками теснее.
Проиллюстрируем расчет теоретического корреляционного отношения как меры тесноты связи на примере, рассмотренном в табл.9.1, для которого по уравнению прямой регрессии ŷ = 4 + 0,6х найдены значения дневной выработки каждого рабочего.
Теоретическое корреляционное отношение рассчитываем двумя способами (см. данные табл.9.2):
по формуле (9.6) 
по формуле (9.8) 
Полученное значение теоретического корреляционного отношения свидетельствует о возможном наличии весьма тесной прямой зависимости между рассматриваемыми признаками.
Коэффициент детерминации равен 0,925. Отсюда заключаем, что 92,5% общей вариации выработки в изучаемой бригаде обусловлено вариацией фактора - стажа работы рабочих (и только 7,5% обшей вариации нельзя объяснить изменением стажа работы).
Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - линейный коэффициент корреляции 1.

где n - число наблюдений.
Для практических вычислений при малом числе наблюдений. п ≤ (20 - 30), линейный коэффициент корреляции удобнее исчислять по следующей формуле:

Значение линейного коэффициента корреляции важно для исследования социально-экономических явлений и процессов, распределение которых близко к нормальному. Он принимает значения в интервале: -1 ≤ r ≤ +1.
Отрицательные значения указывают на обратную связь, положительные - на прямую. При r = 0 линейная связь
отсутствует. Чем ближе коэффициент корреляции по абсолютной величине к единице, тем теснее связь между признаками. И. наконец, при r = ± 1 связь - функциональная.
Используем данные табл. 9.1 и рассчитаем линейный коэффициент корреляции по формуле (9.10):

Квадрат линейного коэффициента корреляции r2 называется линейным коэффициентом детерминации. Из определения коэффициента детерминации очевидно, что его числовое значение всегда заключено в пределах от 0 до 1, т. е. 0 ≤ r2 ≤ 1. Степень тесноты связи полностью соответствует теоретическому корреляционному отношению, которое является более универсальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.
Факт совпадений и несовпадений значений теоретического корреляционного отношения η и линейного коэффициента корреляции r используется для оценки формы связи.
Выше отмечайтесь, что посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции - только прямолинейной. Следовательно, значения η и r совпадают только при наличии прямолинейной связи. Несовпадение этих значений свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов η2 и r 2 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной. В приведенном ранее примере совпадение значений n и r (η = r = 0,962) дает основание считать связь между выработкой рабочих и их стажем прямолинейной.
Показатели тесноты связи, исчисленные по данным сравнительно небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.
Для оценки значимости коэффициента корреляции r используют t -критерий Стьюдента, который применяется при t -распределении, отличном от нормального.
При линейной однофакторной связи t -критерий можно рассчитать по формуле:
 (9.11)
(9.11)
где (n -2) - число степеней свободы при заданном уровне значимости a и объеме выборки n.
Полученное значение tрасч сравнивают с табличным значением t -критерия (для а = 0.05 и 0.01). Если рассчитанное значение tрасч превосходит табличное значение критерия tтабл, то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т. е. отклоняется гипотеза о его случайности).
Так. для коэффициента корреляции между выработкой и стажем работы получим:

Это значительно больше критического значения t для п - 2 = 8 степеней свободы и a == 0,01 (tтабл = 3,356), что свидетельствует о значимости коэффициента корреляции и существенности связи между выработкой и стажем работы.
Таким образом, построенная регрессионная модель ŷ = 4+0,6 х в целом адекватна, и выводы, полученные по результатам малой выборки, можно с достаточной вероятностью распространить на всю гипотетическую генеральную совокупность.
1 Уровень значимости применительно к проверке статистических гипотез - это вероятность, с которой может быть опровергнута гипотеза о том или ином законе распределения. Так, двум доверительным вероятностям 0.95 и 0.99 соответствует 5%-ный и 1%-ный уровни значимости, т.е.
2 Число степеней свободы вариации представляет собой число свободно (неограниченно) варьирующих элементов совокупности где - число факторных признаков в уравнении
1 Коэффициент корреляции был предложен английским математиком К.Пирсоном.
9.2.2.4. Экономическая интерпретация параметров регрессии
После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель).
В рассмотренном уравнении ŷ=4+0,6 х, характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр a 1 > 0. Следовательно, с возрастанием стажа выработка, как и ожидалось, также увеличивается.
Из уравнения следует, что возрастание на 1 год стажа рабочего приводит к увеличению им дневной выработки в среднем на 0,6 изделия (величину параметра a 1).
Для удобства интерпретации параметра a 1 используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %:
 (9.12)
(9.12)