Рассмотрим частные случаи нахождения точки МЦС.
1. Если плоское движение осуществляется путем качения цилиндрического тела по поверхности другого тела без скольжения, причем второе тело неподвижно, то точка касания Р имеет в данный момент времени скорость, равную нулю, следовательно, является МЦС (рис. 6.13, а), тело мгновенно вращается относительно точки касания Р.
Иначе говоря, Если на перпендикуляре к вектору скорости есть точка, скорость в которой равна нулю, то эта точка будет точкой МЦС.
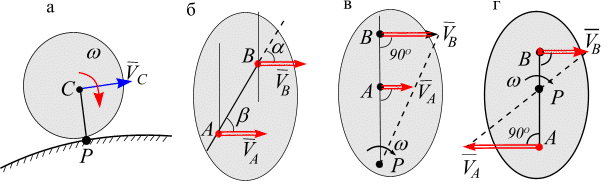
Рис. 6.13
2. Если в двух точках А и В твердого тела 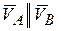 , при этом прямая АВ, соединяющая эти точки, не перпендикулярна векторам
, при этом прямая АВ, соединяющая эти точки, не перпендикулярна векторам 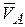 и
и 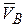
(рис. 6.13, б), то перпендикуляры к 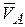 и к
и к 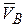 пересекутся в в бесконечности, т.е. точка МЦС
пересекутся в в бесконечности, т.е. точка МЦС 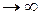 , тогда
, тогда 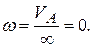 Из общей теоремы кинематики имеем, что
Из общей теоремы кинематики имеем, что 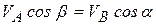 (
(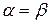 ), тогда
), тогда 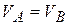 . Следовательно, скорости всех точек тела в данный момент равны между собой по модулю и по направлению, твердое тело движется мгновенно поступательно. Примгновенно поступательном движении угловая скорость тела равна нулю, угловое ускорение не всегда равно нулю.
. Следовательно, скорости всех точек тела в данный момент равны между собой по модулю и по направлению, твердое тело движется мгновенно поступательно. Примгновенно поступательном движении угловая скорость тела равна нулю, угловое ускорение не всегда равно нулю.
3. Если в двух точках А и В твердого тела 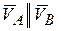 , при этом прямая АВ, соединяющая эти точки, перпендикулярна векторам
, при этом прямая АВ, соединяющая эти точки, перпендикулярна векторам 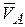 и
и 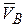 и
и 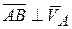 ,
, 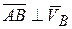 (рис. 6.13, в, г) то положение точки МЦС определяется построениями, показанными на рис. 6.13 в, г, тело имеет мгновенно-вращательное движение вокруг точки МЦС ( точка Р). При этом модули скоростей точек тела связаны соотношением
(рис. 6.13, в, г) то положение точки МЦС определяется построениями, показанными на рис. 6.13 в, г, тело имеет мгновенно-вращательное движение вокруг точки МЦС ( точка Р). При этом модули скоростей точек тела связаны соотношением
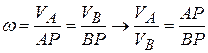 .
.
Механизмы
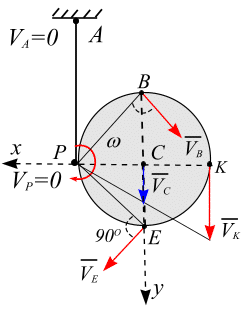 Рис. 6.14 Рис. 6.14
| Маятник Максвелла.Маятник Максвелла состоит из диска радиусом 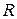 , на который намотана нерастяжимая нить, конец которой закреплен в точке А (рис. 6.14). Вычислим скорости на ободе диска, если известна скорость его центра , на который намотана нерастяжимая нить, конец которой закреплен в точке А (рис. 6.14). Вычислим скорости на ободе диска, если известна скорость его центра 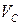 .
Свяжем декартову систему координат .
Свяжем декартову систему координат 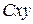 с центром диска. Скорость центра диска с центром диска. Скорость центра диска 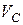 параллельна оси параллельна оси 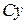 . Ось . Ось 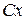 проходит через точку проходит через точку 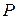 . Нить . Нить 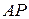 неподвижна, следовательно неподвижна, следовательно 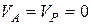 . .
|
Следовательно, точка Р является точкой МЦС. Модули скоростей точек диска связаны соотношением
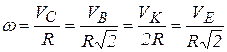 .
.
Кривошипно – шатунный механизм. Кривошипно – шатунный механизм состоит из кривошипа ОА, шатуна АВ и ползуна В (рис. 6.15).
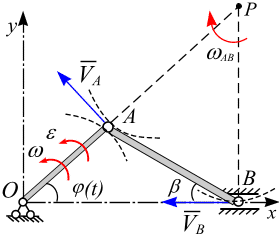 Рис. 6.15 Рис. 6.15
| Кривошип ОА длиной 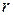 вращается в плоскости относительно неподвижной точки вращается в плоскости относительно неподвижной точки 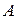 с угловой скоростью с угловой скоростью 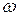 и угловым ускорением и угловым ускорением  .
Совместим декартову систему координат с точкой О. Вычислим скорость ползуна .
Совместим декартову систему координат с точкой О. Вычислим скорость ползуна  .
Имеем: .
Имеем:
|
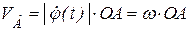 (м/с).
(м/с).
Вектор скорости 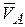 направлен перпендикулярно ОА в сторону вращения кривошипа (рис. 6.15). Ползун В движется поступательно вдоль дорожек, следовательно скорость ползуна
направлен перпендикулярно ОА в сторону вращения кривошипа (рис. 6.15). Ползун В движется поступательно вдоль дорожек, следовательно скорость ползуна 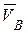 направлена по оси
направлена по оси 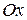 . Скорости в точках А и В шатуна АВ не параллельны, следовательно шатун совершает плоскопараллельное движение. Восстановим перпендикуляры к векторам
. Скорости в точках А и В шатуна АВ не параллельны, следовательно шатун совершает плоскопараллельное движение. Восстановим перпендикуляры к векторам 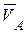 и
и 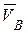 . Точка МЦС (точка Р) лежит на их пересечении
. Точка МЦС (точка Р) лежит на их пересечении
(рис. 6.15). Все точки шатуна мгновенно движутся по окружностям соответствующих радиусов с центром вращения в точке МЦС (точка А – по радиусу 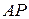 , точка В – по радиусу
, точка В – по радиусу 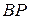 , при этом угловая скорость вращения шатуна и модули скоростей точек шатуна связаны соотношением:
, при этом угловая скорость вращения шатуна и модули скоростей точек шатуна связаны соотношением:
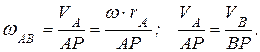
Скорость ползуна (скорость в точке В):
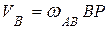 .
.
Рассмотрим частные случаи.
1. Движение шатуна в момент времени, когда угол 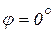
(рис. 6.16, а).
Вектор скорости кривошипа в точке А ( 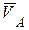 ) направлен по оси
) направлен по оси 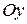 . Восстановим перпендикуляры к векторам
. Восстановим перпендикуляры к векторам 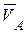 и
и 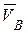 . Точка МЦС (точка Р) лежит на их пересечении и совпадает с точкой В. Следовательно, точка В является в этом положении механизма точкой МЦС, тогда
. Точка МЦС (точка Р) лежит на их пересечении и совпадает с точкой В. Следовательно, точка В является в этом положении механизма точкой МЦС, тогда 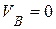 . В этом положении шатун АВ совершает мгновенное вращение вокруг мгновенно неподвижной точки В с угловой скоростью
. В этом положении шатун АВ совершает мгновенное вращение вокруг мгновенно неподвижной точки В с угловой скоростью 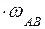 :
:
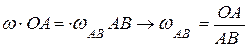 .
.
Распределение скоростей точек шатуна показано на рис. 6.16, а.
2. Движение шатуна в момент времени, когда угол 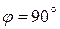
(рис. 6.16, б).
| а | 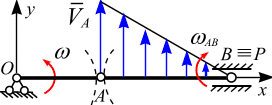
| б | 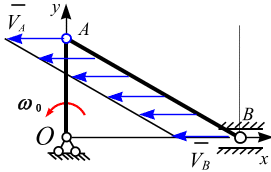
|
| Рис. 6.16 |
Вектор скорости кривошипа в точке А ( 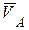 ) направлен по оси
) направлен по оси 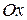 . Скорости
. Скорости 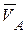 и
и 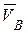 направлены параллельно друг другу, перпендикуляры к
направлены параллельно друг другу, перпендикуляры к 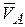 и
и 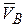 пересекутся в бесконечности, т.е. точка МЦС
пересекутся в бесконечности, т.е. точка МЦС 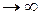 , тогда
, тогда 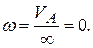 Следовательно, в этом положении шатун совершает мгновенно-поступательное движение, и все точки шатуна АВ имеют одинаковую скорость, равную
Следовательно, в этом положении шатун совершает мгновенно-поступательное движение, и все точки шатуна АВ имеют одинаковую скорость, равную 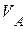 .
.
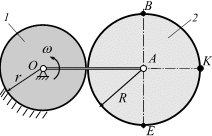 Рис. 6.17 Рис. 6.17
| Планетарный механизм.Планетарный механизм состоит из неподвижного диска 1 радиусом 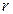 , кривошипа ОА и подвижного диска, радиусом , кривошипа ОА и подвижного диска, радиусом 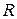 , закрепленного а точке , закрепленного а точке 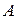 кривошипа кривошипа 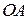 (рис.6.17). (рис.6.17).
|
Кривошип ОА вращается с угловой скоростью 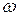 и приводит в движение подвижный диск 2. Вычислим скорость в точках
и приводит в движение подвижный диск 2. Вычислим скорость в точках 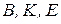 , лежащие на ободе подвижного диска.
, лежащие на ободе подвижного диска.
Имеем (рис. 6.18):
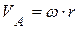 .
.
Свяжем декартову систему координат 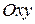 с центром неподвижного диска. Скорость в точке А кривошипа параллельна оси
с центром неподвижного диска. Скорость в точке А кривошипа параллельна оси  . Точка соприкосновения неподвижного и подвижного дисков будет точкой МЦС
. Точка соприкосновения неподвижного и подвижного дисков будет точкой МЦС  точка Р (рис. 6.18).
точка Р (рис. 6.18).
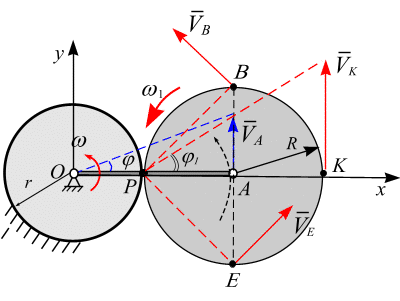
Рис. 6.18
Запишем уравнения связи. Точка А имеет два радиуса вращения – 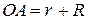 и
и 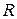 , поэтому
, поэтому
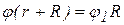
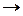
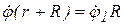
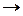
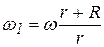 .
.
При этом модули скоростей точек, лежащих на ободе подвижного диска связаны соотношением
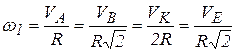 .
.
Подвижный диск движется плоскопараллельно.
§ 6.6. Ускорение при плоском движении твердого тела [1]
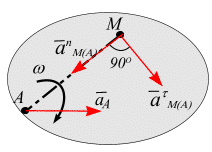 Рис. 6.19
Рис. 6.19
|
Ускорение какой-либо точки тела при его плоскопараллельном движении равно векторной сумме ускорения полюса 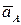 и ускорения этой точки при вращательном движении тела вокруг полюса (рис. 6.19):
и ускорения этой точки при вращательном движении тела вокруг полюса (рис. 6.19):
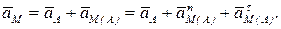 (6.5)
(6.5)
Здесь:
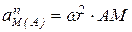 – нормальное ускорение точки М во вращении вокруг полюса
– нормальное ускорение точки М во вращении вокруг полюса 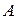 ;
;
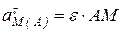 – касательное ускорение точки М во вращении вокруг полюса А.
– касательное ускорение точки М во вращении вокруг полюса А.
Рис. 6.20 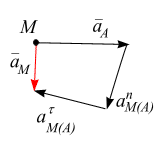
| Модуль и направление ускорения точки М – 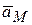 , можно найти геометрически построением в выбранном масштабе многоугольника из векторов ускорений , можно найти геометрически построением в выбранном масштабе многоугольника из векторов ускорений 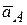 , , 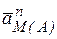 , , 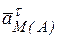 , , 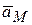 для точки М (рис. 6.20). для точки М (рис. 6.20).
|
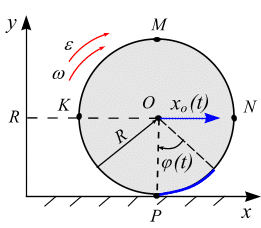 Пример 6.2. Колесо радиусом R катится без скольжения по линейному рельсу. Центр
Пример 6.2. Колесо радиусом R катится без скольжения по линейному рельсу. Центр 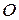 колеса движется согласно уравнению
колеса движется согласно уравнению 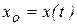 . Вычислить в момент времени
. Вычислить в момент времени 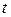 ускорения точек Р, М, К, N расположенных на ободе колеса, как показано на рис. 6.21.
ускорения точек Р, М, К, N расположенных на ободе колеса, как показано на рис. 6.21.
Решение. За полюс выберем точку 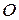 .Уравнения вращения колеса вокруг полюса имеет вид
.Уравнения вращения колеса вокруг полюса имеет вид
Рис. 6.21 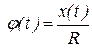 .
.
Вычислим угловую скорость 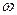 , угловое ускорение
, угловое ускорение 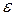 и ускорение полюса. Имеем
и ускорение полюса. Имеем
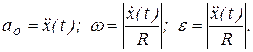
Направление 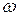 и
и 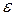 показано дуговыми стрелками (рис. 6. 22).
показано дуговыми стрелками (рис. 6. 22).
Ускорение точки М вычислим по формуле
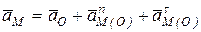 .
.
Приводим к точке М ускорение полюса 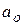 , рис. 6.22, а. Для нормального и касательного ускорений точки М от вращения колеса вокруг полюса О имеем, рис.6.22, б:
, рис. 6.22, а. Для нормального и касательного ускорений точки М от вращения колеса вокруг полюса О имеем, рис.6.22, б:
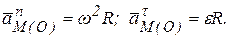
Ускорение 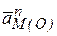 направлено от точки М к полюсу О. Ускорение
направлено от точки М к полюсу О. Ускорение 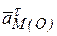 перпендикулярно отрезку ОМ и направлено в сторону дуговой стрелки e.
перпендикулярно отрезку ОМ и направлено в сторону дуговой стрелки e.
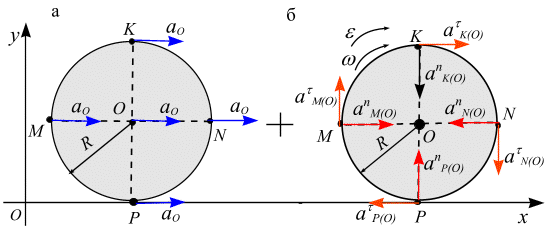
Рис. 6.22
Модуль ускорения в точке М:
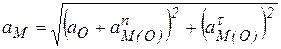
Направление вектора  показано на (рис. 6.23, а.).
показано на (рис. 6.23, а.).
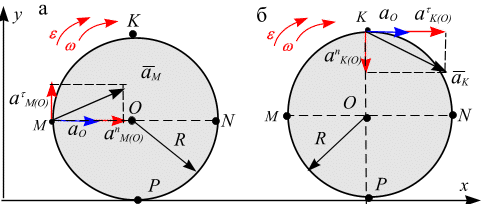
Рис. 6.23
Для точки  имеем (рис. 6.23, б):
имеем (рис. 6.23, б):
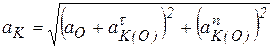 .
.
Направление вектора 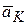 показано на рис. 6.23, б
показано на рис. 6.23, б
Для точки N имеем
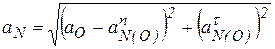 .
.
Направление вектора 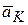 показано на рис. 6.24, а.
показано на рис. 6.24, а.
Для точки Р имеем:
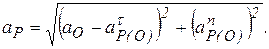 .
.
Направление вектора  показано на рис.6.24, б.
показано на рис.6.24, б.
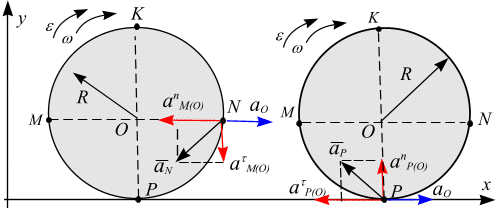
Рис. 6.24