Во многих практических задачах скорость полюса задана или ее можно вычислить. Угловая скорость вращения тела вокруг полюса часто часто неопределенна.
Теорема. В каждый момент времени при плоском движении тела, если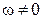 
, имеется единственная точка в плоскости его движения скорость которой равна нулю. Эту точку называют точкой мгновенного центра скоростей (МЦС). Обозначим ее Р.
Доказательство. Для доказательства этой теоремы достаточно указать способ вычисления точки МЦС. Пусть тело (П) движется плоскопараллельно. Предположим, что скорость полюса равна 
, а угловая скорость вращения тела вокруг полюса равна w (рис. 6.9). Предположим, что вращение тела вокруг полюса происходит, например, по часовой стрелке. Допустим, что мгновенный центр скоростей ( точка Р) существует. Следует ожидать, что она находится на прямой, перпендикулярной вектору скорости 
. Используем теорему о скоростях (6.3) для вычисления скорости в точке Р, рис. 6.10, получаем:
.
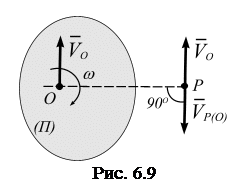
Поскольку 
, то скорость точки Р будет равна нулю, если модули этих скоростей равны между собой.
Следовательно, 
, но 
, откуда 
, тогда
.
Таким образом, точка МЦС находится на перпендикуляре к вектору скорости 
на расстоянии .
Рис. 6.10
|
Точка МЦС является единственной точкой для тела в данный момент времени. В другой момент времени точка МЦС находится уже в другой точке плоскости. Поскольку угловая скорость фигуры не зависит от выбора полюса, поэтому угловая скорость твердого тела в ее вращении вокруг точки МЦС (точка Р) равна угловой скорости w, с которой твердое тело вращается вокруг полюса О.
Если положение точки МЦС и 
известны, то, приняв точку МЦС за новый полюс (
), для любых точек тела (П), например точек А и В (рис. 6.10), скорости можно вычислить следующим образом:
,
Из полученных выражений для VА и VВ имеем
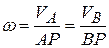
. (6.4)
| Если положение точки МЦС известно, то скорости точек тела вычисляют так же, как и в случае вращения тела в плоскости вокруг мгновенно неподвижной точки Р с угловой скоростью .
|
Следствие из теоремы о скоростях при плоском движении. Проверим справедливость общей теоремы кинематики. На рис. 6.11 построены векторы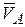 
и 
, которые составляют углы a и b соответственно с прямой АВ. Точка МЦС находится в точке Р.
Рис. 6.11
|
Опустим перпендикуляр из точки Р на прямую АВ и обозначим его через h. Тогда
.
Согласно (6.3), вычислим скорости в точках А и В через угловую скорость :
.
Вычислим длины отрезков A'A и B'B (рис. 6.11):
.
Последние равенства еще раз доказывают справедливость общей теоремы кинематики.
Следствие. Концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка.
Исходя из теоремы о скоростях при плоскопараллельном движении, имеем (рис. 6.12):
,
.
Рис. 6.12
Тогда 
и 
и, следовательно,
.
Т.к. 
и 
как противоположные стороны параллелограммов, то
.
Это соотношение показывает, что 
- отрезок прямой. Из подобия 
и 
имеем
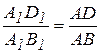, или 
и 
,
т.е. расстояния между концами скоростей пропорциональны расстояниям между соответствующими точками.