Тема 3. Оценка точности функционирования механизмов.
Расчет точности кинематических цепей механизмов заключается в определении суммарных ошибок положения и перемещения механизма или суммарной ошибки мертвого хода механизма.
Рассмотрим три метода, которые находят наиболее широкое применение на практике.
Методы определения ошибок кинематических цепей
Метод преобразованного механизма
Этот метод позволяет определить линейные зависимости ошибок положения механизмов от первичных ошибок. Он основан на идее построения схем преобразованных механизмов и планов малых перемещений, которые строятся по правилу построения планов скоростей.
Аналитическое выражение выходного параметра (перемещение ведомого звена) может бать представлено следующим образом: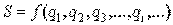 
. Чтобы установить зависимость между ошибкой механизма и первичными погрешностями, найдем полный дифференциал функции 
.
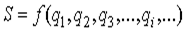или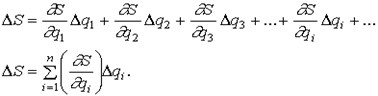 
(1)
Эта формула выражает зависимость абсолютной ошибки положения 
как линейную функцию скалярных и модулей векторных первичных ошибок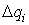 
.
Если уравнение (1) разделить на S, то получим выражение для расчета относительной ошибки положения, которое путем математических преобразований можно записать так:
.
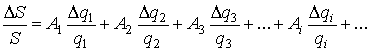Передаточное отношение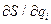 
- есть отношение малых перемещений ведомого и ведущего звеньев преобразованного механизма. Это отношение может быть найдено из плана малых перемещений преобразованного механизма.
При преобразовании механизма его ведущее звено закрепляется неподвижно, а звено, имеющее первичную ошибку, преобразуется так, чтобы остальные звенья, имеющие точные размеры, могли получить перемещения, соответствующие величине и направлению рассматриваемой первичной ошибки.
Для каждой первичной ошибки строится преобразованный механизм и план малых перемещений. Из плана находится графически, а затем определяется аналитически передаточное отношение, а затем вычисляется частичная ошибка положения механизма.
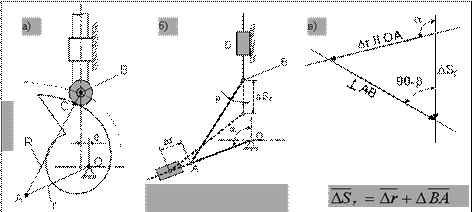
Пример1: Найти ошибку перемещения толкателя кулачкового механизма происходящую от первичной ошибки: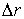 
- ошибки положения центра радиуса кривизны профиля кулачка. От кулачкового механизма переходим к эквивалентному кривошипно-шатунному, в котором высшая пара С заменена звеном АВ, оси которых расположены в центрах кривизны профиля кулачка и сферы толкателя. На рисунке (а) показан исследуемый механизм и расчетная схема преобразованного.
Преобразованный механизм и план малых перемещений, показывающий зависимость частичной ошибки положения толкателя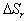 
от первичной ошибки 
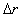, приведены на рисунках (б и в). Для плана малых перемещений (см. рис 2.4, а) запишем теорему синусов:
.
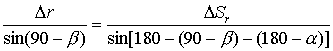или 
,
затем определим частичную ошибку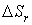 
:
(2).
Для того чтобы выражение (2) сделать функцией одного аргумента, например, угла поворота кривошипа a, выразим тригонометрические функции угла b через геометрические параметры механизма и угол a (см рис. 2.3).
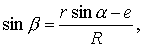
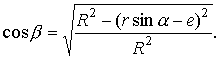
После преобразований будем иметь:
.
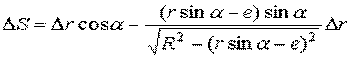Подобным образом можно определять частичные и суммарные ошибки других типов механизмов.