Этот метод широко применяется если известна аналитическая функциональная связь между ведущими и ведомыми звеньями. Для механизмов, состоящих из рычагов, гибких связей и фрикционных колес, вводится понятие об относительной радиальной ошибке.
Относительной радиальной ошибкой называется отношение абсолютной ошибки радиального размера Dr к номинальной величине этого размера r.
Определим ошибку перемещения механизма, показанного на рисунке.
Чтобы выразить ошибку перемещения механизма DS6 через ошибки длин Dri всех плеч ri рычагов, напишем общее уравнение движения механизма, продифференцируем его в частных производных и заменим дифференциалы малыми приращениями:
 .
.
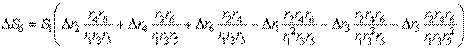
В этом уравнении члены, содержащие ошибки ведомых плеч, умножим и разделим на размеры соответствующих плеч, и после преобразования получим формулу для определения ошибки перемещения механизма
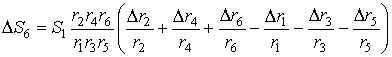 .
.
Из полученной формулы видно, что в последовательной передаче все относительные ошибки звеньев имеют постоянное передаточное отношение, так как умножаются на одинаковый множитель.
Относительная ошибка перемещения механизма равна DS6/S6 или
 ,
,
где по i суммируются относительные ошибки ведомых плеч, а по j ведущих.
Для зубчатых колес относительная радиальная ошибка практического значения не имеет, так как сохраняет свои особенности лишь при углах поворота колеса меньших, чем угловой шаг t = 2p/z.
Рассмотрим применение метода относительных ошибок для расчета суммарной погрешности кровошипно-шатунного механизма (см. рис. (б) в первом методе). Ведомое звено, ползун, совершает поступательное движение вдоль оси OY. Уравнение движения точки В, в функции угла поворота кривошипа a, имеет вид:

Для определения частичной ошибки DSr, вызванной погрешностью длины кривошипа, вычислим частный дифференциал полученной функции по переменной r

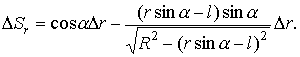
и сравним полученные формулы.
1.3 Метод планов малых перемещений

Это метод, позволяющий строить единый план малых перемещений для определения ошибки положения ведомого звена, которая вызвана ошибками всех звеньев механизм. При этом используется кинематическая схема механизма и принимается допущение, согласно которому ошибки размеров звеньев считаются настолько малыми, что направления звеньев реального и теоретического механизма совпадают.
Точка В любого звена АВ (рис. а) может иметь два дефективных перемещения: нормальное перемещение ` SnAB, известное по величине и направлению, равное заданной ошибке длины звена, и тангенциальное перемещение `StAB ^ BA, известное только по направлению, которое является следствием ошибки Dj в угловом положении звена.
План малых перемещений имеет некоторое сходство с планом ускорений. Перемещение каждой точки звена относительно своего теоретического положения рассматривается как сумма переносного поступательного перемещения (`SA) всего звена вместе с точкой А (перемещение которой известно) и относительного перемещения ` SBA точки В относительно точки А.
Для схем, приведенных на рисунке, перемещения одной точки можно выразить через перемещения других точек посредством векторных уравнений:
для рис. а ` SB = `SA + `SBA = `SA + `SnBA + `StBA;
для рис. б ` SA1 = `SA0 + `SA1A0;
для рис. в ` SA3 = `SA2 + `SA3A2 = `SB + `StA3B;
для рис. г ` SD =`SA +`SnDA +`StDA =`SB +`SnDB +`StDB.
В кулисном механизме расстояние А3В рассматривается как теоретическое, поэтому принимают SnA3B = 0 и не записывают его в первую часть уравнения.
При построении плана малых перемещений «последний» элемент кинематической пары стойки, которым стойка связана с ведомым звеном механизма, считают совпадающим со своим теоретическим положением. Нормальные перемещения осей шарниров и направляющих других кинематических пар механизма считаются заданными по отношению к системе координат, связанной с «последним» элементом стойки. Перемещения точек звеньев относительно стойки откладываются от полюса плана р.
Пример. На рис. 2.7, д, е показаны схема механизма прибора и построение плана малых перемещений. Считаем, что шарнир О совпадает со своим теоретическим положением. Заданы по величине и направлению первичные ошибки: перемещение направляющей ползуна ` SA и нормальные перемещения ` SnBA;` SnBO. От полюса плана р откладываются перемещения точек механизма относительно стойки.
Для определения перемещения точки В решаем графически векторные уравнения ` SB= ` SA+ ` SnBA+ ` StBA= ` SnBO+ ` StBO. При этом` SnBA || BA; ` StBA ^ BA; ` SnBO || BO; ` StBO ^ BO. В пересечении направлений ` StBA и ` StBO находим точку b и перемещение ` SB = p`b.