Многообразие побудительных мотивов деятельности отдельных экономических субъектов и постоянное изменение внешней экономической среды, вызывающее нестабильность их предпочтений во времени, малый объем доступных эмпирических данных – все это характеризует проблему потребительского выбора как одну из ключевых проблем современной микроэкономики. Одним из направлений исследований в данной сфере является так называемая «экспериментальная микроэкономика », изучающая поведение потребителей на основе статистических и экспериментальных данных. Анализ известных результатов микроэкономических экспериментов позволяет отметить два характерных момента: классические теории выбора часто не выдерживают эмпирической проверки, а различные эксперименты выявляют различное поведение потребителей, не согласующееся с ожидаемым поведением, диктуемым известными теориями. В частности, в моделях динамического (межвременного) выбора важнейшим новым феноменом является гипотеза гиперболического дисконтирования. [1]
Теория межвременного выбора всегда привлекала к себе пристальное внимание со стороны экономистов. На то были и остаются серьезные основания. Решения, принимаемые индивидами и включающие в себя соизмерение понесенных издержек и получаемых выгод, которые относились бы к различным периодам времени, являются центральными в области исследования сбережений и инвестиций, потребительского поведения, а в конечном счете проблем, связанных с общественным благосостоянием той или иной нации. Поэтому вовсе не случайно, что экономисты прошлого уделяли серьезное внимание проблеме теоретического анализа факторов, влияющих на поведение экономических субъектов в ситуациях принятия решений, когда последствия, а точнее, результаты действий становятся известными спустя определенное время.
Неоклассическая экономическая теория также не оставила без внимания данную проблему. Своеобразным фундаментом, теоретической основой для последующих более чем полувековых исследований в этой области стала модель дисконтированной полезности, предложенная П. Самуэльсоном в 1937 году и получившая аксиоматическую трактовку в работах Т. Купманса[2].
В своей наиболее упрощенной форме модель определяет межвременные предпочтения лица, принимающего решение, между различными конфигурациями потребительских планов (сt,..., сТ). При условии соблюдения ряда обычных предпосылок (полнота, транзитивность, непрерывность) эти предпочтения могут быть представлены с помощью межвременной функции полезности U t(сt,..., сТ) в следующей функциональной форме:
 , где
, где  .
.
В данной формулировке u(ct+k) обычно интерпретируется как количественная функция полезности индивида — его благосостояние в момент времени t + k, а D(k) — это функция дисконтирования индивида, другими словами тот относительный вес, который он приписывает в момент времени t своему уровню благосостояния в период t + k. Параметр r в данном случае, это — чистый показатель временного предпочтения индивида (ставка дисконтирования).
Если рассматривается непрерывный промежуток времени от t до T, то межвременная функция полезности представляется в интегральной форме
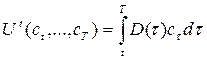 , где
, где 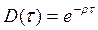 ,
,
величина ρ представляет собой непрерывную ставку дисконта, связанную с r равенствами
 ,
,  .
.
Таким образом, в упрощенной модели П. Самуэльсона все психологические факторы, так или иначе обсуждавшиеся в произведениях экономистов предыдущего столетия в ходе анализа проблем межвременного выбора, были сведены к единственному параметру, ставке дисконтирования.
С течением времени модель дисконтированной полезности нашла применение в таких разнообразных разделах экономики, как теория сбережений, предложение труда, оценка инвестиционных проектов с точки зрения рисков и доходов и др. Данная модель обеспечила простую, но мощную аналитическую схему для анализа широкого спектра экономических решений, последствия которых не известны в момент совершения действий. Такая до крайности простая и понятная модель вошла во все учебники финансовой математики и стала фундаментом банковского дела, оценочного бизнеса, а зачастую и государственной политики, хотя совершенно не соответствовала эмпирическим данным.
Справедливости ради следует отметить, что, предлагая данную модель, П.Самуэльсон ясно давал понять, что ее статус в качестве нормативного и дескриптивного инструмента исследования экономических явлений представляется довольно проблематичным. В то же время целью работы Т. Купманса было лишь продемонстрировать, что при соблюдении некоторых четко определенных условий, аксиом, которые, возможно, являются нереалистичными, индивиды логически принуждаются к принятию положительных временных предпочтений (ставки дисконтирования), при этом никаких претензий по поводу адекватности модели дисконтированной полезности явлениям и фактам реального мира не высказывалось. Несмотря на это, мнение самого Т.Купманса, было, по большому счету, забыто, а его аксиоматизация способствовала популярности этой теории и повышению ее статуса в экономической науке.
В результате большого количества экспериментальных и эмпирических исследований экономического поведения индивидов, которые были проведены по данной проблеме на протяжении последних двух десятилетий, учеными были обнаружены и задокументированы различные несоответствия и аномалии модели дисконтированной полезности, что привело к вопросу о неадекватности этой модели как дескриптивного инструмента анализа поведения индивидов в ситуациях межвременного выбора. Анализ аномалий данной модели показал необходимость построения новых моделей, учитывающих эти недостатки и являющихся надстройками над моделью дисконтированной полезности. Подробный обзор этих моделей дается в статьях, указанных в приведенной выше сноске.
Альтернативой модели дисконтированной полезности является модель гиперболического дисконтирования, предполагающая убывающую ставку межвременных предпочтений. Гиперболическое дисконтирование считается экспериментально подтвержденной формой расчета в модели разности предпочтений, которые экономический субъект имеет в потреблении сейчас над потреблением в будущем. Через t периодов дисконтирование производится множителем

где a, g ― скалярные вещественные параметры, большие 0. Эта формулировка дана в работе Харриса и Лейбзона 2001 г., которая в свою очередь ссылается на работы Эйнсли 1992 г. и Ловенштейна и Прелека 1992 г.[3]
Модель гиперболического дисконтирования в последние годы начинает появляться в областях финансовых исследований: пенсионные сбережения, использование кредитных карт и т.д.
Гиперболическое дисконтирование более релевантно человеческой психологии, хотя и менее удобно в расчетах, чем общепринятое экспоненциальное дисконтирование с постоянной ставкой дисконта, так как содержит два параметра и, кроме того, прогнозирует решения экономических субъектов как динамически несостоятельные, т.е. не постоянные во времени. Имеется в виду конфликт между оптимальным планом на будущее с позиции «сегодняшней» перспективы и оптимальным планом на будущее с позиции «завтрашней» перспективы.
В целях упрощения расчетов Фелпсом и Поллаком была введена модель квази-гиперболического дисконтирования с дисконтирующим множителем, отражающая основной смысл гиперболического дисконтирования:
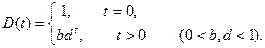
Данная модель предполагает уменьшающуюся ставку дисконтирования между настоящим периодом и следующим, но постоянную ставку дисконтирования для всех остальных периодов; кроме того, она включает многие качественные положения гиперболического дисконтирования, найденные экспериментально. Функция дисконтирования D (t) в данной модели существенно дискретна и может быть выражена последовательностью значений {1, bd, bd 2, bd 3, …}[4].
Модель гиперболического дисконтирования основывается на трех основных экспериментах в отношении межвременного выбора (подробный обзор дается в работах, уже указанных ранее).
Первое предположение гиперболического дисконтирования: при оценке сегодняшнего потребления ставка дисконтирования убывает по мере возрастания длительности периодов, проверено экспериментом Талера (США). Респондентов просили указать, какая сумма через 1 месяц/1 год/10 лет сделает их безразличными к получению $15 сейчас. Медианы ответов ($20/$50/$100) определили среднюю (годовую) ставку дисконтирования в размере 3,45; 1,20; 0,19 соответственно. Многочисленные повторения данного эксперимента подтвердили значимость его результата, хотя и с различными скоростями убывания, что соответствует наличию в коэффициенте гиперболического дисконтирования двух параметров. Например, Давыдов и Тарасов в марте 2003 г. повторили эксперимент со студентами Дальневосточного государственного университета; результаты приведены ниже.
| Период времени | 1 месяц | 1 год | 2 года | 10 лет |
| Медиана | ||||
| Среднее | 4669.29 | 2521.44 | 1392.08 | 540.17 |
| Ставка дисконтирования, соответствующая медиане | 8.32 | 1.90 | 1.50 | 0.46 |
| Ставка дисконтирования, соответствующая среднему | 9.14 | 1.38 | 0.98 | 0.29 |
Нет никаких сомнений, что параметры гиперболического дисконтирования зависят от множества экономических факторов ― уровень странового риска и т.д., а для физических лиц ― уровень жизни в регионе, уровень потребления и т.д.
Вторая группа экспериментов по проверке значимости модели гиперболического дисконтирования относилась к выявлению предпочтения между двумя «задержанными премиями». Рядом экономистов экспериментально показано, что предпочтения экономических субъектов могут «менять направление » при приближении премий во времени: например, предпочтение потребителем суммы в $110 через 31 день сумме в $100 через 30 дней, но предпочтение тем же потребителем суммы в $100 сейчас по сравнению со $110 завтра.
Третий эксперимент направлен на выявление предпочтения возрастающей либо убывающей последовательности доходов. Данный эксперимент был проведен в 1991 г. Ловенштейном и Сикерманом. Из двух схем получения дохода: убывающей ($27000, $26000, $25000, $24000, $23000) и возрастающей ($23000, $24000, $25000, $26000, $27000), респонденты в подавляющем большинстве предпочли возрастающую схему. Заметим, что сумма дохода без учета дисконтирования для обеих схем денежного потока была равной, а с учетом дисконтирования по постоянной ставке убывающая последовательность дохода предоставляет большие возможности потребления (и реинвестирования).
Неадекватность классической модели дисконтирования с постоянной ставкой дисконта реальным экономическим задачам иллюстрирует и ряд других обнаруженных феноменов, относящихся по своему содержанию к различным областям и сферам экономической деятельности (финансовые рынки, страхование, потребительское поведение). Среди них следующие[5].
1. Головоломка о доходности капитала (equity premium puzzle) — слишком высокая доходность денежных средств, вложенных в акции по сравнению с доходностью государственных облигаций или активов, не сопряженных с риском.
2. Эффект размещения (disposition effect) — чрезмерно долгое владение проигрышными акциями, то есть ценными бумагами, падающими в цене, и в то же время слишком быстрая продажа акций, растущих в стоимости.
3. Асимметричные ценовые эластичности — покупки людей являются более чувствительными к увеличению цены по сравнению с одинаковым уменьшением, снижением последней.
4. Невосприимчивость к плохим новостям, касающимся располагаемого дохода, — потребители не снижают достигнутый уровень потребления после поступления отрицательной, неблагоприятной информации о собственных доходах.
5. Переоценка возможных потерь и выгод — приобретение потребителями завышенных в цене страховых полисов от нежелательных исходов, а также лотерейных билетов, при том, что ожидаемая полезность выигрыша, как правило, ниже стоимости самого билета.
Наибольшее теоретическое и практическое значение среди вышеперечисленных феноменов представляет головоломка о доходности капитала. Авторами данного феномена являются Р. Мехра и лауреат Нобелевской премии по экономике 2004 г. Э. Прескотт[6]. Дж. Зигель и Р. Талер в своей работе 1997 г.[7] приводят конкретный пример из реальной жизни:
"Предположим, что ваша бабушка располагала определенной свободной суммой денег в конце 1925 года и, поступая в соответствии с гипотезой рациональных ожиданий, а также предвидя ваше появление на этот свет, решила передать вам по наследству 1 тысячу долларов США. Естественно, что, так как вы еще не родились, она решила инвестировать деньги и, опасаясь спекулятивного бума, набиравшего обороты как раз в тот самый период, вложила их в государственные казначейские обязательства, попросту облигации (Treasure bills), в которых они хранились до 31 декабря 1995 года. На эту дату их общая стоимость составила 12 720 долл. Представьте себе при этом, что, вместо того чтобы вложить деньги в облигации, ваша бабушка инвестировала их в портфель ценных бумаг, взвешенный по стоимости наиболее ликвидных акций на рынке. При подобном варианте развития событий ваша прибыль на момент окончания 1995 года составила бы 842 000 долл. или, что то же самое, была бы больше в 66 раз."
Подобная разница в доходности различных вариантов инвестирования денег является чрезвычайно большой и не может быть объяснена в категориях стандартных экономических моделей. (Не может быть объяснено, почему до сих пор существуют и пользуются спросом безрисковые ценные бумаги.)
Новые модели вызывают определенные критические замечания со стороны экономистов. Например, А. Рубинштейн[8] считает, что существует множество различных функциональных форм, которые можно было бы принять в качестве модели дисконтирования при убывающем коэффициенте дисконтирования, а те же эксперименты, которые показывают отклонения от модели экспоненциального дисконтирования, могут служить и для демонстрации недостатков гиперболического дисконтирования.
Зачем вообще применяется дисконтирование? Традиционный ответ заключается в том, что будущие платежи сопровождаются риском обесценения, невыплаты или неполной выплаты. Приняв в качестве (непрерывной) ставки дисконтирования ρ уровень риска, в момент времени t равный отношению 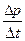 вероятности Δ p неплатежа в интервале между моментами t и t +Δ t, получим, если данный случайный процесс пуассонов – т.е. уровень риска не зависит от времени t – что стоимость будущего платежа V в момент времени T имеет в настоящий момент ценность
вероятности Δ p неплатежа в интервале между моментами t и t +Δ t, получим, если данный случайный процесс пуассонов – т.е. уровень риска не зависит от времени t – что стоимость будущего платежа V в момент времени T имеет в настоящий момент ценность 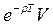 . Если же уровень риска ρ = ρ (t) меняется с удалением момента времени от настоящего во все более глубокое будущее (в сторону увеличения) или же увеличивается неопределенность в оценке данного параметра, требуется, как считают Дасгупта и Маскин[9], новая модель дисконтирования, первым кандидатом на роль которой является гиперболическое дисконтирование. В этой модели (непрерывная) ставка дисконтирования уменьшается с увеличением горизонта:
. Если же уровень риска ρ = ρ (t) меняется с удалением момента времени от настоящего во все более глубокое будущее (в сторону увеличения) или же увеличивается неопределенность в оценке данного параметра, требуется, как считают Дасгупта и Маскин[9], новая модель дисконтирования, первым кандидатом на роль которой является гиперболическое дисконтирование. В этой модели (непрерывная) ставка дисконтирования уменьшается с увеличением горизонта:
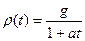 .
.
Гиперболическая ставка дисконтирования вначале равна g, но затем уменьшается ― в пределе до нуля.
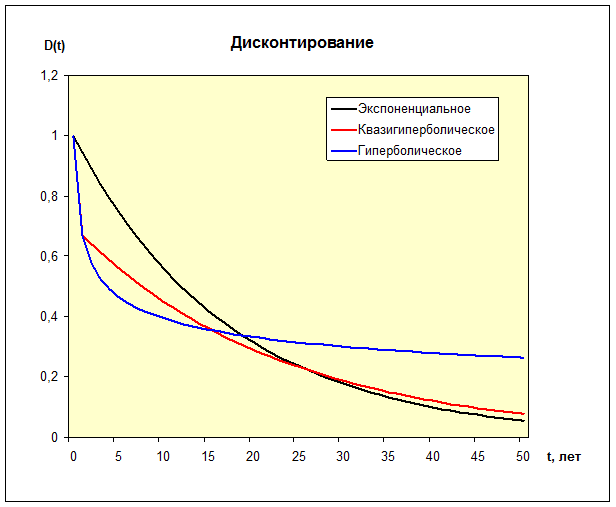
На следующем рисунке изображены графики функций дисконтирования:
1) экспоненциальной 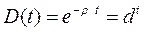 , при d = 0,944;
, при d = 0,944;
2) гиперболической  , при a = 4 и g = 1;
, при a = 4 и g = 1;
3) квазигиперболической {1, bd, bd 2, bd 3, …}, при b = 0,7 и d = 0,957.
[1] Shane F., Loewenstein G. and O’Donoghue T. Time Discounting and Time Preference: A Critical Review // Journal of Economic Literature. Vol. XL (June 2002).
Loewenstein G., Prelec D. Anomalies in Intertemporal Choice: Evidence and an Interpretation // Quarterly Journal of Economics. 107:2. Р.573-597 (1992).
Laibson D. Golden Eggs and Hyperbolic Discounting // Quarterly Journal of Economics. Vol. 62, No. 2. 1997. PР.443-478.
Давыдов Д.В., Тарасов А.А. Модели поведения потребителей: экспериментальная проверка в региональных условиях // Управление в социально-экономических системах. 2003. №2(6). c. 57-66.
[2] Samuelson P. A Note on Measurement of Utility // Review of Economic Studies. 1937. Vol. 4. P. 155-161; Koopmans T. C. Stationary Ordinal Utility and Impatience // Econometrica. 1960. Vol. 28. P. 287-309.
[3] Harris C., Laibson D. Hyperbolic discounting and consumption. 2001. (www.iies.su.se/nobel/laibsonstockholm.pdf); Ainslie G. Picoeconomics. Cambridge: Cambridge University Press, 1992; Loewenstein G., Prelec D. – см. ссылку выше. Ловенштейн и Прелек предложили аксиоматический вывод функции обобщенного гиперболического дисконтирования. Впервые, как указывают Харрис и Лейбзон, понятие гиперболического дисконтирования появилось в работе: Chung Shin-Ho, Herrnstein R.J. Relative and Absolute Strengths of Response as a Function of Frequency of Reinforcement // Journal of the Experimental Analysis of Animal Behavior, 4, 1961, pp. 267-272. В первых работах по гиперболическому дисконтирования исследовался психологический аспект межвременного предпочтения в процессе потребления у животных и человека. Обзор этих работ дан в книге Эйнсли. Отметим, что сначала рассматривались специальные случаи функции гиперболического дисконтирования 1/ t и 1/(1+ at).
[4] Laibson D. – см. ссылку выше; Phelps E.S., Pollak R.A. On Second-best National Saving and Game-Equilibrium Growth // Review of Economic Studies. 35, 1968. PP. 185-199.
[5] Camerer C. F. Prospect Theory in the Wild: Evidence from the Field // Social Science Working Paper 1037. May, 1998. Division of the Humanities and Social Sciences California Institute of Technology. In book: Kahneman D., Tversky A. Choices, Values, and Frames. Cambridge, 2000. PP. 288-300.
[6] Mehra R., Prescott E. C. The Equity Premium: A Puzzle // Journal of Monetary Economics. March, 1985. Vol. 15. PP. 145-162.
[7] Siegel J.J., Thaler R.H. Anomalies: The Equity Premium Puzzle // The Journal of Economic Perspective. Winter, 1997. Vol. 11, N 1. PP. 191-200.
[8] Rubinstein A. Is It "Economics and Psychology"?: The Case of Hyperbolic Discounting. (https://www.princeton.edu/~ariel/).
[9] Dasgupta P., Maskin E. Uncertainty and Hyperbolic Discounting. Princeton, 2004.