1. Теплофизические свойства криопродуктов: Учебное пособие для вузов / Л.А. Акулов, Е.И. Борзенко, В.Н. Новотельнов, А.В. Зайцев. – СПб.: Политехника, 2001. – 243 с.: ил.
2. Физический энциклопедический словарь/ Гл. ред. А.М. Прохоров. Ред. кол. Д.А. Алексеев, А.М. Бонч-Бруевич, А.С. Боровик-Романов и др. − Сов. Энциклопедия, 1983. – 928 с., ил., 2 л. цв. ил.
3. Архаров А.М. и др. Криогенные системы: Учебник для студентов вузов по специальности «Техника и физика низких температур»: В 2 т. Т.1. Основы теории и расчёта / А.М. Архаров, И.В. Марфенина, Е.И. Микулин. – 3-е изд., перераб. и доп. – М.: Машиностроение, 1996. – 576 с.: ил.
4. Диканова Л.Ф. Криогенная техника. Методические указания к практическим работам для студентов специальности 070200 «Техника и физика низких температур». – Владивосток: Дальрыбвтуз, 1999. – 55 с.
ПРИЛОЖЕНИЕ 1
П1.1. Требования к оформлению и содержанию отчёта
Отчет по практической работе выполняется на листах формата А4 рукописным или машинописным способами, аккуратно и грамотно.
Отчет должен содержать:
– титульный лист;
– цель работы;
– принципиальную схему и цикл воздухоразделительной установки, краткое описание принципа работы воздухоразделительной установки, таблицу параметров точек цикла, необходимые расчеты;
– таблицу анализа циклов, их сравнение и выводы.
Изложение содержания отчёта должно быть логически последовательным, кратким и соответствовать ГОСТ 2.105-79. Сокращение слов в тексте, за исключением общепринятых в русском языке, не допускается.
Результаты экспериментов оформляют в виде таблиц. Над правым верхним углом помещают надпись "Таблица" с указанием её порядкового номера, ниже − название таблицы.
Значения символов и числовых коэффициентов расшифровывают непосредственно под формулой в той последовательности, в какой они приведены в ней, например,
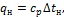
где 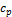 − теплоемкость воздуха, кДж/(кг К);
− теплоемкость воздуха, кДж/(кг К); 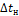 − разность температур на теплом конце теплообменника.
− разность температур на теплом конце теплообменника.
П1.2. Пример оформления титульного листа
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ
Федеральное государственное бюджетное учреждение
высшего образования

| «Дальневосточный государственный технический рыбохозяйственный университет» |
Кафедра «Холодильной техники, кондиционирования воздуха и теплотехники»
ОТЧЕТ
по практической работе №_____
___________________________________________________
(наименование)
| Выполнил: Студент группы ____________ Ф.И.О. «__» __________ 201__ г. | Принял: Преподаватель ___________ Ф.И.О. «__» __________ 201__ г |
Владивосток
П 1.3. Аппроксимирующие уравнения
экспериментальных данных для воздуха
Уравнение состояния
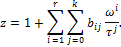
| (П.1) |
где 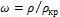 (
(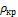 − критическая плотность);
− критическая плотность); 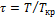 – приведенная температура (
– приведенная температура (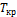 − критическая температура);
− критическая температура); 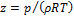 .
.
Коэффициенты разложения уравнения (П.1) представлены в табл.
П 1.1.
Таблица П1.1.
Коэффициенты разложения 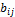 уравнения (1.1) для воздуха
уравнения (1.1) для воздуха
| i | Значения 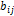 при j при j
| |||||||||||||||||
| 0,366812 | -0,252712 | -2,84986 | 3,60179 | -3,18665 | 1,54029 | -0,260953 | -0,0391073 | |||||||||||
| 0,140979 | -0,0724337 | 0,780803 | -0,143512 | 0,633134 | -0,891012 | 0,0582531 | 0,0172908 | |||||||||||
| -0,0790202 | -0,213427 | -1,25167 | -0,16497 | 0,684822 | 0,221185 | 0,0634056 | ||||||||||||
| 0,313247 | 0,885714 | 0,634585 | -0,162912 | -0,217973 | 0,0925251 | 0,000893863 | ||||||||||||
| -0,444978 | -0,734544 | 0,0199522 | -0,176007 | -0,0998455 | -0,0620965 | |||||||||||||
| 0,28578 | 0,258413 | 0,0749790 | 0,0859487 | -0,000884071 | ||||||||||||||
| -0,0636588 | -0,105811 | -0,0345172 | 0,0429817 | 0,00631385 | ||||||||||||||
| 0,000116375 | 0,0361900 | -0,0195095 | -0,00379583 | |||||||||||||||
По сравнению с другими видами уравнений состояния реального газа достоинством усредненного уравнения (П.1) является то, что оно позволяет определять термодинамические параметры криопродуктов как в газообразном, так и в жидком состоянии в широком интервале изменения основных параметров.
Рекомендуемые интервалы применения уравнения (П.1) для воздуха:
давление 0,1…100 МПа;
температура 70…1500К.
Средняя квадратичная погрешность при аппроксимации использованных опытных данных по плотности 0,11%.
Давление насыщенных паров криопродуктов рассчитывают по интерполяционному уравнению /1/
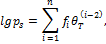
| (П.2) |
где 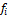 – коэффициенты уравнения, значения которых для воздуха приведены в таблице П1.2, там же даны пределы применимости уравнения 1.2;
– коэффициенты уравнения, значения которых для воздуха приведены в таблице П1.2, там же даны пределы применимости уравнения 1.2; 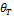 − относительная температура,
− относительная температура, 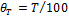 ;
; 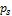 − давление насыщенных паров криопродукта, МПа.
− давление насыщенных паров криопродукта, МПа.
Таблица П1.2
Значения коэффициентов 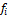 уравнения (П.2) для воздуха
уравнения (П.2) для воздуха
| f 1 | f 2 | f 3 | f 4 | f 5 | Интервал температур применения уравнения | |
| кипение | -3,92905 | 6,42564 | -5,29158 | 3,42776 | -0,81182 | 60-132 |
| конденсация | -3,94049 | 5,18794 | -2,59029 | 1,30894 | -0,21794 |
Калорические уравнения, связывающие энтальпию, энтропию и теплоемкость с давлением и температурой, могут быть получены на основе обобщения экспериментальных данных, либо путем интегрирования p-r-T −зависимости. При использовании второго пути /1/, и для определения значения энтальпии предлагается формула
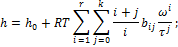
| (П.3) |
энтропии –
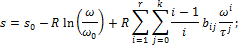
| (П.4) |
изобарной теплоемкости
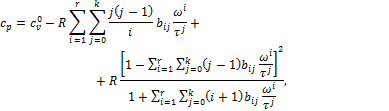
| (П.5) |
где 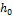 ,
, 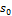 ,
, 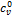 − энтальпия, энтропия и изохорная теплоемкость в идеальном газовом состоянии.
− энтальпия, энтропия и изохорная теплоемкость в идеальном газовом состоянии.
Энтальпию 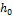 и энтропию
и энтропию 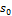 определяют из соотношений /1/:
определяют из соотношений /1/:
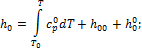
| (П.6) |
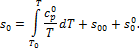
| (П.7) |
Здесь 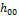 и
и 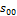 − энтальпия и энтропия при температуре
− энтальпия и энтропия при температуре 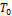 ;
; 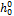 − теплота сублимации при
− теплота сублимации при 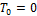 К;
К; 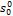 − константа. Значения констант уравнений (П.3) − (П.7) приведены в табл. П1.3.
− константа. Значения констант уравнений (П.3) − (П.7) приведены в табл. П1.3.
Значение изобарной теплоемкости в идеальном газовом состоянии рассчитывается с помощью полинома /1/
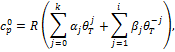
| (П.8) |
где 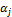 ,
, 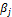 − коэффициенты полинома (табл. П1.4).
− коэффициенты полинома (табл. П1.4).
Таблица П1.3
Параметры воздуха и константы уравнений (П.3) − (П.7)
| Коэффициент сжимаемости zкр | Теплота сублимации 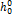 при при 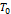 , кДж/кг , кДж/кг
| Энтальпия 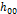 при при 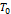 ,кДж/кг ,кДж/кг
| Энтропия 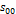 при при 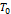 , кДж/(кгК) , кДж/(кгК)
| Константа 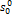 при при 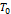 , кДж/(кгК) , кДж/(кгК)
| Фактор ацентричности w’ |
| 0,291 | 253,40 | 3,48115 | 20,0824 | 0,0 | -0,0094 |
Таблица П1.4
Значения коэффициентов полинома (П.8) для воздуха
| j | 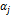
| 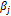
|
| 6,61738 | ||
| -1,05885 | -5,49169 | |
| 0,20165 | 5,85171 | |
| -0,0196930 | -3,72865 | |
| 0,00106460 | 1,33981 | |
| -0,0000303284 | -0,233758 | |
| 0,000000355861 | 0,0125718 |
ПРИЛОЖЕНИЕ П2