ЧЕРТЕЖИ СТАНДАРТНЫХ ДЕТАЛЕЙ, ЗУБЧАТЫХ КОЛЕС, ЗУБЧАТЫХ ПЕРЕДАЧ И ПРУЖИН 2 глава

В третьей части таблицы параметров может быть указан размер диаметра дели­тельной окружности и другие справочные данные (на рис. 261 их нет).

Выполнение эскиза зубчатого колеса. Последовательность выполнения эскизов деталей изложена в § 56 гл. V!. Здесь дополнительно рассмотрим лишь то, что относится к зубчатым колесам.

Общий порядок выполнения эскиза зуб-

Рис. 262. Схема контроля разме­ра общей нормали

чатого колеса следующий: определяют мо­дуль и число зубьев; подсчитывают основ­ные параметры зубчатого колеса; выпол­няют эскиз.

Определение модуля и числа зубьев. При подсчете числа зубьев обычно поме­чают мелом один из зубьев и от него по окружности подсчитывают их ' число. Пусть оно равно 68.

Для определения модуля надо восполь­зоваться приведенной ранее для подсчета диаметра окружности вершин формулой %л =?п(2 + 2), откуда ги=&/(2 + 2); число зубьев нам известно.

Диаметр окружности вершин измеряют штангенциркулем, как показано на рис. 263. Пусть он равен 203 мм.

Подставив в формулу /я=л./(2+2) по­лученные данные, имеем /я = 203/(68 + + 2)=203/70=2,9.

Значение модуля сопоставляют со стан­дартными, приведенными в § 62 в со­ответствии с ГОСТ 9563—60, и выбирают ближайший, т. е. 3 мм.

Ошибка на ОД мм может получиться в результате неточного обмера и износа колеса.

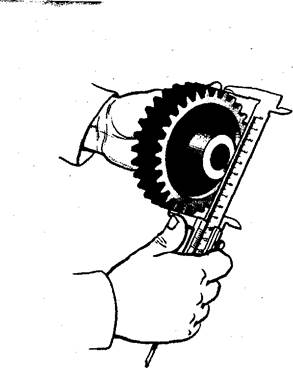Рис. 263. Измерение диаметра окружности вершин зубьев зубчатого колеса

Итак, в нашем примере число зубьев 2=68, а модуль т = 3.

Подсчет основных параметров зубчато­го колеса. Чтобы условно изобразить зуб­чатый венец, определяют диаметр трех окружностей.

Если при подсчете модуля результат несколько отличался от стандартного нследствие износа поверхности вершин, то гогда необходимо определить диаметр ок­ружности вершин, т. е. наружный диаметр колеса. Подставив в формулу %а=т(2 + 2) число зубьев и модуль, получим = 3(68 + 2)=210 мм.

Диаметр делительной окружности под­считывают по формуле б? =?Л2 = 3-68 = = 204 мм.

Диаметр окружности впадин подсчиты­вают по формуле ф=%—2,5т = 204 — -2,5-3=196,5 мм.

Из этих трех размеров на эскизе про­ставляют, как было указано, лишь диа­метр окружности вершин.

Остальные размеры берут с натуры. Когда выполняют чертеж колеса, не имея натуры, эти размеры подсчитывают по со­отношениям, приведенным в табл. 6. При этом диаметр вала выбирают в соответст­вии с ГОСТ 6636—69, а размеры шпо­ночного паза — в зависимости от диамет­ра вала по ГОСТ 23360— 78.

На рабочих чертежах поля допусков и предельных отклонений шпоночных па­зов записывают по следующему образцу, например: 10М9 (-о.азб) или 10Р9 (-о.озб) — паз вала; Ю/:9 (±0,018)—паз втулки.

Выполнение эскиза. Эскиз выполняют в соответствии с определенными размера­ми. Зарисовывают вид слева, проводя три концентрические окружности (рис. 264, а), диаметры которых в нашем примере ла = = 210 мм, %=204 мм, <%;= 196,4 мм. За­рисовывают фронтальный разрез, опреде­ляя границы зубьев с помощью линий связи (рис. 264, а).

Зарисовывают на виде слева и разрезе отверстие для вала, шпоночный паз и дру­гие конструктивные элементы. Затем обво­дят окружности вершин сплошной основ­ной линией, делительную — штрихпун- ктирной, а впадин — сплошной тонкой линией (рис. 264,6). Заштриховывают разрез колеса, оставляя незаштрихован- ными зубья, на изображении которых про­водят штрихпунктирные линии, соответ­ствующие делительной окружности. Нано-

Рис. 264. Последовательность выполнения эскиза цилиндрического зубчатого колеса

 

сят размерные линии и размерные числа, обозначение шероховатости поверхностей, предельные отклонения формы и располо­жения поверхностей, заполняют • таблицу параметров, записывают технические тре­бования, заполняют основную надпись. Чертеж зубчатого колеса выполняют ана­логично.

Когда выполняют чертеж цилиндриче­ского зубчатого сектора, т. е. колеса, име­ющего неполный зубчатый венец, то, в таб­лице параметров помещают данные, ха­рактеризующие полное цилиндрическое колесо. Число зубьев указывают тоже для полной окружности. Это делается для вы­бора зуборезного инструмента, который маркируется модулем и числом зубьев. Фактическое число зубьев в секторе ука­зывают в таблице параметров в третьей, справочной ее части.

К.

Особенности чертежей цилиндрических колес с косыми зубьями. Для достижения более плавной передачи вращательного движения применяют зубчатые колеса не с прямыми, а с косыми или шевронными зубьями. Колесо с косыми зубьями нари­совано на рис. 259л6. Шевронные колеса можно представить себе как составленные из двух колес с разным направлением зубьев — одно с правым, другое с левым направлением (см. рис. 259, а).

Для колёс с косыми зубьями различают нормальный модуль (Я!п) и торцовый (?Яз). Нормальный модуль определяют по так называемому нормальному сечению зуба, которое получается сечением плоско- сти,.перпендикулярной длине зуба. Торцо­вый модуль определяют по плоскости тор­ца колеса, т. е. как и у колес с прямым направлением зубьев.

Если угол наклона зуба к оси колеса равен р, то нормальный модуль определя­ют через торцовый по формуле /н„ = = соз

Диаметр делительной окружности коле­са с косыми зубьями определяют по фор­муле Й = 2n_s- или по формуле <% = = (%-/и,,)/с<мр, если ■ дан нормальный мо­дуль.

Высота головки зуба (й„) у косозубых колес равна нормальному модулю (Аз = *=?Яд), а высота ножки зуба равна [,2/п„ иормального модуля (Д;=!,2?Пл)<

Диаметр окружности вершин у цилин­дрических косозубых колес подсчитывают по формуле йа=й + 2тя, а диаметр ок­ружности впадин — по формуле й?=б(— — 2.4?Пя.

Зубчатое колесо с косыми зубьями изо­бражено на рис. 261. Этот чертеж отлича­ет то, что в таблице параметров приведен модуль нормальной угол наклона зуба р, направление зуба, толщина зуба по хорде в нормальном сечении 5м, ход вин­товой линии Р<.

Контрольные вопросы

!. Что такое модуль зубчатого колеса? В ка­ких единицах он выражается?

2. Чему обычно равна высота головки зуба? высота ножки зуба?

3. Как называют три окружности, с помощью которых условно изображают зубчатый венец? Какими линиями их проводят на виде, перпен­дикулярном оси колеса?

4. Как изображают зубья зубчатого колеса в разрезе?

5. Какой из трех расчетных размеров диамет­ров окружностей нужно наносить на рабочих чертежах?

 

6. Какие основные сведения о зубчатом коле­се можно узнать из таблицы параметров?

7. Где располагают обозначения шерохова­тости рабочих поверхностей зубьев? вершин зубьев? впадин зубьев?

8. Как определить модуль, имея зубчатое колесо?

9. Почему после определения модуля нуж)№ сравнивать полученную величину со стандарт­ным значением для модулей?

Ю. Чем отличается чертеж прямозубого ци­линдрического колеса от косозубого?

Уярюжжемме 7/. Подсчитайте основные раз­меры цилиндрического прямозубого колеса с числом зубьев 80 и модулем 2 (с числом зубьев 90 и модулем 3).

Упражнение 72. Вычертите чертеж цилин­дрического зубчатого колеса с прямыми зубь­ями по ■ следующему его описанию. Модуль 2, число зубьев 42. Исходная форма колеса пред­ставляет собой цилиндр с отверстием для вала (без шпоночной канавки), края зубьев срезаны фасками)Х45°. Шероховатость рабочих повер­хностей зубьев Да),6, а поверхностей выступов и впадин зубьев Йа3,2.

Упражнение 73. Выполните эскиз с натуры цилиндрического зубчатого колеса.

Упражнение 74. На рис. 265 дана часть глав­ного вида цилиндрического прямозубого зубча­того колеса и неполный вид слева. Модуль /я = =4; число зубьев 2 = 32. Дочертите главное изображение, сделав его фронтальным разре­зом. Подсчитайте и нанесите на чертеж размер диаметра окружности вершин Нанесите обозначения шероховатости поверхностей; ра­бочие поверхности зубьев #а),6, поверхности вершин и впадин зубьев ДаЗ,2. Фаски имеют размер 2X45°.

§ 63. ЧЕРТЕЖИ КОНИЧЕСКИХ

ЗУБЧАТЫХ КОЛЕС

Конические зубчатые колеса (см. рис. 259, как и цилиндрические, вычерчи­

ваются условно (рис. 266). При этом об­щие правила выполнения чертежей цилин­дрических зубчатых колес, изложенные в предыдущем параграфе, действуют и в случае вычерчивания конических пря­мозубых колес. Размеры элементов этих колес подсчитывают по тем же формулам, что и для цилиндрических колес. Однако диаметры, модуль, высота головки и нож­ки зуба конического зубчатого колеса пе­ременны (рис. 266). Поэтому за диаметр делительной окружности принимают мак­симальное его значение. Значение модуля при подсчетах также берут наибольшее (на внешнем дополнительном конусе).

ГОСТ 19325—73 устанавливает, что ос­новой для подсчета размеров конических прямозубых колес является делитель­ный конус. По вершинам зубьев проходит конус вершин, а по впадинам зубьев — конус впадин. Кроме того, могут быть два дополни­тельных делительных конуса — внешний и внутренний. Образующие этих конусов расположены под прямым углом к об­разующей делительного конуса.

Для выполнения чертежа конического прямозубого колеса нужно знать внешний окружной модуль?п,,, число зубьев шестер-

Внешний дополнительный дели-

Рис. 266. Элементы конического зубчатого ко­леса

 

ни 2. Если рассматриваются два зубчатых колеса, находящихся в зацеплении, то чис­ла зубьев обозначаются соответственно X] и 2:.

В данном примере эти величины взяты следующие: т,=3 мм; 3)=20 (шестер­ни); 2: = 40 (колеса); диаметр вала ^Л = =20 мм.

Прежде чем приступить к вычерчива­нию, нужно подсчитать основные парамет­ры колеса.

. Диаметр делительной окружности коле- 'са определяем по формуле <%: = т,2:. В данном примере %: = 3-40 =!20 мм. Вы­сота головки зуба Ад берется равной моду­лю (внешнему): А. = /п, = 3 мм.

Высота ножки зуба берется равной 1,2 модуля: А/ = 1,2т.=!,2-3=3,6 мм.

Диаметр делительной окружности шес­терни (составляющей пару с изображае­мым колесом) <%) =?п,:) = 3-20 = 60 мм. После подсчета основных параметров приступают к вычерчиванию фронталь­ного разреза колеса. Построение вы­полняют в такой последовательности (рис. 267).

Вычерчивают два делительных конуса с общей образующей (рис. 267, а). Конус большего диаметра (а!й=120 мм) принад­лежит колесу меньшего диаметра (Л)= ==60 мм) — шестерне. К основанию дели­тельного конуса колеса проводят две ли­нии, расположенные под прямым углом к образующим конуса. В результате по­лучают внешний дополнительный конус колеса.

Вдоль образующей этого дополнитель­ного конуса откладывают от точки пере­сечения ееЛ с образующей делительного конуса размер высоты головки (в на­шем примере 3 мм) и размер высоты ножки А/ зуба, проводят через полу­ченную точку прямую ПОД углом 8а (угол конуса вершин), получая конус вершин (рис. 267, б). Отложив размер высоты ножки зуба (в нашем примере 3,6 мм) вдоль образующей дополнительного ко­нуса, соединяют полученную точку с вершиной делительного конуса, получая конус впадин колеса.

По образующей делительного конуса колеса откладывают размер длины зуба Ь, который можно подсчитать по соотноше­нию Ь = ' (6-г-8)?п,. приведенному в табл. 6. В нашем примере возьмем ко­эффициент равным 6 (колесо стальное), получим А = 6/я, = 6-3= 18 мм.

Определяют толщину обода венца и из соотношения, приведенного в табл. 6: я а; ж(2,5-т-'4)т,.

Для стального колеса берем коэффици­ент 2,5. Получаем п = 2,5т,= 2,5-3 = = 7,5 мм. Откладываем этот размер вдоль образующей дополнительного конуса и проводим вертикальную линию (рис. 267, а).

Делительный конус

Дополнительный средний Целительный конус

Рис. 267. Последовательность вычерчивания конического зубчатого колеса

По соотношениям, приведенным в табл. 6, подсчитываем диаметр Л и длину сту­пицы колеса, вычерчивая ее по этим раз­мерам (рис. 267, е). Показывают в ступи­це отверстие для вала, диаметр которого %, = 20 мм.

Вычерчивают вид слева колеса.

В соответствии с ГОСТ 2.402—68 на нем показывают для конических колес лишь две окружности зубчатого венца: окружность вершин зубьев — сплошной основной линией и делительную окруж­ность — штрихпунктирной тонкой линией (рис. 267, а).

В соответствии с ГОСТ 2.405—75 на рабочих чертежах конических зубчатых колес часть размеров проставляют на изо­бражениях, а часть — в таблице парамет­ров (рис. 268).

щ щи

На изображениях наносят диаметр большего основания конуса вершин (внешний диаметр вершин зубьев). На рис. 268 этот размер равен 79,3 мм. Про­ставляют размер от базовой поверхности (торца ступицы) до большего основания конуса вершин (размер 2!,64 мм). Указы­вают размеры двух углов: угол конуса вершин (угол 27° 22' на рис. 268) и угол внешнего дополнительного конуса (угол 65° 46'). Если зубчатое колесо имеет внешний дополнительный конус, то указы­вают ширину зубчатого венца (размер 26 мм). Всегда указывают размер базово­го расстояния, т. е. размер между верши­ной делительного конуса и базовой плос­костью, измеренный по геометрической оси колеса (размер 100-о.:з мм на рис. 268). Указывают размеры фасок или радиусы скруглений на кромках зубьёв.,

В таблицу параметров вносят помимо модуля число и тип зубьев, угол делитель­ного конуса 6 (угол 24° 13'40") и угол конуса впадин 6? (угол 21° 66'). Сведения о типе зубьев помешают в таблице пара­метров, потому что кроме прямых могут быть косые и круговые зубья с эвольвент- ными и другими профилями.

Во второй части таблицы параметров помещают данные для контроля колеса, а в третьей — справочные данные.

На соответствующих изображениях на­носят обозначения шероховатости рабочих поверхностей зубьев и поверхностей вер­шин и впадин. Кроме того, указывают предельные отклонения формы и располо­жения поверхностей.

Из рис. 268 видно, что вершины дели­тельного конуса и конуса вершин не со-

 

Ххххххххххххх

 

УМ
бяешной окружной jm / jm	т{
УмаммЛе[11]	г	л?
Тип зуба	-	Прямой
Исходный контур	-Я	ПИЯМ
им ймджммюм ямугд	ТГ	ж*з'м!
коэффициент смещения	if	й
у;м мяум ДляЛЛи	*f	VW
Степень точности		м-и-х
толщина зуба по хорве	s
бысота до горды	ht	2.W
Обозначение чертежа сопряженного колеса

1* Размер для справок: 2. Неуказанные предельные отклонения размеров: HI4; h/4; ±~2~-

Колесо зубчатое /ГЙНТАИ? бммЯУ /ИГГД7Д7- ж

ММ.МММ.МЛ чи—иуд

 

Рис. 268. Чертеж конического зубчатого колеса

впадают. Смещение их обеспечивает зазор постоянной величины по всей длине зубьев сопряженных колес, что делает передачу более плавной. На учебных чертежах этот зазор допускается не показывать.

Контрольные вопросы

). Какой модуль используют при подсчетах основных параметров конических зубчатых ко­лес?

2. Как называют конусы, которые встречают­ся при изображении конических колёс?

3. Что общего в изображении конических и цилиндрических зубчатых колес? Заштрихо­вывают ли зубья в продольных разрезах?

4. Под каким углом к делительному конусу расположен внешний дополнительный конус? внутренний?

5. Какие основные размеры указывают на изображениях конических зубчатых колес, а ка­кие — в таблице параметров?

Упражнение 75. Подсчитайте основные раз­меры конического прямозубого колеса, если мо­дуль равен 2,5, а число зубьев 60. Шестерня, сопряженная с этим колесом, имеет 30 зубьев.

Улрджнемме 76. Начертите прямозубое кони­ческое зубчатое колесо такой же конструкции, как на рис. 267. Модуль равен 3. число зубьев 32. Сопряженная шестерня имеет)8 зубьев.

$ 64. ЧЕРТЕЖИ ЧЕРВЯЧНЫХ КОЛЕС И ЧЕРВЯЧНЫХ ВИНТОВ

Червячные передачи служат для пере­дачи вращения между скрещивающимися валами (обычно под прямым углом) и со­стоят из червяка и червячного колеса (рис. 259, з). Они позволяют получать большие передаточные числа, плавность зацепления, бесшумны в работе.

Ведущим обычно является червяк. Вычерчивание червячного винта. Червяк представляет собой винт с резьбой, наре­занной на цилиндрической (рис. 269, а) поверхности или глобоиде (рис. 269,6). Червяки, резьба которых нарезана на ци­линдре, подразделяются на конволютные (2М), эвольвентные (2У) и архимедовы (2.4). Тип червяка определяется видом винтовой поверхности. У конволютных червяков теоретический торцовый профиль витка является удлиненной или укорочен­ной эвольвентой, у эвольвентных червя­ков — эвольвентой окружности, а у архи-

Рис. 269. Червячные передачи: а — с цилиндрическим червяком, б — с глобоид- ным червяком

 

медовых — спиралью Архимеда. Наиболее распространены архимедовы червяки вви­ду простоты их изготовления.

Элементы червяка аналогичны элемен­там резьбы. Червяки подразделяются на правые и левые (в зависимости от направ­ления винтовой линии) и по числу захо­дов.

Чертеж архимедова цилиндрического червяка представлен на рис. 270. На глав­ном изображении обычно выполняют мест­ный разрез, чтобы показать профиль вит­ка. Образующие цилиндра впадин изобра­жают сплошными тонкими линиями. На поперечном разрезе заштриховывают только сечение стержня'витка, а сечение винтового выступа не заштриховывают.

Диаметр делительной окружности чер­вяка подсчитывают по формуле где?и — модуль, а <7 — коэффициент диа­метра червяка, зависящий от заданной величины модуля (эта величина стандар­тизована).

Диаметр вершин витков червяка опре­деляют по формуле <%<,[=4)+2А,н=%) + + 2?я, где Аа) — высота головки, а диа­метр витка червяка впадин — по формуле ф]=%, —2,4гп, так как высота головки (А„]) равна модулю?п, а высота ножки Ар равна ],2 модуля.

Из расчетных размеров на рабочих чер­тежах червяков проставляют: диаметр ци­линдра выступов (размер 072-0.046 мм на рис. 270); длину нарезанной части (раз­мер 90-о.а7 мм); радиус закруглений вит­ков (Д = 0,3 мм и Д = 1,2 мм). Остальные данные указывают в таблице параметров. На рис. 270 модуль равен 6 мм, число

VM
Модуль	т	6
число витков		2
?у<? червяка	-	//)
ЛМЛЛ7АУАМ7<У /7й7д<?мб	Г	/Г
Направление линии Витка	-	/7лС<?0Р
Исходный	УР/ЙЯ/Г	—	ГОСТ19036-88
<Г/77Л/7ЛА /77луул/77<у	-	лЛ7. 7-/
>С7/70л%%о!М^ %ИЯММЙ	1 ММ Ял0фл/7Я	а.	2С°
л/ГС/77С л/77/Г	С	'12
,%а?М?АМ1	м/й луД</н?а/&	d,	70 -0,043
Ход витка	Лг/	ДД

ХХУ'ХХХХ ХУХХХХ

Рабочий профиль 2 а 45'

2 фаски

гШШШ f А

 

Неуказанные предельные отклонения размеров: ни, h

Д<МХ.ДХ ХШ.ХХХ

 

/7йЯ7. лД М<МГДМ7С%

Червяк архимедоб

Тм"м1 Дсл7А

/?йс<д! /?лГ/77М

ТЛ

 

л<м<м' "УШГ

5"

Гл7л4л /ЙГ7*Д7Д7-<!

 

Рис. 270. Чертеж архимедова цилиидрического червяка — 160 —

Рис. 27]. Вычерчивание червячного колеса

 

заходов 2, тип червяка архимедов, направ­ление витка правое.

Вычерчивание червячного колеса. Рас чет. основных параметров и вычерчивание зависят от размеров, червяка.

Общие правила выполнения чертежей те же, что,для вычерчивания цилиндрических зубчатых колес. То же/ можно сказать о подсчетах основных параметров.

Их определяют но следующим форму - лам (в расчетах применяют модуль./п).

Диаметр делительной окружности ко леса d2=m-z-2, где 22—число зубьев колеса.

Диаметр окружности вершин колеса' 4%а2 = %%2"}"2?П.

Диаметр окружности впадин колеса %Я=%2—2,4т.

Высота головки зуба Аа: =?п. Высота ножки зуба колеса Ар =1,2.

Кольцевую канавку, вытачиваемую на ободе червячного колеса, описывают на чертеже из центра червяка (рис. 271, а). ■ Чтобы найти этот центр на чертеже, нуж­но определить Межосевое расстояние (рас­стояние между центрами колеса и червя­ка), которое равно полусумме диаметров делительных окружностей колеса и червя­ка, т. е. а„=(%)+*%:)/2.

Этот размер с предельными отклонения - ми помещают в таблице параметров и ис­пользуют при нарезании зубьев. Его назы - вают межосевым расстоянием в обработке.

При вычерчивании фронтального разре­за проводят осевые линии: горизонталь­ную — отверстия для вала и вертикаль­ную -еимметрии колеса. На ней находит­ся центр червяка, сопряженного с коле­сом. От центра колеса вдоль этой линии и откладывают межосевое расстояние а, (рис. 27)). Из полученной точки проводят окружность, диаметр которой равен диа­метру делительной окружности червяка й) (Л1 = <7-?п). Затем от точки встречи этой окружности с вертикальной осью колеса откладывают вдоль нее высоту головки зуба Ла(Ла = т) и высоту Ножки зуба А, (Ау=!,2/п). На.рис. 271,а эти построе­ния выделены цветом. Через полученные точки очерчивают дуги, концентричные де­лительной окружности. Такие же построе­ния щьгцолняют с противоположной сторо­ны колеса. Полученные тфким образом изображения зубьев в разрезе не заштри­ховывают, как и иа чертежах цилиндриче­ских и конических колес, а делительную окружность обводят штрихпунИтириой ли­нией (рис. 271,6).

На виде слева зубчатый венец показы­вают лишь двумя окружностями: дели­тельной и наибольшей вершин зубьев (на­ружный диаметр колеса). Окружность впадин не показывают (как и у конических зубчатых колес). Далее вычерчивают от­верстие для вала, диаметр которого выби­рают, как и для других колес, в соответст­вии с ГОСТ 6636 69. Размеры остальных элементов колеса определяют из соотно­шений, данных в табл. 6.

На рис. 272 приведен чертеж червячного колеса, сопрягаемого с архимедовым чер­вяком.

В соответствии с ГОСТ 2.406—76 на рабочих чертежах червячных колес указы­вают диаметр окружности вершин в сред­ней плоскости зубчатого венца (размер 0 272 мм на рис. 272), наибольший диал метр зубчатого венца, (размер, 0281 мм), ширину зубчатого вечна (размер 54 мм), расстояние от средней плоскости, зубчато­го венца до базового торца (размер 27 мм), данные, определяющие внешний контур зубчатого венца, например радиус обточки поверхности выступом (раз­мер л?24), размеры фрсок и т. п., ше­роховатость боковых поверхностей зубьев.

В таблице параметров наряду с данны­ми о модуле и числе зубьев (6 и 44) приво­дят сведения о сопряженном червяке (тип червяка, число витков, направление линии витка), межосевом расстоянии а* (размер, 160 мм) и др.

 

— 161 —

6 Техническое черчение

 

Рис. 272. Чертеж червячного колеса, сопряженного с архимедовым червяком

—!62—

Контрольные вопросы

). Что общего н изображении в разрезе зубь­ев червячных и цилиндрических зубчатых ко­лес!? '•''■'

2. Какие окружности проводят при изобра­жении зубчатого венца червячного колеса на виде, ■ перпендикулярном оси колеса ' (на виде мена)?

3. Как определяется межосевое расстояние в Червячмой передаче?

: 4., Какой, модуль используется. при определе­ние, основных параметров червячных передач?

! $. Какую чаеТь червяка но заштриховывают на поперечном разрезе?

: ^ярв*«в*Мв-.7!!*.Рассмотрите рис. 2?2 и от- ле&те. на следующие врп[лбсы:

') Какое колесо изображено на чертеже?

! 2. Чему равен модуль?

$. Сколько зубьев.уЛколеса?

4. С каким типом червяка сопрягается это

КОЛЮЮ?"™;________________.:..:.........:..:.......-

! 5. Чему равно межосевое расстояние в обра­ботке?

6. Какова шероховатость рабочих поверхно­стей зубьев?

7. Какова шероховатость поверхностей вы­ступов зубьев? поверхностей впадин?

§ 65. ЧЕРТЕЖИ ЗУБЧАТЫХ РЕЕК

Наглядное изображение зацепления зубчатого колеса с рейкой показано на рис. 259, м. Зубчатую рейку можно рас­сматривать как развернутый в прямую Губчатый конец цилиндрического зубчато­го* колеса. (рис. 273), поэтому правила изображения се такие же, как и зубчатого колеса. Поверхности вершин зубьев вы­черчивают сплошной основной линией, де­лительные поверхности — штрихиунктир- ной, а поверхности впадин — сплошной тонкой линией. В разрезе зубья не заштри­ховывают, а на месте делительной повер- хностипроводят шт])ихпунктирную линию.

Все расчетные размеры у рейки, находя­щейся в ладеплении с зубчатым колесом, равны соответствующим размерам колеса, т. е. модуль, высота готовки и ножки зуба у них одинаковы.

Согласно ГОСТ 2л64—75 на рабочих чертежах зубчатых реек (рис. 274) указы­вают: ширину зубчатой части плоской рей­ки (размер 30), высоту зубчатой рейки (размер 24), длину нарезанной части рей­ки (размер 180 мм. этот размер указыва­ют по делительной поверхности), направ-

Рис. 273. Зубчатая рейка

 

ление наклона и угол наклона зубьев (ес­ли рейка с косыми зубьями). Рейка, изображенная на рис. 274, имеет прямые зубья.. Указывают также шероховатость боковых поверхностей зубьев, поверхности выступов и поверхности впадин, размеры фасок или радиусы закруглений на кром ках вершин зубьев. При необходимости показывают рабочий профиль зубьев

Данные, характеризующие нарезанную часть рейки, помещают в таблице пара метров.

Контрольные воп р о с ы

1. Как вычерчивают в разрезе зубья рейки, если секущая плоскость проходит вдоль них?

2. Какими линиями показывают на виде спе реди поверхность вершин? поверхность впадин?

3. Чему равны высота головки и высота нож­ки зуба рейки, еели у сопряженного колеса они равны соответственно 3 и 3.6 мм?