В.Г. БУСЫГИН
Методические указания для бакалавров
по дисциплинам
«Прикладная механика», «Строительная механика»
Барнаул 2013
ВВЕДЕНИЕ
Определение опорных реакций балок и рам является начальным и важнейшим этапом расчета статически определимых систем на прочность и жесткость. Несмотря на простоту алгоритма расчета, многие студенты, впервые решая подобные задачи, не могут получить правильный числовой ответ. Причин неудовлетворительного результата может быть несколько:
- слабое знание или непонимание теоретического материала по разделу «Статика»;
- отсутствие практических навыков решения задач;
- неумение сконцентрировать внимание на решаемой задаче при записи уравнений, а также при выполнении арифметических вычислений.
Следует отметить, что задачи по рассматриваемой теме являются простейшими в прикладной механике. Опытный расчетчик часто может решить подобную задачу в «уме», даже не используя калькулятор (при целочисленных исходных данных). Так что, неудовлетворительная оценка свидетельствует лишь о нежелании студента освоить данную тему.
Контрольная работа по определению опорных реакций балок для студентов направления «Приборостроение» является первой контрольной точкой, по результатам которой можно судить о степени освоения начальных разделов курса «Прикладная механика». Работа проводится на практических занятиях на 5-й неделе семестра.
Студенты направления «Архитектура» и «Дизайн архитектурной среды», изучающие «Строительную механику», выполняют расчетное задание, начальным этапом которого является также определение опорных реакций балок.
Цель методических указаний – способствовать закреплению основных понятий статики и подготовиться к изучению сопротивления материалов. Для этого в данной работе приведен весь необходимый теоретический материал и даны примеры расчетов.
Задания на контрольной работе формулируются для простых балок. К простым балкам относятся балки, опирающиеся на две шарнирные опоры и балки, защемленные одним концом (консольные балки). Простые балки являются статически определимыми, т.е. для определения опорных реакций и внутренних усилий достаточно использовать лишь уравнения статики. Размеры балки, схема опирания и величины нагрузок задаются преподавателем. Требуется определить опорные реакции балки, используя три уравнения равновесия.
На изучение материала и подготовку к контрольной работе по рабочему плану дисциплины «Прикладная механика» отводится 20 часов.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К КОНТРОЛЬНОЙ РАБОТЕ
Формирование навыков решения задач по механике надо начинать с изучения теоретического материала, а именно – раздела «Статика». Необходимо изучить следующие вопросы:
- основополагающие понятия теоретической механики (классификация сил, внешние и внутренние силы, связи, активные и реактивные силы);
- определения различных систем сил (уравновешенной, сходящейся, плоской, пространственной, распределенной);
- виды опор балок;
- аксиомы статики;
- проекция силы на ось;
- момент сосредоточенной силы относительно точки;
- момент равномерно распределенной нагрузки относительно точки (в плоском случае);
- уравнения равновесия для определения опорных реакций простой двухопорной балки;
- уравнения равновесия для определения опорных реакций защемленной консольной балки.
Определение реакций опор является базовым навыком расчета практически любой статически определимой конструкции. Ниже приведены основные понятия статики.
ОСНОВНЫЕ ПОНЯТИЯ СТАТИКИ
Понятие силы и системы сил
Статика - раздел теоретической механики, в котором изучают свойства сил, условия их одновременного действия на тело и условия равновесия тел под действием этих сил.
Все тела в природе взаимодействуют друг с другом. Мерой механического взаимодействия служит особая физическая величина – сила. В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Силы, характеризующие взаимодействие одного тела на другое, называют внешними, а силы, характеризующие взаимодействие частиц (частей) данного тела между собой, - внутренними. Силы (нагрузки), действующие на тела, в зависимости от условий их приложения могут быть поверхностными и объемными.
Сила – величина векторная. Для ее характеристики необходимо знать численное значение, направление действия и точку приложения к телу. Например, будем прикладывать к стулу одну и ту же по модулю силу F. При приложении силы сверху вниз стул остается в состоянии покоя; при положении силы снизу вверх – стул поднимается; изменим направление нагружения, приложим силу горизонтально к спинке стула – стул опрокинется. Так как во всех случаях направление и место приложения силы различны, то и результат действия силы на стул разный, несмотря на то, что модуль силы F во всех случаях одинаков. Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.
Скалярная величина (например, температура) характеризуется только величиной и координатами точки, в которой эта величина рассматривается.
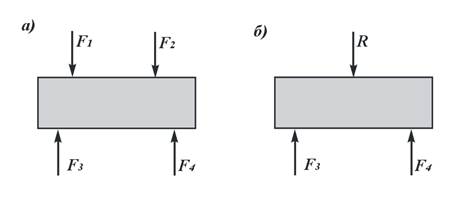
Рисунок 1 – Система сил:
а – заданная система сил; б – эквивалентная система сил
Совокупность сил, действующих на тело, называется системой сил. Если под действием сил тело остается в покое или движется равномерно и прямолинейно по отношению к другим телам, то такое состояние тела называется равновесием. Равновесие возможно в том случае, если система сил, действующих на тело, уравновешена. Такую систему сил называют равновесной (уравновешенной) или эквивалентной нулю. Системы сил называются эквивалентными, если их действие на тело одинаково. Например, если системы сил, изображенных на рис. 1, а и рис.1, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.
Так как система сил F1 и F2 эквивалентна одной силе R (рис. 1, б), то сила R называется равнодействующей данной системы сил. Силы F 1 и F2 в свою очередь могут называться составляющими силы R.
Изучая действие силы на тело (например, на балку, ферму, колонну и т. п.), можно не учитывать его деформации, т. е. изменения формы и размеров, так как они очень малы по сравнению с размерами самого тела. Поэтому в статике пользуются такими абстрактными понятиями, как абсолютно твердое тело и материальная точка. Абсолютно твердым телом называют такое тело, которое под действием нагрузки не меняет своей формы, т. е. не деформируется. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.