На рис. 18 изображена система сил, действующих в плоскости YOZ. Начало координат (точка О) в плоскости действия сил может быть выбрана произвольно. Тогда проекции всех сил на ось OX равны нулю, так как силы перпендикулярны оси ОХ и моменты всех сил относительно осей OY и OZ также равны нулю, потому что эти оси и силы лежат в одной плоскости.

Рисунок 18 – Произвольная плоская
система сил
В курсе теоретической механики доказывается, что для равновесия произвольной плоской системы сил необходимо и достаточно составление трех независимых уравнений:
 (1)
(1)
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из двух координатных осей, лежащих в плоскости этих сил, равнялась нулю, и сумма моментов всех сил относительно произвольной точки в плоскости этих сил также равнялась нулю.
Для плоской системы сил, кроме уравнений (1), уравнения равновесия можно составлять в следующих формах:
 (2)
(2)
или
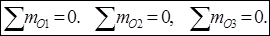 (3)
(3)
В уравнениях (2) точки о1, о2 не должны лежать на перпендикуляре к оси OY, на которую выполняется проецирование сил. Например, если точки о1, о2 выбрать на оси ОZ, то из двух последних уравнений в (2) вытекает первое уравнение.
Для независимости уравнений (3) точки о1, о2, о3 не должны лежать на одной прямой в плоскости действия сил.
Данные условия равновесия широко используются при расчете плоских изгибаемых элементов (балок, рам) в строительных конструкциях. При расчете можно пользоваться любой из трех форм уравнений равновесия (1), (2), (3), исходя из конкретных условий.
Система параллельных сил, расположенных в одной плоскости
Данная система сил является частным случаем рассмотренной выше произвольной плоской системы сил. Она очень часто встречается в расчетах конструкций, так как обычно силами F являются силы тяжести, т.е. вертикальные, а следовательно, и параллельные силы.
Согласно рис. 19, все силы параллельны и лежат в плоскости YOZ, причем они перпендикулярны оси OZ. Тогда проекция всех сил на ось OZ равна нулю, соответствующее уравнений проекций превращается в тождество, и из условий равновесия (1) остаются два условия:
 (4)
(4)
или, используя (2),
 (5)
(5)
Точка oi в (4) – произвольная точка плоскости действия сил. В уравнениях (5)
точки о1 и о2 нельзя выбирать на прямой, параллельной силам. При решении задач эти точки обычно выбирают на оси OZ, что позволяет первое из уравнений (2) использовать для проверки правильности расчетов.
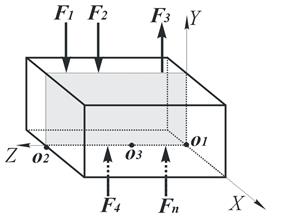
Рисунок 19 – Система параллельных сил, расположенных в одной плоскости
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма величин всех сил равнялась нулю и сумма моментов всех сил относительно любой точки в плоскости этих сил также равнялась нулю.
Вопросы для самопроверки
1. Что такое абсолютно твердое тело?
2. Какие величины называются векторными и какие – скалярными?
3. Что такое сила и какова ее размерность?
4. Что называется моментом силы относительно данной точки и какова его размерность?
5. Что называется реакциями связей?
6. Что такое статически эквивалентная система сил?
7. Что такое аксиомы статики твердого тела? Как они формулируются?
8. Какая система сил называется сходящейся? Как определить их равнодействующую?
9. Что называется главным вектором плоской системы сил?
10. Составьте условия равновесия для произвольной плоской системы сил.
11. Составьте условия равновесия для системы сходящихся сил.
12. Составьте условия равновесия для плоской системы параллельных сил.