Аксиомы статики выражают основные свойства сил, действующих на тело. Большинство аксиом статики является следствием основных законов механики, полученных как обобщение опыта. Так, закон инерции нашел свое отражение в условиях равновесия твердого тела. Их можно получить, решая вопрос о частном случае движения твердого тела – состоянии покоя.
Принцип независимости действия сил. Если на материальную точку (твердое тело) действуют одновременно несколько сил, то каждая из этих сил действует независимо от других. Иначе, эффект совместного действия нескольких сил, равен сумме эффектов действия каждой силы в отдельности. Следствием этого принципа механики является аксиома параллелограмма сил (аксиома III).

Рисунок 2 – Силы лежащие на одной прямой:
а - действие двух равных и противоположно направленных сил;
б – перенос силы по линии ее действия
Аксиома I. Если на абсолютно твердое тело действуют две равные и противоположные по направлению силы, лежащие на одной прямой, то они уравновешивают друг друга (рис. 2, а).
Аксиома II. Действие системы сил на абсолютно твердое тело не изменится, если к ней прибавить или отнять от нее любую уравновешенную систему сил.
Следствие из аксиом I и II. Действие силы на твердое тело не изменится, если эту силу перенести по линии ее действия в любую точку тела.
Пусть на тело в точке А действует сила F (рис. 2, б). Приложим к телу по линии действия силы F в точке В две уравновешенные силы F1 и F2, равные по модулю½ F ½. Система трех сил F, F1 и F2 будет эквивалентна либо силе F, либо силе F1 (так как сила F1=F и F2=-F, то систему уравновешенных сил F2, F можно не учитывать). В результате в точке В на тело будет действовать сила F1=F, что равносильно переносу силы F из точки А в точку В.
Аксиома III. Две силы, действующие на тело в одной точке, имеют равнодействующую в той же точке, изображаемую вектором, представляющим собой диагональ параллелограмма, построенного на векторах этих сил, как на сторонах.
Равнодействующую R (рис. 3) сил F1 и F2 называют геометрической суммой слагаемых векторов F1 + F2 = R. Следует отличать векторную сумму от скалярной суммы (алгебраической). Следовательно, аксиому III можно сформулировать так: равнодействующая двух сил, действующих на одно тело в одной точке, равна геометрической (векторной) сумме этих сил и приложена в той же точке тела. Данная аксиома выражает правило параллелограмма сил.
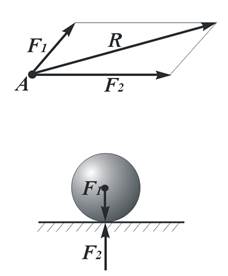
Рисунок 3 – Равнодействующая
двух сил, выходящих из одной точки
Рисунок 4 – Принцип противодействия
Аксиома IV (принцип противодействия). При всяком действии одного материального тела на другое возникает равное по величине и противоположное по направлению противодействие: F2 = - F1 (рис. 4). Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме IV рассматривается случай, когда силы приложены к разным телам, и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме II.
Этот принцип утверждает, что в природе не существует односторонних явлений. На рис. 5 изображена балка, опирающаяся на стены концами А и В. Для выявления сил действия и противодействия отделим балку от стен. Тогда силы действия балки на стену выражаются силами DA и DB , приложенными к стенам, а силы противодействия – силами RA и RB, приложенными к балке, которые в дальнейшем будем называть реакциями.
. 
Рисунок 5 – Опирание балки на опоры:
а – схема загружения балки; б – силы действия балки
на опоры и противодействия со стороны опор на балку
Аксиома V (принцип отвердения). Равновесие деформируемого тела, находящегося под действием системы сил, не нарушится, если под нагрузкой тело станет абсолютно твердым. Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.
Аксиома VI(аксиома связей ). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме – в следующем параграфе).
Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.
Связи и реакции связей
Тело называется свободным, если оно может перемещаться в любом направлении, например воздушный шар в потоке воздуха. Обычно движение тел в пространстве ограничено. Такие тела называются несвободными.
Любое тело, ограничивающее свободу передвижения другого тела, называют связью. Используя аксиому связей, всякое несвободное тело можно рассматривать как свободное, если действие связей заменить силами – реакциями связей.
Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим, активным силам.
Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровая нагрузки и т. п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.
Одна из главных задач статики твердого тела – нахождение реакции связей. Для определения реакции связей необходимо найти величину этой реакции, линию и направление ее действия. Линия действия реакции обычно проходит через точку касания тела и связи. Численное значение реакции определяется расчетом, а направление реакции зависит от вида (конструкции) связи.
Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.
Рассмотрим основные типы связей, используемых в качестве опорных элементов или для соединения элементов сооружений в пространстве.
Свободное (незакрепленное) опирание тел на поверхность или точку опоры (рис. 6, а, б). Гладкая поверхность или точка опоры препятствуют перемещению тел только по направлению перпендикуляра, восстановленного из точек опоры к этой плоскости. Реакция в этих случаях направлена по нормали (перпендикуляру) к опирающейся поверхности.
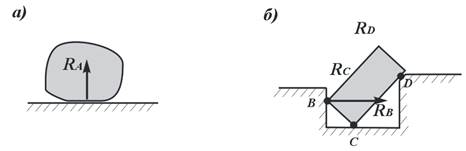
Рисунок 6 – Свободное незакрепленное опирание тел:
а – на поверхность; б – на точки опорных элементов
Гибкие связи (рисунок 7, а, б). Под гибкими связями подразумевают тросы, нити, цепи, веревки и т. п. Перемещение тела от точки подвеса ограничено гибкой нерастяжимой нитью. Такая связь может воспринимать только растягивающие усилия. Реакции гибких связей направлены вдоль нити к точке ее прикрепления.

Рисунок 7 – Гибкие связи: а – подвеска груза с помощью троса;
б – фиксация груза с помощью двух тросов
Связь в виде жесткого стержня, шарнирно закрепленного по концам (рис. 8, а, б). Такая связь препятствует перемещению тела по оси стержня. Реакция направлена вдоль оси этого стержня. В отличие от гибкой нерастяжимой нити, шарнирный стержень строго фиксирует расстояние между двумя точками по концам стержня, которые не могут сблизиться (сжатие) или удалиться (растяжение).
. 
Рисунок 8 – Связи в виде жесткого стержня:
а – стержень препятствует перемещению бруса вниз;
б – стержень препятствует перемещению бруса вверх
Шарнирно - подвижные опоры (рис. 9, а, б). Под шарниром подразумевают связь, допускающую вращение одного тела по отношению к другому. Одним из распространенных видов шарнирно-подвижных опор являются катковые опоры (катки). Связь препятствует движению тела по нормали к опорной поверхности катков.
Таким образом, в подвижной (катковой) опоре возникает одна опорная реакция, направленная перпендикулярно плоскости опорной поверхности аналогично опорной реакции в шарнирном жестком стержне. Конструктивное решение шарнирно-подвижных опор может быть весьма разнообразным. В строительной механике такую опору изображают в виде шарнирного стержня (рис. 9, б).
Шарнирно-неподвижная опора (рис. 10, а, б). Это устройство представляет собой опорный элемент (подшипник), внутри которого вращается палец (ось) шарнира. Такая опора не препятствует вращению вокруг оси, но препятствует движению тела в любом направлении в плоскости, перпендикулярной к оси шарнира.
Реакция R шарнирно-неподвижной опоры расположена в плоскости, перпендикулярной оси возможного вращения, и ее направление определяют две взаимно перпендикулярные составляющие Rx и Ry, соответствующие направлению выбранных осей (рис. 10, а).

| Рисунок 9 – Шарнирно подвижная опора: а – вид катковой опоры; б – расчетная схема шарнирно-подвижной опоры | Рисунок 10 – Шарнирно-неподвижная опора: а – вид шарнирно-неподвижной опоры; б, в – расчетные схемы шарнирно-неподвижных опор |
В строительной механике шарнирно-неподвижную опору изображают в виде двух шарнирных стержней пересекающихся в точке опоры (рис. 10, б) или шарнира (рис. 10, в).

Рисунок 11 – Жесткая заделка:
а – вид жесткой заделки; б – расчетная схема жесткой заделки
Жесткая заделка (рисунок 11, а, б). Это соединение исключает возможность каких-либо перемещений абсолютного твердого тела. Балка, изображенная на рис.11, а, жестко заделана в стену в точке А. Перемещению ее в вертикальном направлении, препятствует реакция Ry, перемещению в горизонтальном направлении препятствует реакция Rx и повороту вокруг точки А – опорный момент МА. Характерным для данной опоры является наличие опорного момента сил, исключающего вращение тела вокруг любой оси. Схематическое изображение такой опоры в строительной механике показано на рис. 11, б.
С помощью указанных опорных связей сооружения прикрепляются к фундаментам или отдельные элементы соединяются между собой.
Проекция силы на ось
Ввиду особой важности для решения задач статики напомним известное из курса векторной алгебры определение проекции вектора на ось, в нашем случае - вектора F.
Проекцией вектора F = AB (рис. 12) на ось m называют отрезок АmВm оси m, заключенный между двумя плоскостями, перпендикулярными оси m и проходящими через начало и конец вектора F. Точка Аm – начало проекции, точка Вm – конец проекции.
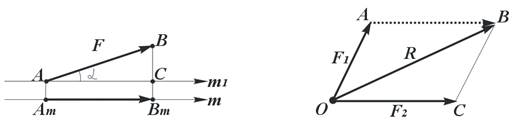
| Рисунок 12 – Проекция силы на ось | Рисунок 13 – Правило силового треугольника |
Если направление от начала проекции Аm к концу проекции Вm совпадает с положительным направлением оси, то величину проекции берут со знаком плюс, а в противоположном случае – со знаком минус. Данное определение справедливо при любых расположениях вектора F и оси m в пространстве. На рис. 12 проекция силы F на ось m – Fm положительна.
Проведем ось m1, параллельную оси m. Так как отрезок ААm= СВm, а плоскости I и II перпендикулярны оси m, то АС=АmВm=Fm. Следовательно, при определении проекции силы на ось можно силу или ось переносить параллельно так, чтобы получились пересекающиеся прямые, а силу считать приложенной в точке пересечения.
Величину проекции силы на ось при всех возможных положениях силы можно определить по единой формуле Fm=Fcosa, где a - угол между направлением вектора силы и оси m. В практических расчетах удобнее умножать модуль силы на косинус ее острого угла с осью, а знак величины проекции определять из чертежа.
Равнодействующую двух сил можно получить из правила силового треугольника. Из правила параллелограмма отрезок АВ (рис. 13) равен и параллелен отрезку ОС. Поэтому, если мысленно отложить вектор силы F2 от конца вектора силы F1 (точка А), то равнодействующая R имеет начало в точке О, а конец - в точке В. Получили правило силового треугольника.
Аналогично, чтобы сложить систему сил, приложенных в одной точке, необходимо от конца первой силы отложить вектор второй силы, от конца второй силы отложить вектор третьей силы и т. д. Вектор равнодействующей R имеет начало в начале первой силы и конец в конце последней. Вектор R, замыкающий силовой многоугольник, называют векторной суммой сил.
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил. Система сходящихся сил, действующих на абсолютно твердое тело, всегда может быть заменена одной сосредоточенной силой – равнодействующей, проходящей через точку пересечения линий действия этих сил. Такая равнодействующая называется главным вектором системы сходящихся сил.
Момент силы. Пара сил
Действие силы на тело характеризуется ее численным значением (модулем), линией действия и направлением. Кроме того, в случае закрепленного тела (в одной или в нескольких точках) вводится понятие момента силы относительно точки.

Рисунок 14 –
Момент силы F относительно точки О
Момент силы относительно точки характеризует вращающее действие силы относительно этой точки. Его определяют как произведение силы F на длину перпендикуляра h, опущенного из этой точки на линию действия силы (рис. 14). Длину этого перпендикуляра называют плечом. Формулу для момента силы можно записать так: Moi = Fi hi, где индекс о обозначает точку, относительно которой определяют момент силы (центр момента), h i – плечо силы F i.
Примем условно момент силы на рис. 15 положительным, если он стремится повернуть тело вокруг центра момента по ходу часовой стрелки, и отрицательным – против часовой стрелки. Тогда Mo1 = - F1h1, Mo2 =F2h2, Mo3 = 0. Момент силы F 3 относительно точки о (Мо3) равен нулю, так как линия действия данной силы пересекает точку о.
Пара сил – это две равные по абсолютному значению параллельные силы, направленные в противоположные стороны и имеющие разные линии действия (рис. 16). Плоскость, в которой действует пара сил, называется плоскостью пары. Пара сил не имеет равнодействующей и может быть заменена только другой эквивалентной парой сил. Сумма проекций сил, образующих пару, на любую ось равна нулю. Момент пары равен произведению одной из ее сил на плечо.
Пара сил также сообщает телу вращательное движение, как и момент силы относительно точки.

| Рисунок 15 – Момент сил F1, F2, F3 относительно точки о | Рисунок 16 – Эквивалентные пары сил |
Часто пару сил изображают в виде изогнутой стрелки с обозначением момента (рис. 16). Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.
Например, внутренние силы будут различны для балок, изображенных на рис.17, а, б.

Рисунок 17 – Замена пары сил сосредоточенным моментом:
а) вид изогнутой оси балки при нагружении двумя сосредоточенными силами;
б) вид изогнутой оси балки при нагружении сосредоточенным моментом